Определение. Дифференцируемая функция F(x) называется первообразной
для функции f(х) на интервале (а, b), если для любого
х Î (а, b) выполняется равенство: F'(x) = f(x).
Например:  , т. к.
, т. к. 
Из примера видно, что для данной функции существует множество первообразных.
Справедлива лемма о первообразных.
Лемма. Если F(x) – первообразная для функции f(х) на интервале (а, b), то всякая другая первообразная для функции f(х) отличается от F(х) на постоянное слагаемое, т.е. может быть представлена в виде F(х) + С, где С - постоянная.
Определение. Неопределённым интегралом от функции f(х) называется
множество всех её первообразных. Обозначение:  ,
,
где х – переменная интегрирования, f(х) – подынтегральная
функция, f(x)dx – подынтегральное выражение.
Таким образом,  .
.
Операция нахождения неопределённого интеграла называется интегрированием. Она позволяет по производной (или дифференциалу) какой-либо функции найти саму функцию.
Основные свойства неопределённого интеграла
1. Неопределённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов от слагаемых функций: 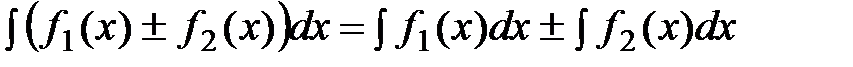 .
.
2. Постоянный множитель можно выносить за знак интеграла:
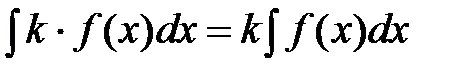 .
.
3. Производная от неопределённого интеграла равна подынтегральной функции (или дифференциал от неопределённого интеграла равен подынтегральному выражению):  (или
(или  ).
).
4. Неопределённый интеграл от дифференциала функции f(х) равен сумме этой функции и произвольной постоянной:  .
.
5. Вид формулы не изменится, если независимую переменную х заменить любой дифференцируемой функцией от х. Если 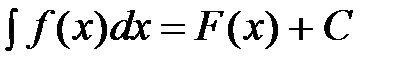 , то и
, то и  , где U = U(x) – функция, имеющая непрерывную производную.
, где U = U(x) – функция, имеющая непрерывную производную.
На основании определения неопределённого интеграла и его свойств можно записать следующую таблицу интервалов (таблица 9).
Таблица 9 - Таблица интегралов
| Название интеграла | Простые функции | № | Сложные функции 
|
| От дифференциала | 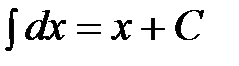
| 
| |
| От степенной функции |  , n - число , n - число
| 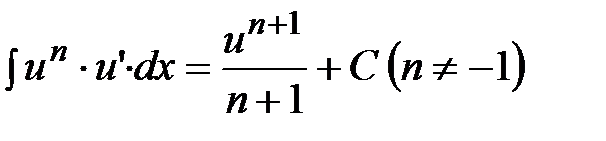
| |
| От показательной функции |  , а - число , а - число
| 
| |
| От экспоненты | 
| 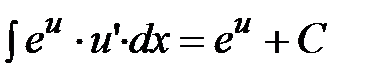
| |
| От синуса | 
| 
| |
| От косинуса | 
| 
| |
| От тангенса | 
| 
| |
| От котангенса | 
| 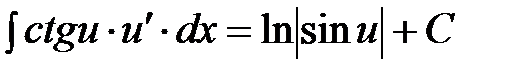
| |
| Интеграл, дающий тангенс | 
| 
| |
| Интеграл, дающий котангенс | 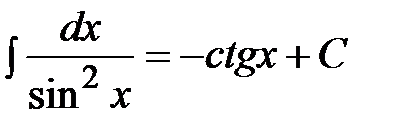
| 
| |
| Интегралы, применяемые к дробям, знаменатели которых находятся в первой степени | |||
| Интеграл, дающий логарифм знаменателя | 
| 
| |
| Интеграл, дающий арктангенс | 
| 
| |
| Интеграл, дающий «высокий логарифм» | 
| 
| |
| Интегралы, применяемые к дробям из знаменателя которых извлекается квадратный корень | |||
| Интеграл, равный удвоенному знаменателю | 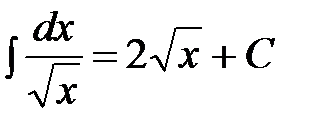
| 
| |
| Интеграл, дающий арксинус | 
| 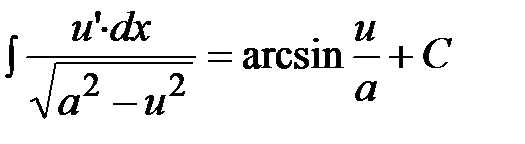
| |
| Интеграл, дающий «длинный логарифм» | 
| 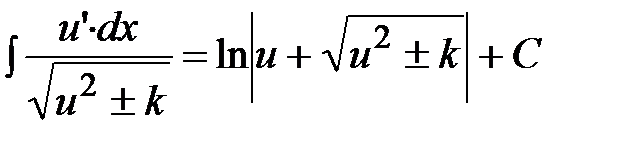
|
Методы интегрирования
Рассмотрим основные методы интегрирования: табличное интегрирование, интегрирование по частям, интегрирование методом замены переменной.
а) табличным интегрированием называется метод, при котором данный интеграл путем алгебраических, тригонометрических или других тождественных преобразований подынтегральной функции и применения свойств неопределённого интеграла приводится к одному или нескольким табличным интегралам.
Пример 53. Вычислить интегралы: а)  ; б)
; б) 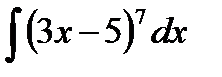 ; в)
; в)  ; г)
; г) 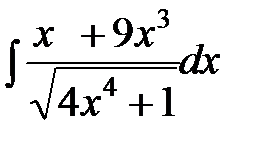 . Решение. а) Постоянный множитель вынесем за знак интеграла и найдём неопределённый интеграл от степенной функции хn:
. Решение. а) Постоянный множитель вынесем за знак интеграла и найдём неопределённый интеграл от степенной функции хn:
 .
.
б)Подынтегральная функция представляет собой сложную степенную функцию, интеграл от которой по формуле 2 таблицы интегралов должен содержать производную её основания u  , т.е. u' = 3. Умножим подынтегральное выражение на 3, а затем вынесем за знак интеграла множитель
, т.е. u' = 3. Умножим подынтегральное выражение на 3, а затем вынесем за знак интеграла множитель  , называемый «корректирующем» множителем. Эти рассуждения будем оформлять в квадратных скобках, стоящих после интеграла, т.е.:
, называемый «корректирующем» множителем. Эти рассуждения будем оформлять в квадратных скобках, стоящих после интеграла, т.е.:
 .
.
в) Раскрываем скобки, а затем применяем табличные интегралы 6 и 2:

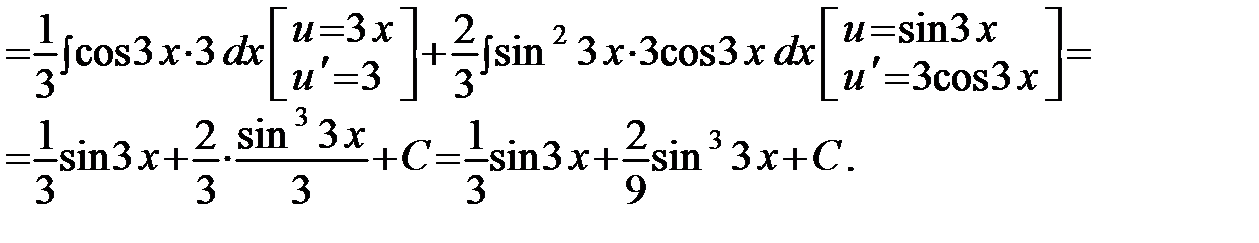
г)Разделим почленно числитель на знаменатель, и применим табличные интегралы 16,14:


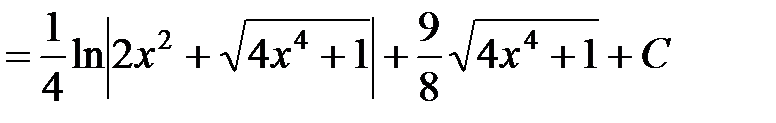 .
.
б) Интегрированием по частям называется метод нахождения интеграла по формуле:  , (8.1)
, (8.1)
где  - непрерывно дифференцируемые функции.
- непрерывно дифференцируемые функции.
Во многих случаях эта формула позволяет перейти от более сложного интеграла 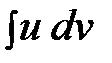 к более простому
к более простому  . При этом u называют дифференцируемым множителем, т. к. в процессе применения формулы его приходится дифференцировать; по той же причине
. При этом u называют дифференцируемым множителем, т. к. в процессе применения формулы его приходится дифференцировать; по той же причине  называют интегрируемым множителем. При этом за u берется такая функция, которая при дифференцировании упрощается, а за
называют интегрируемым множителем. При этом за u берется такая функция, которая при дифференцировании упрощается, а за 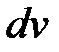 - та часть подынтегрального выражения, интеграл от которой во многих случаях является или сводится к табличному.
- та часть подынтегрального выражения, интеграл от которой во многих случаях является или сводится к табличному.
 Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
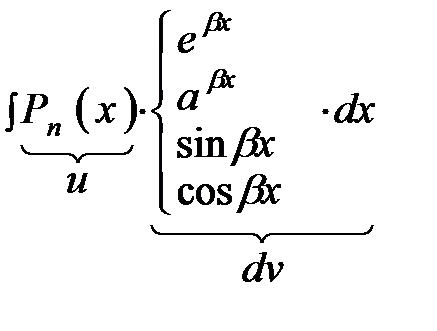
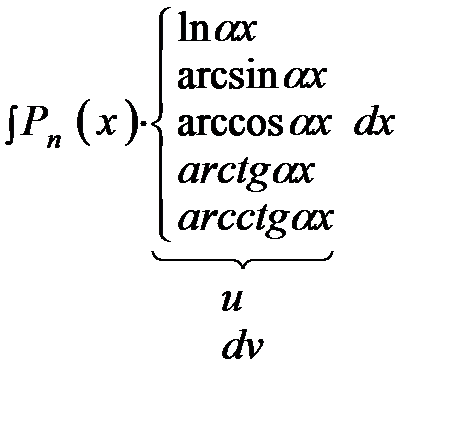
где  - многочлен степени n, α, β – числа.
- многочлен степени n, α, β – числа.
Пример 54. Найти интегралы: а) 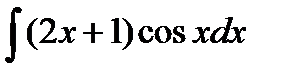 , б)
, б) 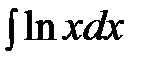 .
.
Решение. Так как под знаком интеграла стоит произведение многочлена 1-й степени на тригонометрическую функцию, то применяя формулу интегрирования по частям (8.1), получаем:
а) 
 .
.
Так как неопределённый интеграл содержит одну произвольную постоянную, то при нахождении функции υ по её известному дифференциалу dυ можно брать одну первообразную (С =0).
б) 
в) Метод замены переменной или метод интегрирования подстановкой заключается во введении новой переменной интегрирования и приведении данного интеграла к новому интегралу, который является табличным или к нему сводящимся.
Пусть требуется вычислить  , причём непосредственно подобрать первообразную для f(x) нельзя, но известно, что она существует. Заменим в подынтегральном выражении переменную х некоторой функцией, имеющей непрерывную производную:
, причём непосредственно подобрать первообразную для f(x) нельзя, но известно, что она существует. Заменим в подынтегральном выражении переменную х некоторой функцией, имеющей непрерывную производную:  . Тогда
. Тогда  и на основании свойства инвариантности формулы интегрирования получаем формулу замены переменной в неопределённом интеграле:
и на основании свойства инвариантности формулы интегрирования получаем формулу замены переменной в неопределённом интеграле:
 . (8.2)
. (8.2)