Определение. Дифференциальное уравнение первого порядка называется
линейным, если искомая функция у и её производная 
входят в это уравнение в первой степени.
(9.9)
Уравнение (9.9) – линейное дифференциальное уравнение первого порядка.
Уравнение (9.9) можно интегрировать различными методами. Рассмотрим метод, основанный на применении подстановки Эйлера-Бернулли 
, с помощью которой линейное уравнение может быть сведено к последовательному интегрированию двух уравнений с разделяющимися переменными.
Подставим 
, 
в (9.9):
.
Сгруппируем слагаемые, содержащие u, и вынесем u за скобку:
(9.10)
Одну из неизвестных функций можно выбрать произвольно. Выберем функцию v так, чтобы скобка обратилась в нуль, т.е. положим
(9.11)
Тогда уравнение (9.10) примет вид:
(9.12)
Из уравнения (9.11) найдём функцию v(x), затем значение v подставим в уравнение (9.12). Решив его, найдём u. Найденные функции u и v подставим в и получим общее решение линейного уравнения.
Пример 72. Найти общее решение линейного уравнения: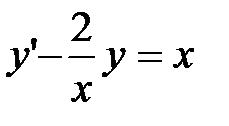 
.
Решение. Ищем общее решение с помощью подстановки Эйлера-Бернулли: .
Тогда, 
.Подставляем найденные значения y и 
в данное уравнение: 
. Группируем слагаемые, содержащие общий множитель 
, который выносим за скобку: 
и полагаем 
(*). Остается: 
(**). Находим из (*):
Подставляем 
(**): 
.
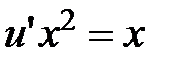Решаем это уравнение:
.
Окончательно получаем: 
- искомое общее решение.
Ответ: 
.
Дифференциальные уравнения II-го порядка
Определение. Дифференциальным уравнением II-го порядка называется уравнение, связывающее независимую переменную, искомую функцию и её первую и вторую производные.
Общий вид дифференциального уравнения II-го порядка:
F (х, у, у', у'') = 0.
Если уравнение разрешено относительно у'', то у'' = f (х, у, у').
|
|
Общее решение дифференциального уравнения II-го порядка содержит 2 произвольные постоянные, а задачу Коши записывают следующим образом:
Рассмотрим один из типов дифференциальных уравнений II-го порядка, допускающих понижение порядка: у'' = f (х), в котором правая часть уравнения зависит только от х.
Уравнения этого типа решают последовательным интегрированием: 
Пример 73. Найти общее решение дифференциального уравнения второго порядка 
.
Решение. Найдём 
, проинтегрировав обе части данного уравнения:
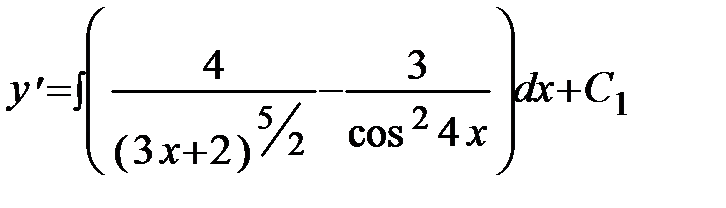. Используя свойства интеграла можно
записать:
.
В первом интеграле имеем сложную степенную функцию, а второй – даёт тангенс того же аргумента: 
, или
.
Для нахождения функции у ещё раз интегрируем обе части полученного уравнения:
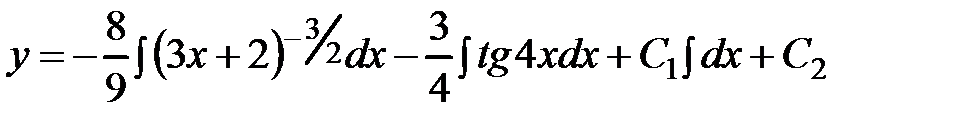
- общее решение.
Линейные дифференциальные уравнения II-го порядка с постоянными коэффициентами
Линейное дифференциальное уравнение II-го порядка с постоянными коэффициентами имеет вид:
, (9.13)
где p, q – числа,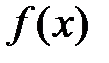 
-некоторая функция.
Уравнение 
(9.14)
называется линейным однородным дифференциальным уравнением II-го порядка (ЛОДУ), соответствующим уравнению (9.13). А уравнение (9.13) в случае 
-линейным неоднородным дифференциальным уравнением (ЛНДУ).