Определение. Степенной ряд вида:
 (10.8)
(10.8)
где функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 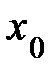 и имеет в этой окрестности производные любых порядков, называется рядом Тейлора функции
и имеет в этой окрестности производные любых порядков, называется рядом Тейлора функции  в окрестности
в окрестности  .
.
Определение. Частный вид ряда Тейлора при 
 (10.9)
(10.9)
называется рядом Маклорена.
Теорема. Пусть  - внутренняя точка интервала сходимости ряда Тейлора
- внутренняя точка интервала сходимости ряда Тейлора
функции  , тогда
, тогда  .
.
Другими словами, в каждой такой точке ряд Тейлора функции  сходится к значению функции.
сходится к значению функции.
Разложение функций в ряд Тейлора можно получить, исходя из известных разложений. При этом можно выполнять следующие действия над степенными рядами внутри их интервала сходимости:
1) два степенных ряда можно почленно складывать и умножать (по правилу умножения многочленов);
2) степенной ряд можно почленно умножить на общий множитель;
3) степенной ряд можно почленно интегрировать и дифференцировать любое число раз.
Приведём ряды Маклорена наиболее часто встречающихся функций:
 (10.10)
(10.10)
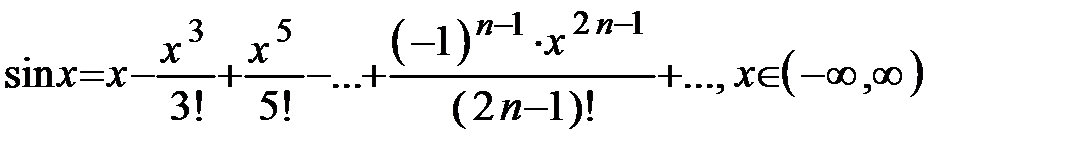 (10.11)
(10.11)
 (10.12)
(10.12)
 (10.13)
(10.13)
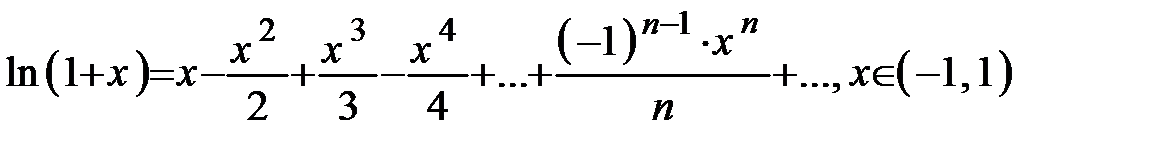 (10.14)
(10.14)
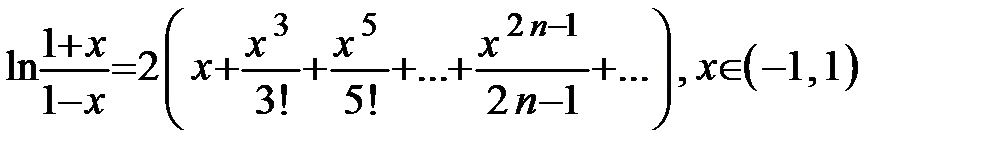 (10.15)
(10.15)
Применение степенных рядов к приближённым вычислениям
Для приближённого вычисления значения функции при помощи ряда следует: 1) по заданному числовому выражению подобрать подходящую функцию; 2) найти подходящую точку, в которой эта функция может быть разложена в ряд Тейлора. При этом интересующее нас значение должно являться значением этого ряда Тейлора в некоторой точке интервала сходимости; 3) пользуясь предыдущими пунктами, получить для интересующего нас числового выражения ряд, при помощи которого найти приближённое значение.
Пример 88. Вычислить  с точностью e = 0,001.
с точностью e = 0,001.
Решение. При вычислении корней воспользуемся биномиальным рядом (10.13). Очевидно, что  , но выбор в качестве х = 33 невозможен, т.к.
, но выбор в качестве х = 33 невозможен, т.к.
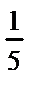 33 Ï (– 1; 1). Преобразуем подкоренное выражение следующим образом:
33 Ï (– 1; 1). Преобразуем подкоренное выражение следующим образом:  . Таким образом, х = 0,0625. Используя биномиальный ряд, получаем:
. Таким образом, х = 0,0625. Используя биномиальный ряд, получаем:

Так как ряд знакочередующийся и  , то по признаку Лейбница
, то по признаку Лейбница  , и для получения требуемой точности достаточно взять первые два члена ряда, следовательно,
, и для получения требуемой точности достаточно взять первые два члена ряда, следовательно, 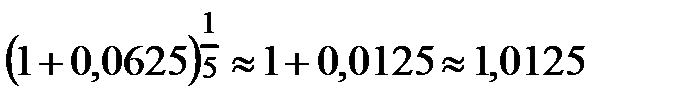 . Тогда
. Тогда  .
.
Пример 89. Вычислить sin70 с точностью e = 0,01.
Решение. Для вычисления значений тригонометрических функций необходимо градусное измерение аргумента перевести в радиальное:
10 » 0,01745 рад, 70 » 0,122 рад, поэтому, используя ряд (10.11), получим:
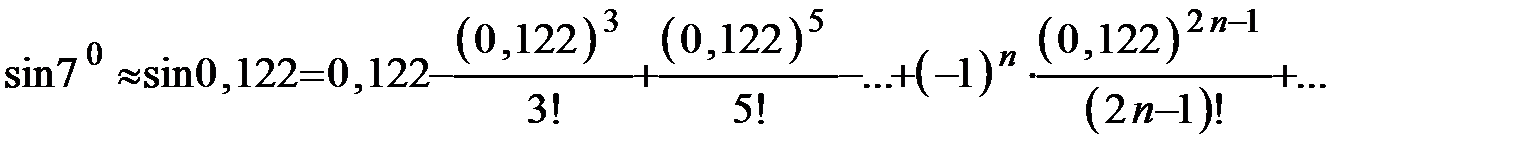

Для достижения нужной точности достаточно взять один член ряда, так как  . Тогда sin70 ≈ 0,122≈0,12.
. Тогда sin70 ≈ 0,122≈0,12.
Пример 90. Вычислить 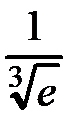 с точностью e = 0,001.
с точностью e = 0,001.
Решение.  . Воспользуемся рядом (10.10) и, положив
. Воспользуемся рядом (10.10) и, положив  , получим:
, получим: 
Так как ряд знакочередующийся, то, ввиду признака Лейбница и того, что  , то достаточно ограничиться первыми четырьмя членами ряда:
, то достаточно ограничиться первыми четырьмя членами ряда: 
 .
.
Пример 91. Вычислить ln1,4 с точностью e = 0,01.
Решение. Для вычисления логарифмов можно воспользоваться рядом (10.14):

Для достижения заданной точности достаточно взять первые три члена ряда, т.к.  . Тогда ln1,4 » 0,4 – 0,08 + 0,021 = 0,341 » 0,34.
. Тогда ln1,4 » 0,4 – 0,08 + 0,021 = 0,341 » 0,34.
Теория вероятностей и математическая статистика
Элементы комбинаторики
При решении ряда теоретических и практических задач требуется из конечного множества элементов по заданным правилам составлять различные комбинации и производить подсчет числа всех возможных таких комбинаций. Такие задачи принято называть комбинаторными.
Комбинаторика широко применяется в теории вероятностей.
Определение. Упорядоченные подмножества данного конечного множества называются размещениями.
Два различных размещения из элементов данного множества отличаются друг от друга либо составом элементов, либо порядком их расположения. Если число элементов множества n, а число элементов подмножества m, то число всех возможных размещений из n элементов по m (0 £ m £ n) обозначают  .
.
 , (11.1)
, (11.1)
где по определению  (n! – эн факториал).
(n! – эн факториал).
Пример 92. В высшей лиге по футболу 18 команд. Борьба идёт за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть
распределены между командами?
Решение. Ясно, что призовые тройки могут отличаться не только составом команд, но и распределением среди этих команд медалей, значит, это будут размещения из 18 команд по 3 (размещения из 18 элементов по 3). Число всех таких размещений: 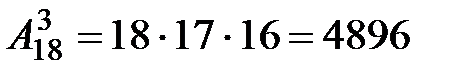
Ответ: 4896 различными способами.
Определение. Перестановкой из n элементов называется размещение из n элементов по n.
Получаемые при этом упорядоченные множества отличаются друг от друга лишь порядком расположения входящих в них элементов. Если множество состоит из n элементов, то число всех возможных перестановок обозначают  :
:  = n! (11.2)
= n! (11.2)
Пример 93. Сколькими способами можно расставить на одной полке 6 различных книг?
Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.  = 6! = 1×2×3×4×5×6 = 720.
= 6! = 1×2×3×4×5×6 = 720.
Ответ: 720 различными способами.
Определение. Произвольные неупорядоченные подмножества данного
множества называются сочетаниями.
Два сочетания будут различными, если они отличаются хотя бы одним элементом (т.е. составом элементов, а порядок расположения элементов не важен). Если n - число элементов множества, а m - число элементов подмножества (m £ n), то число различных сочетаний из n элементов по m элементов обозначают  :
:
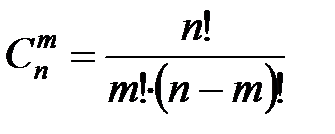 (11.3)
(11.3)
Пример 94. В бригаде из 25 человек нужно выделить четырёх для работы на определённом участке. Сколькими способами это можно Сделайте?
Решение. Так как различные группы из четырёх человек будут отличаться только лишь составом, то их число:
 .
.
Ответ: 12650 способами.