Определение. Случайной величиной Х называется переменная, которая
в результате опыта может принимать с определённой веро-
ятностью то или иное значение, зависящее от исхода опыта.
Случайные величины (СВ) бывают дискретными и непрерывными.
Определение. Случайная величина Х называется дискретной (ДСВ),
если множество её значений конечно либо счётно, т. е.
множество её значений представляет собой конечную последовательность х1, х2, х3,..., хn или бесконечную последовательность х1, х2, х3,..., хn,….
Примером ДСВ могут служить число попаданий в мишень в серии из n выстрелов; число очков, выпавших при одном бросании игральной кости; количество яблок в отдельной упаковке; число покупателей в магазине в данный момент времени и т. д.
Вероятность того, что случайная величина Х примет значение 
, обозначают 
, k= 1, 2, 3,…,n,…
Определение. Соотношение, устанавливающее тем или иным способом связь
между возможными значениями случайной величины и их
вероятностями, называется законом распределения случайной величины.
Простейшей формой этого закона для ДСВ является ряд распределения, который записывается в виде следующей таблицы: Таблица 12
| Х | х1 | х2 | х3 | … | хn | … |
| Р | р1 | р2 | р3 | … | рn | … |
причём, 1) 
, k = 1, 2, 3, …,n,… 2) 
.
| р |
свойствами, является законом распределения
некоторой СВ.
Графической иллюстрацией закона
распределения служит многоугольник
Распределения.
Для этого все возможные значения СВ
откладываются по оси абсцисс, а по оси Рисунок 59
ординат - соответствующие вероятности. Полученные точки 
соединяют отрезками прямых (рисунок 59).
|
|
Пример 104. Из 6 подлежащих аудиторской проверке фирм 4 являются тор-
гово-закупочными. Наудачу отобраны 3 фирмы. Составить закон распределения ДСВ Х - числа торгово-закупочных фирм среди отобранных.
Решение. Возможными значениями Х являются числа: х1=1, х2=2, х3=3. Соответствующие им вероятности равны: 
; 
.
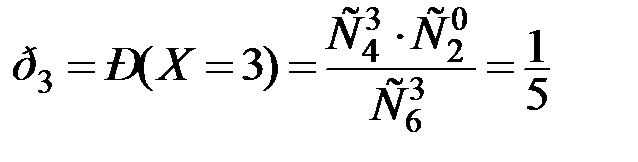Тогда закон распределения рассматриваемой случайной величины Х имеет вид (таблица 13):
Таблица 13
| Х | |||
| Р | 1/5 | 3/5 | 1/5 |
р1+ р2 + р3 = 1
Кроме закона распределения, для характеристики СВ Х часто ис-
пользуют числа, которые описывают СВ суммарно. Такие числа называ-
ют числовыми характеристиками случайной величины.
Для того, чтобы охарактеризовать положение случайной величины на
числовой оси используют математическое ожидание случайной величины
М [Х], т.е. её среднее ожидаемое значение.
Оно равно сумме произведений всех возможных значений на их вероятности:
(при условии абсолютной сходимости ряда).
Оценкой рассеяния значений случайной величины вокруг её математического ожидания служит такая характеристика, как дисперсия.
Определение. Дисперсией Д[Х] дискретной случайной величины Х
называют математическое ожидание квадрата отклонения слу-
чайной величины Х от её математического ожидания:
Д [Х]= М [ Х – М [Х] ] 2. (11.5)
Для вычисления дисперсии часто бывает удобно пользоваться формулой:
Д [Х] = М [Х 2] - (М [Х]) 2. (11.6)
Определение. Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:
|
|
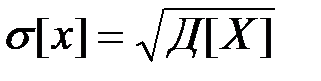. (11.7)
Математическое ожидание определяет центр, относительно которого группируются значения случайной величины, а дисперсия и среднее квадратическое отклонение - как далеко могут отклоняться эти значения от математического ожидания.
Пример 105. Случайная величина Х задана рядом распределения:
Таблица 14
| Х | ||||
| Р | 0,3 | 0,1 | 0,2 | ? |
Найти математическое ожидание М[Х], дисперсию Д[Х], среднее квадратическое отклонение s[Х] и построить многоугольник распределения, вписав в ряд распределения недостающую вероятность.
Решение. 1) Так как 
, то р4 = 1 -(р1+р2+р3)= 1-0,6=0,4. Итак, р4 =0,4.
2) Найдём математическое ожидание М[Х]:
М[Х]= х1р1 + х2р2 + х3р3 + х4р4 = 2 × 0,3 + 4 × 0,1+ 5 × 0,2 + 6 × 0,4 = 4,4
3)Определим дисперсию Д [Х], воспользовавшись формулой (11.6). Для этого напишем закон распределения для случайной величины Х2 (таблица 15):
Таблица 15
| Х2 | ||||
| Р | 0,3 | 0,1 | 0,2 | 0,4 |
и найдём математическое ожидание Х2:
М [Х2] = 4×0,3 + 16×0,1 + 25×0,2 + 36×0,4 = 22,2.
Тогда, искомая дисперсия:
Д [Х] = М [Х2] –(М [Х])2 = 22,2 – (4,4)2 = 2,84,
а среднее квадратическое отклонение: s[Х] = 
3) Построим многоугольник распределения СВ Х, воспользовавшись
таблицей 14(рисунок 60).
Наряду с ДСВ, существуют такие
СВ, у которых множество значений не является счётным, более того, заполняет некоторый сплошной промежуток. С помощью таких СВ можно описывать поведение показателей, связанных с измерением массы, расстояний, концентрации веществ,
Рисунок 60 времени и т. п., например, рост отдельного человека, длина детали; вес отдельного яблока, булки хлеба; время ожидания транспорта на остановке и.т.п.
|
|
Такие СВ можно описать функцией распределения F (х) или плотностью распределения вероятностей f (х).
Определение. Функцией распределения СВ Х F (х) называется вероятность того, что Х примет значения меньшие аргумента х: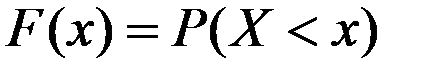 
.
Для дискретной случайной величины Х функция распределения является разрывной, кусочно постоянной функцией.
Определение. Случайная величина Х называется непрерывной (НСВ), если её функция распределения F (x) непрерывна и имеет производную 
, которая, в свою очередь, называется плотностью распределения вероятностей СВ Х.
Плотность распределения вероятности НСВ Х обладает следующими свойствами: 1. 
³ 0; 2. 
;
3. Вероятность 
того, что значение, принятое СВ Х, попадёт в промежуток 
, определяется равенством
(11.8)
Понятия математического ожидания и дисперсии НСВ Х вводятся аналогично случаю ДСВ и вычисляются по формулам:
, (11.9)
и 
, (11.10)
в том смысле, что соответствующие интегралы сходятся.
Определение. СВ Х называется распределённой по нормальному зако-
закону с параметрами 
и s, если её плотность распре-
деления вероятностей имеет вид:
. (11.11)
Вероятностный смысл параметров:
, а 
.
График плотности нормального распре-
деления (нормальная кривая, или
кривая Гаусса) имеет вид, представленный
на рисунке 61. Для расчёта вероятности
попадания нормально распределённой Рисунок 61
СВ Х в промежуток от b до g используется формула 
, (11.12)
где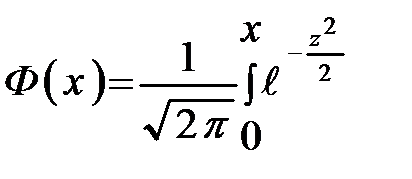 
- функция Лапласа, значения которой находятся по таблице. Свойства 
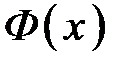: 1) 
; 2) для 
, 
.
Если Х нормально распределена с параметрами 
и s, тогда
- “правило трёх сигм”, т.е. если случайная величина Х распределена по нормальному закону, то её отклонение от математического ожидания практически не превышает ± 3 s.