Будем рассматривать некоторый опыт и систему элементарных событий А, В, С,...., каждое из которых является случайным. Между этими событиями могут существовать некоторые отношения.
Определение. Суммой А+ В событий А и В называется событие, состоя-
щее в наступлении хотя бы одного из событий А или В.
Определение. Произведением А · В событий А и В называется событие,
состоящее в совместном появлении А и В.
Например: Пусть А - попадание в цель при первом выстреле;
В - попадание в цель при втором выстреле.
Тогда событие А + В - хотя бы одно попадание при двух выстрелах, т.е. или первое попадание, второй промах; или первый промах, второе попадание; или два попадания.
Событие А · В - и при первом, и при втором выстрелах попадание в цель.
Определение. Противоположным событию А называется событие 
,
состоящее в не наступлении А.
Теорема 1. (сложения вероятностей несовместных событий)
Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей: А1, А2,..., Аn - несовместны Þ
Р(А1+ А2 +... + Аn ) = Р(А1) + Р(А2) +... + Р(Аn).
Для двух событий: А, В несовместны Þ
Р(А + В) = Р(А) + Р(В).
Следствие 1. Если события А1, А2,... Аn образуют полную группу несовмест-
ных событий, то Р(А1) + Р(А2) +... + Р(Аn) = 1.
Следствие 2. Так как события А и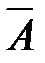 
образуют полную группу несовмест-
ных событий, то Р(А) + Р(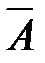) = 1.Отсюда: Р (А)=1- Р ().
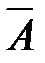Теорема 2. (сложения вероятностей совместных событий)
Вероятность суммы совместных событий А и В равна сумме вероятностейэтих событий без вероятности их совместного появления:
| Рисунок 3 |
Теорема 3. (сложения вероятностей для k совместных событий):
Если события А1, А2, …, Аk – совместны, то вероятность появления хотя бы одного из совместных событий А1, А2, …, Аk равна разности между единицей и вероятностью того, что ни одно из них не наступит:
.
Пример 99. Мишень разделена на три зоны. Вероятность попадания в первую зону равна 0,1, во вторую - 0,3, в третью - 0,4. Найти вероятность попадания в мишень и вероятность промаха при одном выстреле.
Решение. Обозначим события А i - попадание в i -ю зону (i = 1,2,3). Тогда, по условию Р(А1 )=0,1; Р(А2) = 0,3; Р(А3) = 0,4.
Событие А – «попадание в мишень», т.е. либо в первую, либо во вторую, либо в третью зоны, можно представить через А i следующим образом:
А = А1 + А2 + А3. Так как события А i - несовместны, то
Р(А) = Р(А1) + Р(А2) + Р(А3) = 0,1 +0,3 +0,4 = 0,8.
«Промах »- это событие противоположное событию А, следовательно,
.
Ответ: а)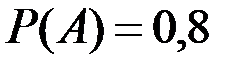 
; б) 
. 
Определение. События А и В называются независимыми, если вероятность наступления одного из них не зависит от того, наступило или нет другое, в противном случае события называются зависимыми.
Теорема 4. (умножения вероятностей независимых событий)
Вероятность произведения независимых событий А и В равна произведению их вероятностей, т.е. 
.
Следствие. Если события А1, А2,... Аn независимы в совокупности, то
Определение. Под условной вероятностью события В по отношению к
событию А (обозначение Р(В / А)) понимается вероятность
осуществления события В, определённая в предположении,
что событие А имело место.
Теорема 5. (умножения вероятностей зависимых событий)
Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, т.е.
Р(А×В) = Р(А) ×Р(В / А).
Следствие. Вероятность произведения n зависимых событий:
Р(А1× А2×...× Аn) = Р(А1)× Р(А2 / А1)×Р(А3/ А1А2)×...×Р(Аn / А1А2...Аn-1).
Пример 100. Многолетними наблюдениями установлено, что в данном районе в сентябре в среднем 10 дней бывают дождливыми. Совхоз должен в течение первых трёх дней сентября выполнить определённую работу.
Определить вероятность того, что ни один из этих дней не будет дождливым.
Решение. Пусть события Аi – «i -го сентября дождя не будет», (i = 1,2,3.) Тогда событие А – «в течение первых трёх дней сентября дождя не будет», можно представить как произведение событий, т.е. А 1× А 2× А 3. Вероятность того, что в какой-то наудачу взятый день сентября (пусть это будет 1-го) дождя не будет, равна: Р (А 1)= 20/30. Вероятность события А 2 – «2-го сентября дождя не будет», можно найти лишь при условии, что известна погода 1-го сентября и т. д. То есть события А 1, А 2, А 3 -зависимые. Найдём условную вероятность Р (А2 / А 1), т.е., что «дождя не будет 2-го при условии, что 1-го сентября его не было»:
Р (А 2/ А 1) =19/29. Далее, Р (А 3/ А 1 А 2) – «вероятность того, что 3 –го сентября дождя не будет, если его не было 1-го и 2-го», равна: Р (А 3/ А 1 А 2)=18/28. Итак,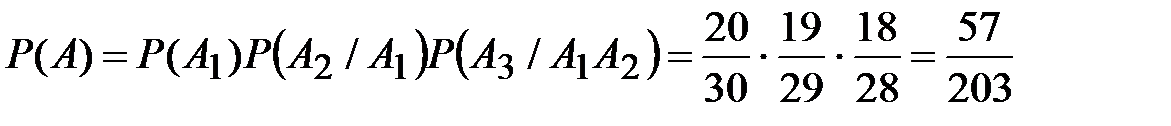 
.
Ответ: 
.
Пример 101. В первой группе 18 студентов, из них 3 отличника.Во второй группе- 20 студентов, из них 5 отличников. Наугад выбирают по одному студенту из каждой группы. Какова вероятность, что оба студента отличники?
Решение. Рассмотрим следующие элементарные события:
А – «студент, выбранный из первой группы - отличник»,
В – «студент, выбранный из второй группы -отличник»,
Тогда, событие – «оба студента отличники» - можно представить как произведение А × В, т. е. «и А, и В ». При этом А и В - независимые события и
Р (А)=3/18 = 1/6, Р (В) = 5/20= 1/4.
Тогда, Р (АВ)= Р (А)× Р (В) = (1/6) ×(1/4) = 1/24.
Ответ: Р (АВ) = 1/24.
Пример 102. В условиях предыдущей задачи определить вероятность того, что один из выбранных студентов отличник, а другой – не является отличником.
Решение. Рассмотрим следующие элементарные события:
А 1-студент, выбранный из первой группы - отличник, Р (А 1)=1/6;
А 2-студент, выбранный из второй группы -отличник, Р (А 2)=1/4;
В 1 -студент, выбранный из первой группы не является отличником, Р (В 1) =5/6; В 2-студент,выбранный из второй группы не является отличником, Р (В 2)=3/4.
Тогда вероятность того, что студент, выбранный из первой группы отличник,, а из второй группы - не отличник:
Р(А1В2)=Р(А1) × Р(В2)= (1/6)× (3/4)=1/8. Определим теперь вероятность того, что студент из первой группы не отличник, из второй - отличник: Р(А2В1)= Р(А2) × Р(В1)= (1/4) (5/6)=5/24. Чтобы определить вероятность того, что студент, выбранный из группы (безразлично какой), окажется отличником, а из другой группы не отличником, применим теорему сложения для несовместных событий А1В2 и А2В1: Р= Р(А1В2)+Р(А2В1)= 1/8+5/24 =1/3.
Ответ: Р = 1/3.
Пример 103. В городе 2 коммерческих банка, оценка надёжности которых –
0,95 и 0,85 соответственно. В связи с определением хозяйственных перспектив развития города администрацию интересуют ответы на следующие вопросы:
а) какова вероятность того, что в течение года обанкротится только один банк; б) что обанкротится хотя бы один банк?
Решение. Обозначим событие А1 - «обанкротился первый банк»;
А2 - «обанкротился второй банк». Тогда 
, 
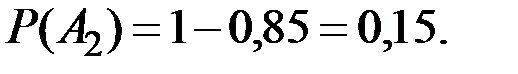а) Событие А - «обанкротится только один банк» означает, что либо обанкротится первый банк и второй останется надёжным, либо обанкротится второй банк и первый останется надёжным. То есть
. Учитывая, что события 
и 
несовместны, а события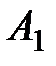 
и 
и 
и 
- независимы, имеем: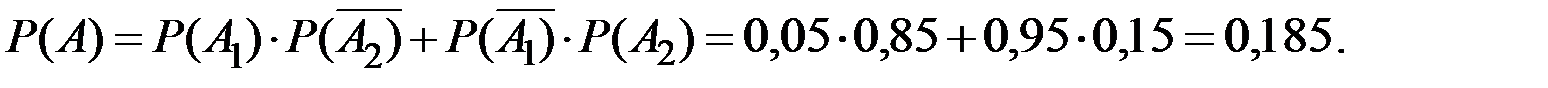 
б) Событие В – «обанкротится хотя бы один банк » означает, что либо обанкротится первый банк и второй останется надёжным, либо обанкротится второй банк и первый останется надёжным, либо они оба обанкротятся. Такую задачу более рационально решать через противоположное событие. Событие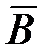 
- «ни один из банков не обанкротится » (и первый, и второй останутся надёжными). Тогда 
. Окончательно 
Ответ: а) 
, б)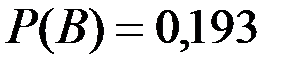 
.