Определение. Генеральной совокупностью (Г.С.) называется вся совокупность значений, принимаемых изучаемым признаком Х.
Определение. Выборкой объёма n из генеральной совокупности называется
набор значений х1, х2, х3, …, хn, являющихся результатами
наблюдений (измерений) признака Х.
Как правило, объём выборки велик, поэтому предварительно проводят, так называемую первичную обработку результатов измерений. Целью такой обработки является уменьшение числа наблюдений, но так, чтобы закономерности, присущие признаку, были сохранены.
В зависимости от вида Г.С. различают два вида первичной обработки опытных данных.
Если Г.С. изучаемого признака Х представляет собой дискретное множество, применяется метод ранжирования, который предполагает расположение в порядке возрастания значений наблюдаемого признака с указанием количества повторов каждого значения.
Пример 106. Пусть Х – количество сбоев станка в течение смены. В результате проведения наблюдений получены следующие данные: 5, 1, 3, 2, 4, 1, 2, 3, 4, 5, 3, 2, 2, 1, 2, 5, 4, 4, 4, 3, 1, 2, 3, 4, 5. Провести ранжирование.
Решение. Расположим результаты измерений следующим образом:
1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5.
4р. 6р. 5р. 6р. 4р.
Запишем полученные результаты в виде таблицы 16:
Таблица 16
| Хi | |||||
| ni |
Значения изучаемого признака, расположенные в верхней строке таблицы, т.е. 1, 2, 3, 4, 5 называют вариантами, а соответствующие им значения 4, 6, 5, 6, 4 называют частотами ( ni). Ряд, представленный таблицей 16, называют вариационным (статистическим) рядом частот.
Отметим, что сумма частот всегда совпадает с объёмом выборки, т.е.
 .
.
В нашем случае  и
и  .
.
Иногда используют вариационный (статистический) ряд относительных частот, где частоты  заменяют на относительные частоты
заменяют на относительные частоты  .
.
В рассматриваемом примере 106 вариационный ряд относительных частот имеет вид (таблица 17):
Таблица 17

| |||||

| 0,16 | 0,24 | 0,20 | 0,24 | 0,16 |
Ясно, что сумма относительных частот равна 1, т.к.

В рассматриваемом примере: 
Рассмотрим случай, когда генеральная совокупность наблюдаемого признака не является дискретным множеством. В этом случае все данные (выборку объёма n) необходимо разбить на “ k ” интервалов одинаковой длины. Число интервалов определяют по эмпирической формуле Стэрджесса:
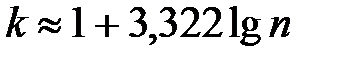 , (11.13)
, (11.13)
округляя до целого числа. Длину интервала  определяют так:
определяют так:
 , (11.14)
, (11.14)
где  - наибольшая, а
- наибольшая, а 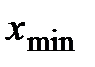 - наименьшая варианты выборки.
- наименьшая варианты выборки.
Группируя отдельные наблюдения в интервалы и располагая их в возрастающем порядке, получим так называемый интервальный ряд распределения (таблица 18):
Таблица 18
| х | [  ; ;  + +  ) )
| [  + +  ; ;  +2 +2  ) )
| [  +(к-1) +(к-1)  ; ;  +к +к  ] ]
| |

| 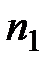
| 
| … | 
|
где 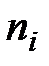 - число значений, попавших в i - тый интервал.
- число значений, попавших в i - тый интервал.
От интервального ряда (таблица 18) можно перейти к cсоответствующему вариационному ряду частот или вариационному ряду относительных частот, взяв вместо интервалов по одному представителю из этих интервалов. Как правило, в качестве представителей берут середины интервалов:
 (11.15)
(11.15)
Полигон и гистограмма
Для наглядного представления статистических распределений пользуются графическим изображением вариационных рядов. Мы будем использовать два вида графиков: полигон и гистограмму.
При построении полигона частот для дискретного ряда распределения (таблица 16) или полигона относительных частот для ряда (таблица 17) по оси абсцисс откладывают значения вариант, а по оси ординат - соответствующие им частоты или относительные частоты.
Полученные точки соединяют отрезками прямых.
 В качестве примера построим полигон
В качестве примера построим полигон
относительных частот для ряда,
представленного таблицей 17 примера 106
(рисунок 62):
При построении гистограммы
относительных частот для интервального
ряда распределения (таблица 18) по оси абсцисс Рисунок 62
откладывают интервалы значений признака. На каждом интервале как на основании строится прямоугольник с высотой
 (11.16)
(11.16)
(плотность относительной частоты), площадь которого в определённых единицах масштаба равна относительной частоте  вариант, попавших в i –ый интервал. Следовательно, площадь гистограммы относительных частот равна
вариант, попавших в i –ый интервал. Следовательно, площадь гистограммы относительных частот равна  .
.
Пример 107. Для данного интервального ряда построить гистограмму относительных частот (таблица 19):
Таблица 19
| X | [2,2; 2,4) | [2,4; 26) | [2,6; 2,8) | [2,8; 3,0) | [3,0; 3,2) | [3,2; 3,4] |
| ni |
 Решение. Объём данной выборки: n = 4 + 6 + 5 + 2 + 6 + 2 = 25.
Решение. Объём данной выборки: n = 4 + 6 + 5 + 2 + 6 + 2 = 25.
Ширина интервалов:  = 0,2.
= 0,2.
Для построения гистограммы вычислим
для каждого интервала по форму-
ле (11.16) плотность относительной
частоты  . Полученные результаты
. Полученные результаты
занесём в таблицу 20 и построим
гистограмму относительных
частот (рисунок 63):
Таблица 20 Рисунок 63
| Х | [2,2; 2,4) | [2,4; 26) | [2,6; 2,8) | [2,8; 3,0) | [3,0; 3,2) | [3,2; 3,4] |
| h i | 0,8 | 1,2 | 0,4 | 1,2 | 0,4 |