Одним из основных понятий в теории вероятностей является событие.
Определение. Под случайным событием будем понимать всякое явление, которое может произойти или не произойти в результате испытания (опыта).
Например: испытание -бросание монеты, случайное событие - выпадение герба.
Определение. Говорят, что несколько событий образуют в данном испытании полную группу, если в результате испытания должно произойти хотя бы одно из них.
Например: испытание - бросание двух монет. События А1 -выпадение двух гербов и А2 -выпадение двух цифр до полной группы дополняют события А3 -выпадение герба на первой и цифры на второй монетах и А4 -выпадение цифры на первой и герба на второй монетах.
Определение. События называются равновозможными, если нет никаких
оснований предполагать, что одно из них более возможно, чем
другие.
Определение. События называются несовместными в данном испытании,
если появление одного из них исключает появление всех ос-
тальных.
Определение. События, которые удовлетворяют трём условиям:
1) образуют полную группу; 2)несовместны; 3) равновозможны называются элементарными событиями, или исходами.
Определение. Исход опыта называется благоприятствующим событию А,
если осуществление этого исхода влечёт за собой осуществле-
ние события А.
Например, при одном броске игральной кости может произойти одно из шести событий Аk – «выпадение k очков » (k =1,2,3,4,5,6).
В силу симметрии кости можем считать все события Аk равновозможными, далее, они несовместны (появление одного из них исключает появление других при одном броске кости), и они образуют полную группу. Следовательно, события Аk - исходы данного опыта. Для события А – «появление не более двух очков» - благоприятствующими исходами являются только два: А1 -выпадение одного очка и А2 - выпадение двух очков.
|
|
Классическое определение вероятности
Определение. Вероятностью Р(А) наступления события А называется
отношение m – числа благоприятствующих событию
А исходов к n – числу 
всех возможных исходов опыта:
(11.4)
Из определения вероятности следует, что 0£ Р(А)£ 1. Так, достоверному событию (т.е. событию, которое должно произойти при каждом исходе) соответствует вероятность Р(А)=1, а невозможному событию (т.е. событию, которое заведомо не произойдёт) соответствует вероятность Р (А)= 0.
Пример 96. В урне находятся 3 белых и 4 чёрных шара. Из урны наугад вынимается один шар. Найти вероятности следующих событий:
а) извлеченный шар - синий; б) извлеченный шар - белый.
Решение. Опыт - извлечение из урны одного шара. Число исходов такого опыта: n=7.
а) Обозначим А - событие, состоящее в появлении синего шара. Число исходов благоприятствующих А: m=0, так как синих шаров в урне нет (А - невозможное событие). Следовательно, Р(А) = 0.
б) Обозначим В - событие, состоящее в появлении белого шара.
Число исходов благоприятствующих В: m=3. Значит, 
.
Ответ: а) 0; б) 
.
Пример 97. На каждой из 7 одинаковых карточек напечатана одна из следующих букв: н, о, п, р, с, т, у. Найти вероятность того, что на пяти взятых наугад и расположенных в ряд карточках можно будет прочесть слово «спорт».
Решение. Общее число возможных исходов равно числу размещений из 7
по 5 (важен порядок расположения карточек), т.е.
, а благоприятствует событию А–« набрано слово «спорт» » - лишь один исход, т.е. m = 1. Поэтому 
.
|
|
Ответ: 
.
Пример 98. На 9 вакантных мест по определённой специальности претендуют 15 безработных, состоящих на учёте в службе занятости и 10 работающих, но желающих поменять специальность. Какова вероятность того, что 6 безработных получат работу?
Решение. Опыт состоит в том, что из 25 претендентов нужно выбрать 9 на вакантные места. Общее число исходов опыта равно числу сочетаний из 25 по 9, т.е. 
. Подсчитаем число исходов опыта, благоприятствующих событию В - «6 из 9 вакансийполучат безработные», т.е. 6 безработных и 3 работающих займут вакантные места.
Такую девятку можно составить двумя последовательными выборами: 1) 6 безработных можно выбрать столькими способами, сколько сочетаний можно составить из 15 по 6, т.е. 
; 2) вариантов выбора троих работающих на оставшиеся места может быть столько, сколько сочетаний можно составить из 10 по 3, т.е.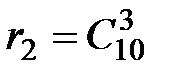 
. Тогда выбор «6 безработных и 3 работающих » можно осуществить 
– способами. Итак, число исходов благоприятных событию В: 
. Отсюда, по классическому определению вероятности имеем: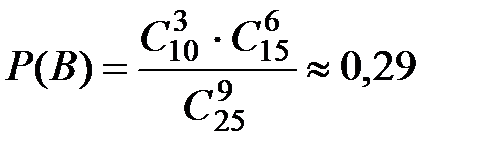 
.
Ответ: 
.