Основные статистические показатели

Если из генеральной совокупности признака Х извлечена выборка

х₁, х₂, х₃, …, х_n объёма n, то поведение признака Х в пределах этой выборки описывается следующими выборочными статистическими характеристиками:

- выборочное среднее (или среднее арифметическое “взвешенное”):

(11.17)

- “исправленная” выборочная дисперсия:

(11.18)

- среднее квадратическое отклонение: 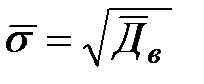(11.17)

Выборочная дисперсия и среднее квадратическое отклонение слу-

жат основными мерами вариации, рассеяния изучаемого признака вокруг

его среднего значения.

- коэффициент вариации: (11.20)

Коэффициент вариации является относительным показателем изменчивости признака Х и выражается в процентах. Изменчивость принято считать незначительной, если ; средней, если и значительной, если .

Для определения показателей меры косости и меры крутости кривой действительного распределения вычисляют коэффициент асимметрии А и

эксцесс Е: (11.21)

(11.22)

Если кривая распределения симметрична относительно средней, то А = 0

(нормальное распределение), если же А>0 – скос кривой вправо, при А <0 скос влево (рисунок 64).

Рисунок 64

Для нормального закона распределения эксцесс Е=0; кривые, более

островершинные по сравнению с нормальной, обладают положительным эксцессом (Е > 0); для кривых, более плосковершинных, Е<0 (рису-

нок 65).

Рисунок 65

совокупности. Критерий согласия Пирсона

При изучении генеральной совокупности часто необходимо знать закон распределения изучаемого признака Х.

Пусть вид гистограммы, а также значения А и Е позволяют выдвинуть гипо-

тезу о нормальном распределении исследуемого признака с плотностью:

,

где 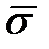- оценка среднего квадратического отклонения,

- оценка математического ожидания.

Проверка гипотезы о предполагаемом законе неизвестного распределения проводится при помощи так называемых критериев согласия. Рассмотрим один из них – критерий c² К. Пирсона.

Для этого будем сравнивать эмпирические (наблюдаемые) частоты n_i и теоретические (вычисленные в предположении нормальности распределения) частоты при помощи статистики:

(11.23)

Величина является случайной и имеет распределение c² с

S = k – r – 1 числом степеней свободы. Здесь k – число интервалов выбор-

ки, а r – число параметров теоретического закона распределения. Так как

нормальное распределение определяется двумя параметрами -

математическим ожиданием и средним квадратическим отклонением,

которые оценивались по выборке, то r = 2 и тогда S = k – 3.

При статистической проверке гипотез задают уровень значимости

, который представляет собой вероятность допустить ошибку первого рода, т.е. отвергнуть правильную гипотезу. Обычно уровень значимости принимают равным 0,05 или 0,01.

Значение 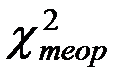может быть найдено по заданному уровню значи- мости и числу степеней свободы k при помощи стандартных таблиц

(приложение 5). Гипотеза не отвергается, если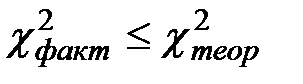

и отвергается, если .