Интервальное оценивание параметров генеральной совокупности

 

Статистические показатели выборочной совокупности являются приближёнными оценками неизвестных параметров генеральной совокупности. Оценка может быть представлена одним числом (точечная оценка) или некоторым интервалом (интервальная оценка), в котором с определённой вероятностью может находиться оцениваемый параметр. Так, выборочная средняя является точечной оценкой генеральной средней , а “исправленная” выборочная дисперсия - точечной оценкой генеральной дисперсии .

Интервальной называют оценку, которая характеризуется двумя

числами – концами интервала, покрывающего оцениваемый параметр.

 

Определение. Доверительным называют такой интервал, который с

заданной вероятностью (надёжностью ) покрывает оце-

ниваемый параметр.

Центр такого интервала – выборочная оценка, а концы интервала (или доверительные границы) определяются средней ошибкой оценки и уровнем доверительной вероятности.

Так, доверительный интервал для генеральной средней определяется по формуле:

, (11.24)

где -значение аргумента функции Лапласа 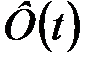, при котором ,

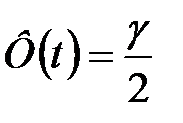находят по таблице приложения 3 при заданной надёжности или доверительной вероятности и известном объёме выборки .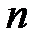

Для нахождения доверительного интервала для среднего квадратичес-кого отклонения в генеральной совокупности по найденному выбороч-

ному значению используют формулу:

, (11.25)

где, 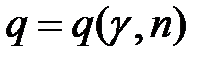- находится по таблице приложения 4 при заданной надёжности или доверительной вероятности и известном объёме выборки .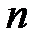

 

Пример 108. Рассмотрим в качестве изучаемого признака X уровень минерализации дренажного стока в г/л, измеренный в течении 50 дней:

5,8 6,4 8,6 8,0 7,0 6,7 6,5 5,7 7,4 7,0

6,5 7,8 7,4 6,5 7,8 9,1 5,7 7,4 5,7 7,0

8,2 8,0 8,4 7,3 5,4 5,1 7,8 7,6 6,4 5,4

7,3 6,5 7,7 6,5 8,5 7,3 7,6 7,3 7,2 9,2

6,9 5,4 6,8 6,7 5,8 6,2 6,7 7,2 7,1 8,4.

1. Выполнить сводку данных наблюдения.

2. Построить интервальный ряд распределения и статистическое

распределение выборки.

3. Построить полигон и гистограмму относительных частот и по их виду выдвинуть гипотезу о законе распределения исследуемой статистической величины.

4. Вычислить основные статистические показатели (выборочную среднюю

выборочную дисперсию, среднее квадратическое отклонение, коэффициент вариации а также показатели мер косости и крутости.

5. Проверить по критерию согласия Пирсона выдвинутую гипотезу о законе распределения. Построить график теоретической плотности распределения.

6. Найти доверительные интервалы для среднего значения и среднего квадратического отклонения в генеральной совокупности на 5% уровне значимости.

7. Провести анализ результатов и Сделайте выводы.

Решение. 1. Выборочная совокупность содержит результаты 50 наблюдений, значит объём выборки = 50. Определим число интервалов:

.

Просматривая всю выборку, определим наибольшую и наименьшую варианты: = 9,2 (г/л) и 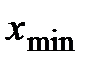= 5,1 (г/л); тогда длина интервалов

(г/л).

Границы интервалов вычисляем по формуле: , (i=0,1,2, …, k -1)

где .

Проведём сводку данных наблюдения с помощью рабочей таблицы 21, состоящей из трёх столбцов. В первый столбец заносят полученные интервалы, причём значение, совпадающее с правой границей интервала, относят к тому интервалу, для которого оно является левой границей.

Просматривая выборку, отмечаем каждое значение путём проставления чёрточки против соответствующего интервала во втором столбце таблицы.

В третий столбец записывается сумма чёрточек каждой строки, т.е. число значений выборки попавших в каждый интервал: частота .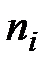

Таблица 21

Интервалы	Сводка	Частота
[5,1; 5,7)	////
[5,7; 6,3)	///// /
[6,3; 6.9)	///// ///// /
[6,9; 7,5)	///// ///// ////
[7,5; 8,1)	///// ///
[8,1; 8,7)	/////
[8,7; 9,3]	//

2. Интервальный ряд распределения перепишем в виде таблицы 22.

Таблица 22

Интервалы	[5,1-5,7)	[5,7-6,3)	[6,3-6,9)	[6,9-7,5)	[7,5-8,1)	[8,1-8,7)	[8,7-9,3]

Статистический ряд распределения частот мы получим, если вместо интервалов возьмём по одному представителю, а именно, середины интервалов, т.е. 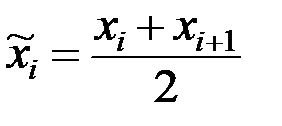(таблица 23).

Таблица 23

(г/л)	5,4		6,6	7,2	7,8	8,4	9,0

Ряд, представленный таблицей 24, где каждому 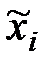поставлена в соответствие относительная частота , будет статистическим рядом распределения относительных частот.

Таблица 24

(г/л)	5,4		6,6	7,2	7,8	8,4	9,0
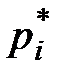
	0,08	0,12	0,22	0,28	0,16	0,10	0,04

.

3. Для построения гистограммы относительных частот необходимо (как уже отмечалось ранее) знать длины интервалов 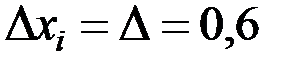и высоты

прямоугольников (плотность относительной частоты, таблица 25).

Таблица 25

Интервалы	5,1-5,7	5,7-6,3	6,3-6,9	6,9-7,5	7,5-8,1	8,1-8,7	8,7-9,3
	0,133	0,200	0,367	0,467	0,267	0,167	0,067

Строим гистограмму относительных частот. Соединяя середины верх-

них сторон прямоугольников отрезками прямых линий, получим полигон

относительных частот (штриховая линия) (рисунок 66).

 

Рисунок 66

По виду гистограммы (полигона) выдвигаем гипотезу о нормальном распределении изучаемого признака Х.

4. Вычислим основные статистические показатели. Для удобства вычислений воспользуемся таблицей 26. При этом нужно учитывать следующие указания о точности вычислений: среднее выборочное вычисляется на один порядок точнее, чем производилось наблюдение, а выборочную дисперсию и среднее квадратическое отклонение – на один порядок точнее среднего значения.

Таблица 26

№
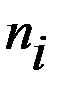
	5,4		21,60	-1,67	11,1556	-18,62985	31,111853
				-1,07	6,8694	-7,35023	7,864776
	6,6		72,60	-0,47	2,4299	-1,14205	0,536765
	7,2		100,80	0,13	0,2366	0,03076	0,003999
	7,8		62,40	0,73	4,2632	3,11214	2,271859
	8,4			1,33	8,8445	11,76319	15,645036
	9,0			1,93	7,4498	14,37811	27,749760
å			353,40		41,2490	2,16207	85,184048

Чтобы заполнить столбец № 4 нужно перемножить соответствующие элементы 2–го и 3–го столбцов.

Найдя сумму элементов 4–го столбца и применив формулу (11.15), вычислим среднее выборочное:

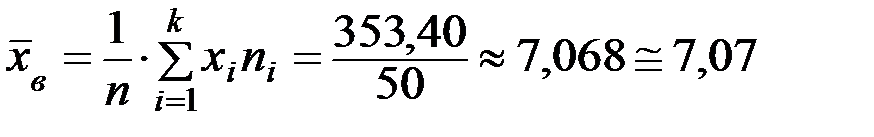(г/л).

Элементы столбца № 5, , найдём, если от каждого элемента 2–го столбца вычтем найденное . Далее, возводя полученные разности в квадрат и умножая на соответствующие элементы 3–го столбца (), получаем элементы 6–го столбца. Перемножая соответствующие элементы 5–го и 6–го столбцов, заполняем 7–ой и аналогично 8–ой столбцы

Сумму элементов столбца № 6 используем для вычисления по формуле (11.14) “исправленной” выборочной дисперсии:

,

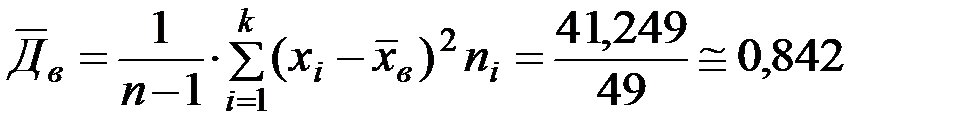а среднее –квадратическое отклонение: 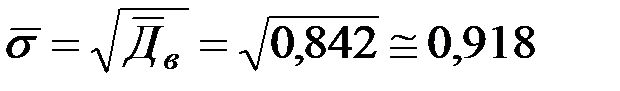(г/л).

Коэффициент вариации:

,

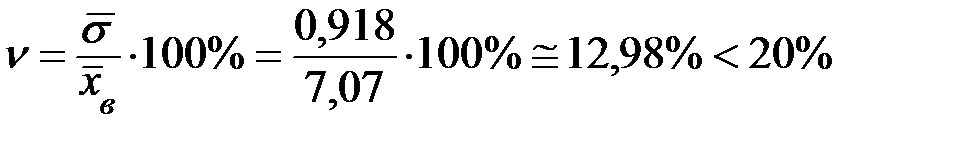Следовательно, изменчивость минерализации можно считать средней.

Суммы элементов столбцов № 7 и № 8 используем для вычисления по формулам (11.21) и (11.22) показателей мер косости и крутости.

 

Асимметрия:

Так как А > 0, то это указывает на правый скос кривой распределения относительно нормальной кривой.

Эксцесс:

и так как Е < 0, то линия распределения вариант данного ряда проходит

ниже кривой нормального распределения. Так как показатели А и Е по абсолютной величине достаточно мало отличаются от нуля, то это подтверждает наше предположение о нормальном распределении минерализации дренажного стока.

5. При заданном уровне значимости 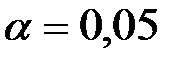проверим по критерию Пирсона эту гипотезу. Для этого найдём теоретические частоты и сравним их с эмпирическими частотами как было указано ранее.

Теоретические частоты нормально распределённого признака вычислим по формуле: 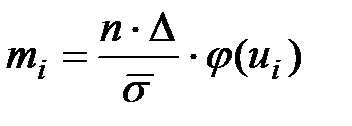, (11.26)

где (11.27), а

Значения функции находятся по таблице (приложение 2).

В нашем примере объём выборки n = 50, длина интервалов

=0,6, =7,07; 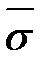=0,918. Тогда, используя формулу (11.26), имеем:

,

где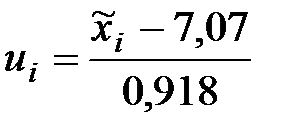

Все необходимые вычисления сведём в таблицу 27:

Таблица 27

№						-
	-1,67	-1,82	0,0761	2,49		1,51	0,916
	-1,07	-1,17	0,2012	6,58		-0,58	0,051
	-0,47	-0,51	0,3503	11,45		-0,45	0,018
	0,13	0,14	0,3951	12,92		1,08	0,090
	0,73	0,80	0,2897	9,47		-1,47	0,228
	1,33	1,45	0,1394	4,56		0,44	0,042
	1,93	2,10	0,0440	1,44		0,56	0,218
∑							1,563

Мы получили

По таблице критических точек распределения (приложение 5) с заданным уровнем значимости 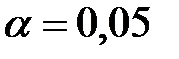и числом степеней свободы

S = k – 3 = 7 – 3 = 4 находим

Так как , то нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности. Таким образом, мы можем построить теоретическую кривую распределения с плотностью распределения .

Построим график этой функции для точек, абсциссами которых служат -середины выбранных интервалов (i =1, 2, …, 7). Вычисление 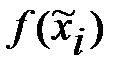можно упростить: .

Значения и 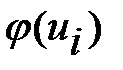можно взять из таблицы 28. Итак, имеем

Таблица 28

№
	5,4	-1,82	0,0761	0,083
		-1,17	0,2012	0,219
	6,6	-0,51	0,3503	0,382
	7,2	0,14	0,3951	0,430
	7,8	0,80	0,2897	0,312
	8,4	1,45	0,1394	0,152
	9,0	2,10	0,0440	0,048

Кроме точек, полученных в таблице 28, построим точку, соответствующую

максимуму плотности распределения или (7,07; 0,434)

и точки перегиба: или (7,07 ± 0,918; 0,263),

т.е. точки: (7,988 0,263) и (6,152; 0,263).

Строим теоретическую кривую распределения (на рисунке 66 это сплош-

ная линия).

6. Вычислим доверительный интервал для средней в генеральной совокуп-

ности по формуле (11.24). Для этого по таблице приложения 3 находим , где 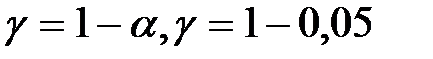, γ = 0,95; n = 50.

Подставляя в формулу эти данные, а также 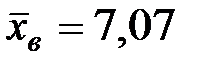и 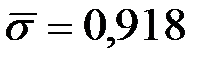имеем: 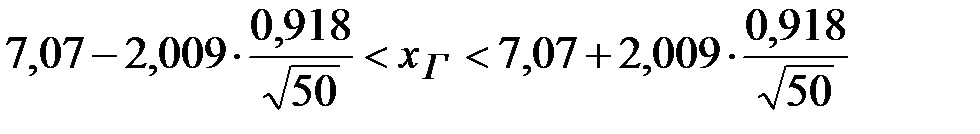или (г/л).

Таким образом, минимальная доверительная граница, или гарантированный минимум среднего значения минерализации в генеральной совокупности равен 6,8 (г/л), а возможный максимум – 7,3 (г/л).

Аналогично определим доверительный интервал для среднего квадратического отклонения, используя формулу (11.25). Зададим доверительную вероятность 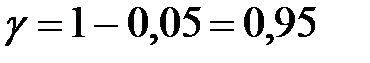и по таблице приложения 4 найдём

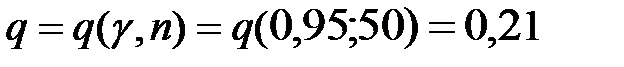. Тогда,

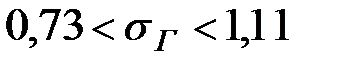или (г/л)

Итак, с вероятностью 0,95 мы можем утверждать, что среднее квадратическое отклонение для генеральной совокупности находится в интервале (0,73; 1,11).

7. Проведём анализ полученных результатов. Запишем кратко полученные результаты: ; ; , ;

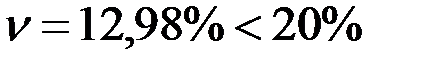; А = 0,056 >0; Е = - 0,601 < 0.

На основании этих результатов можно Сделайте следующие выводы:

- Выборочная средняя измерений уровня минерализации дренажного стока равна 7,07 г/л, а генеральная средняя изучаемого признака находится в интервале от 6,8 г/л до 7,3 г/л.

Изменчивость измерений уровня минерализации дренажного стока характеризуется средним квадратическим отклонением, которое для выборочной совокупности составляет 0,918 (г/л), при этом, коэффициент вариации равен 12,98%, что говорит о средней изменчивости измерений.

- В генеральной совокупности среднее квадратическое отклонение

находится в интервале от 0,73 г/л до 1,11 г/л.

- На основании проверки критерия согласия Пирсона мы можем утверждать, что уровень минерализации дренажного стока подчиняется нормальному закону распределения с плотностью

.