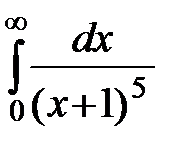В задачах 10.1-10.2 даны координаты точек А, В, С и М. Требуется: 1) составить канонические уравнения прямой АВ; 2) составить уравнение плоскости Q1, проходящей через точку С перпендикулярно прямой АВ; 3) составить уравнение плоскости Q2, проходящей через точки А, В и С; 4) составить канонические уравнения прямой, проходящей через точку М перпедикулярно плоскости Q1.
10.1 А(3; -1; 5), В(7; 1; 1), С(4; -2; 1), М(-1; 4; 2)
10.2 А(-1; 2; 3), В(3; 4; -1), С(0; 1; -1), М(2; -3; 4)
10.3 А(2; -3; 7), В(6; -1; 3), С(3; -4; 3), М(-1; 3; -2)
10.4 А(0; -2; 6), В(4; 0; 2), С(1; -3; 2), М(2; -3; 1)
10.5 А(-3; 1; 2), В(1; 3; -2), С(-2; 0; -2), М(3; -1; 2)
10.6 А(-2; 3; 1), В(2; 5; -3), С(-1; 2; -3), М(2; 3; -1)
10.7 А(-4; 0; 8), В(0; 2; 4), С(-3; -1; 4), М(3; -2; 6)
10.8 А(1; 4; 0), В(5; 6; -4), С(2; 3; -4), М(7; 2; -1)
10.9 А(4; -4; 9), В(8; -2; 5), С(5; -5; 5), М(5; -7; 3)
10.10 А(5; 5; 4), В(9; 7; 0), С(6; 4; 0), М(6; -4; 7)
10.11 А(-3; -2; -4), В(-4; 2; -7), С(5; 0; 3), М(-1; 3; 0)
10.12 А(2; -2; 1), В(-3; 0; -5), С(0; -2; -1), М(-3; 4; 2)
10.13 А(5; 4; 1), В(-1; -2; -2), С(3; -2; 2), М(-5; 5; 4)
10.14 А(3; 6; -2), В(0; 2; -3), С(1; -2; 0), М(-7; 6; 6)
10.15 А(1; -4; 1), В(4; 4; 0), С(-1; 2; -4), М(-9; 7; 8)
10.16 А(4; 6; -1), В(7; 2; 4), С(-2; 0; -4), М(3; 1; -4)
10.17 А(0; 6; -5), В(8; 2; 5), С(2; 6; -3), М(5; 0; -6)
10.18 А(-2; 4; -6), В(0; -6; 1), С(4; 2; 1), М(7; -1; -8)
10.19 А(-4; -2; -5), В(1; 8; -5), С(0; 4; -4), М(9; -2; -10)
10.20 А(3; 4; -1), В(2; -4; 2), С(5; 6; 0), М(11; -3; -12)
Введение в математический анализ
В задачах 11.1 – 11.20 найдите указанные пределы.
| 2 х |
| 3 х –1 |
| + |
| + |
| + |
| 3 х –1 |
| 2 х –4 |
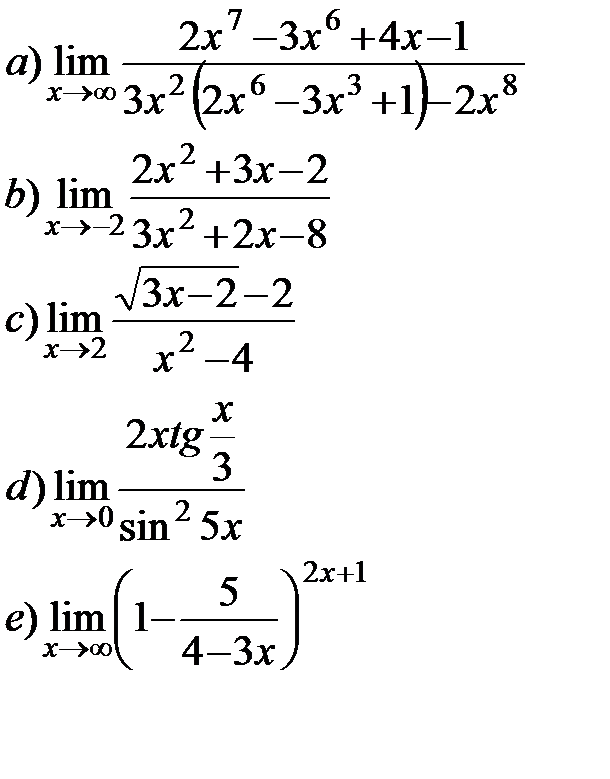 11.2.
11.2. 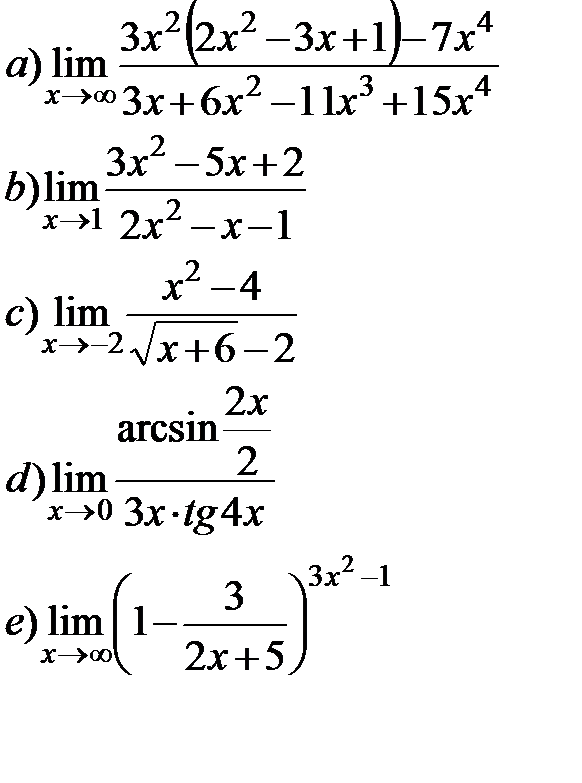
11.3.  11.4.
11.4. 
11.5.  11.6.
11.6. 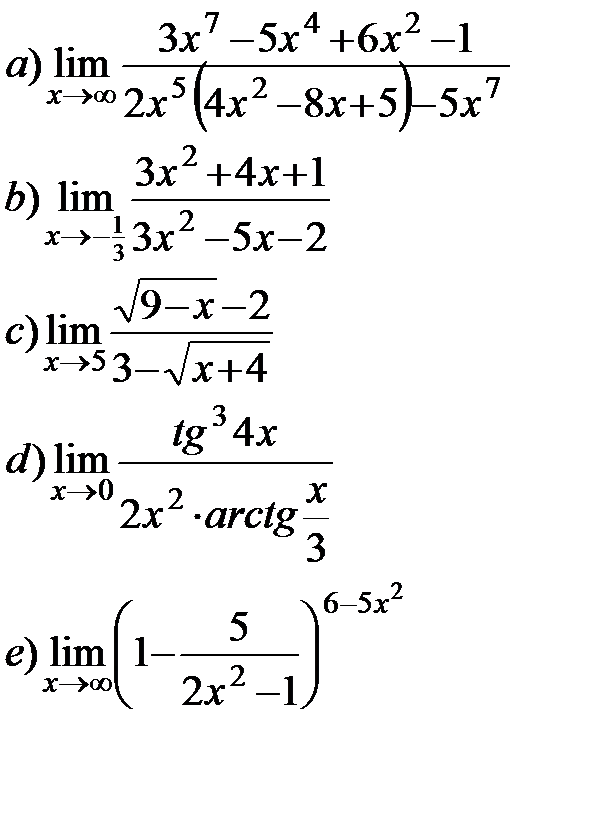
| + |
| + |
| + |
| 8 |
| 5 |
| + |
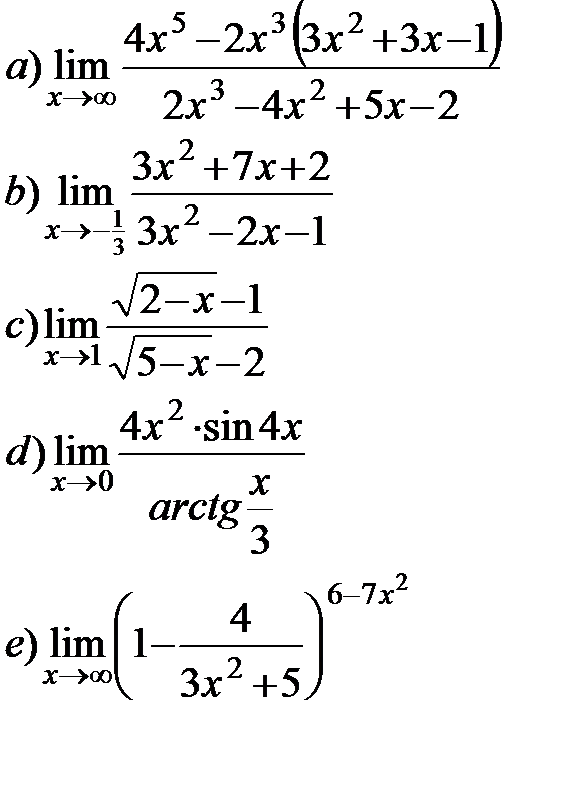 11.8.
11.8. 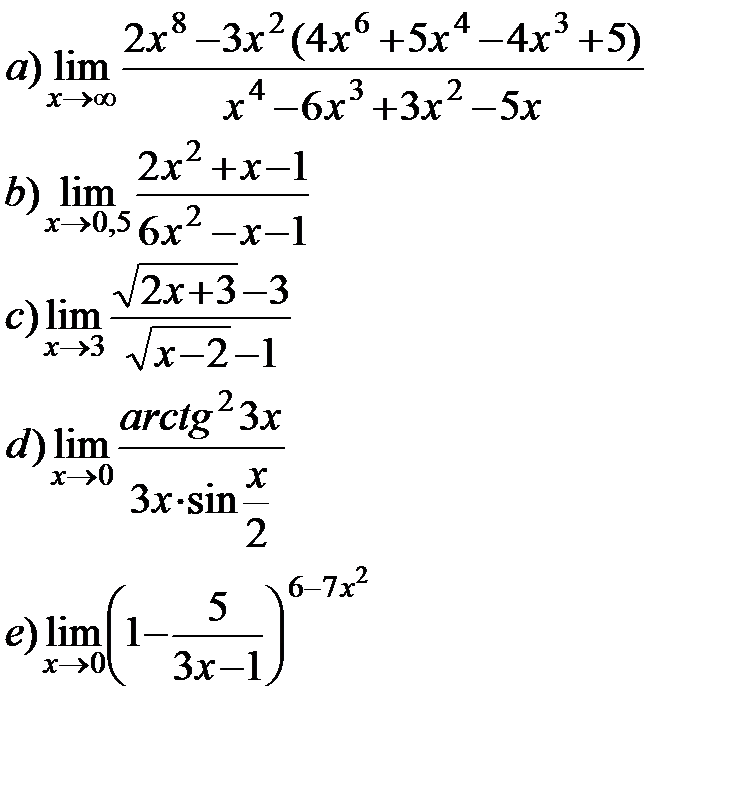
11.9.  11.10.
11.10. 
11.11.  11.12.
11.12. 
| + |
| 5 х+ 3 |
| (4 |
| 3 х –7 |
| 2 х –4 |
| + |
| 7 |
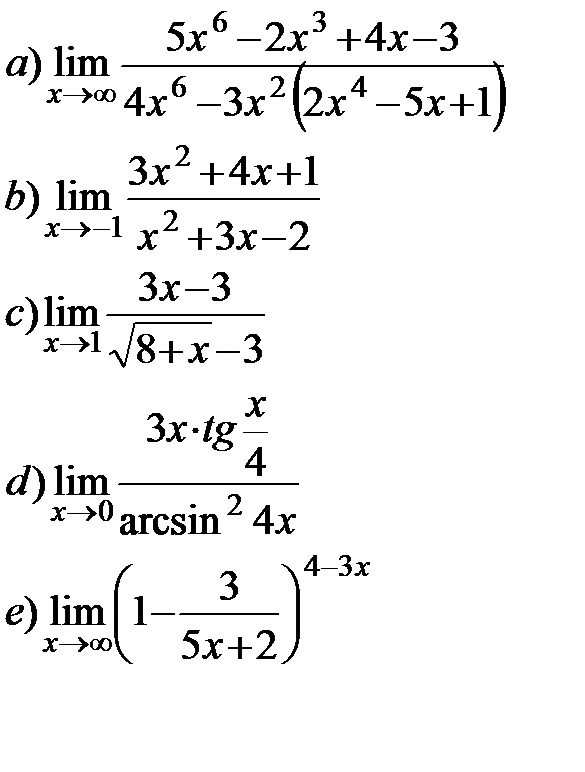 11.14.
11.14. 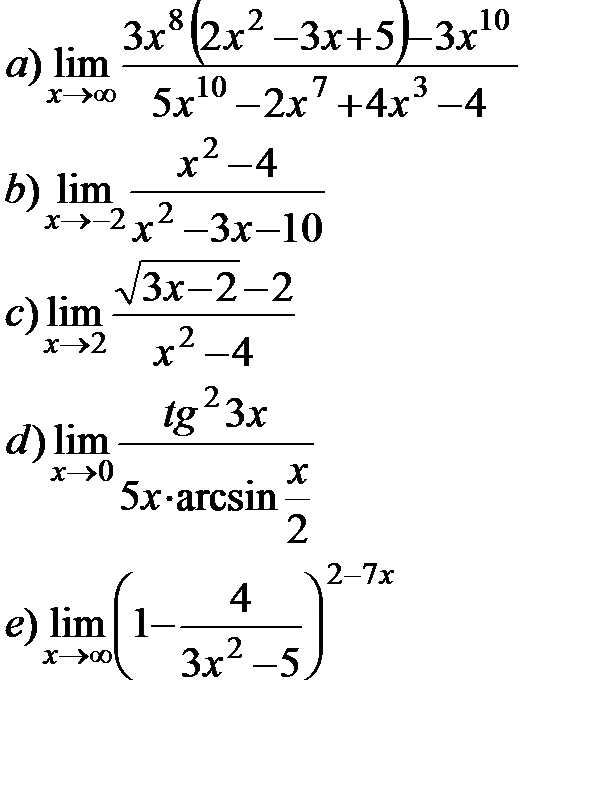
11.15.  11.16.
11.16. 
11.17. 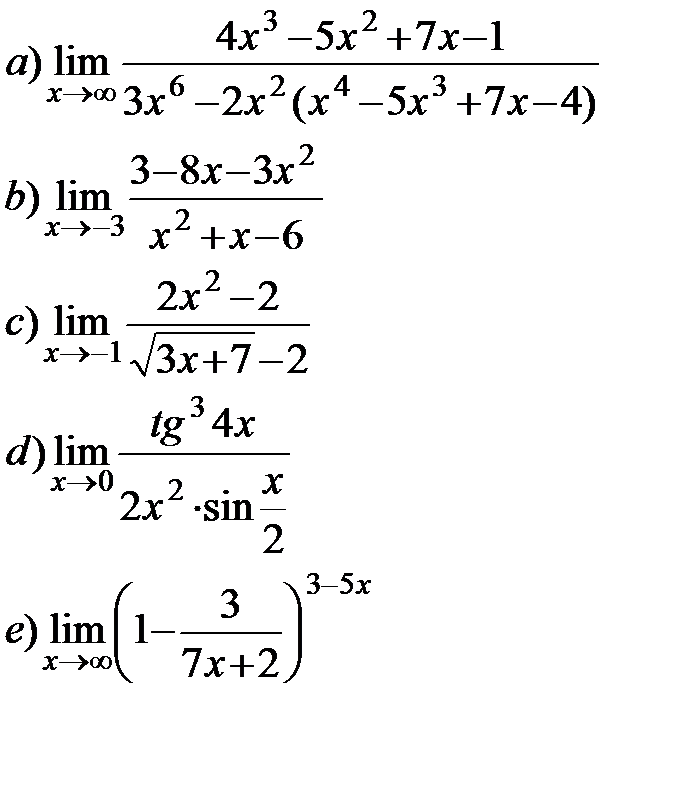 11.18.
11.18. 
| 4 х –2 |
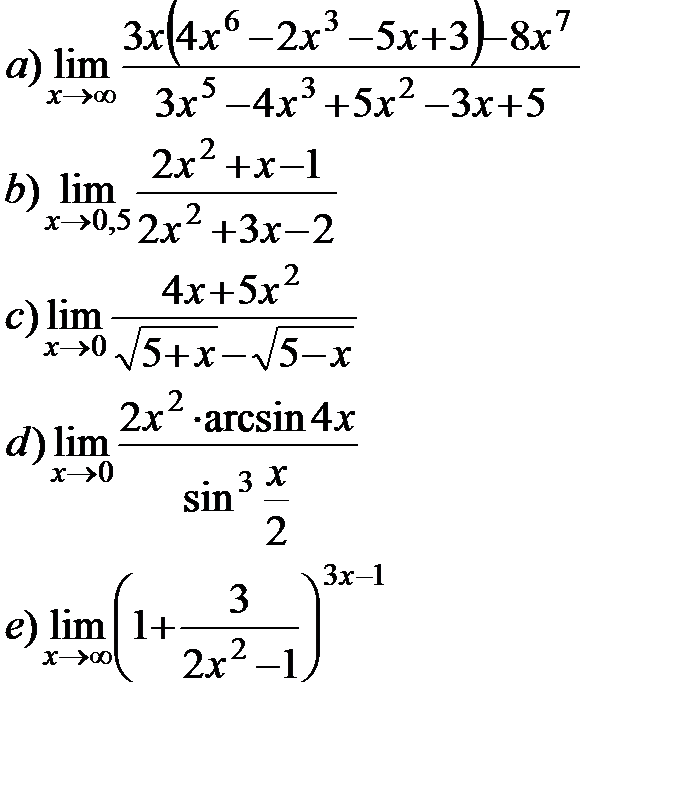 11.20.
11.20. 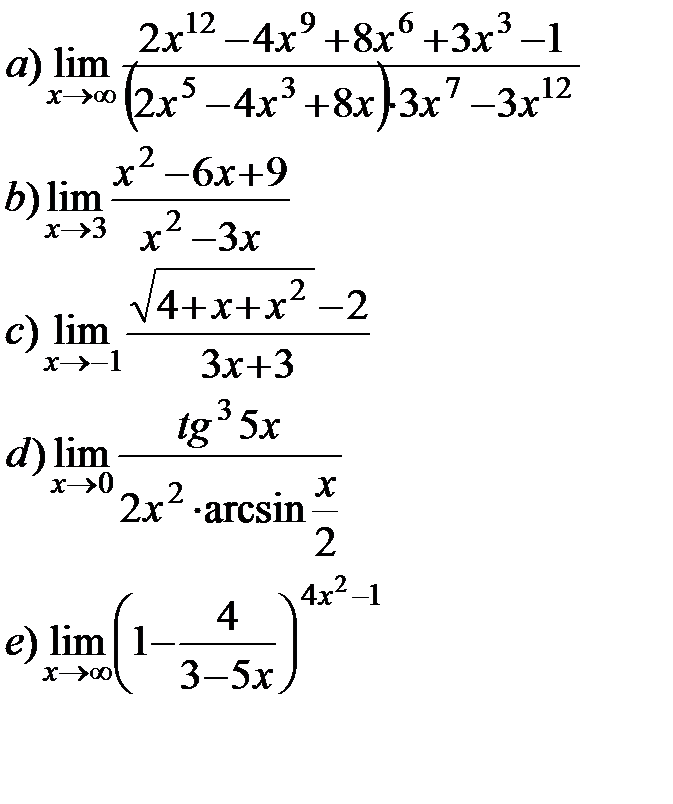
Дифференциальное исчисление функции одной переменной
В задачах 12.1 – 12.20 функция задана явно (пункты а, b), неявно (пункт c) и параметрически (пункт d). Найдите производную y' каждой из данных функций.


12.1.  12.2.
12.2. 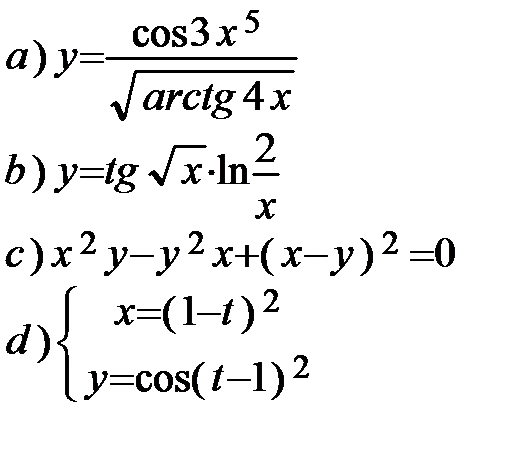
12.3.  12.4.
12.4. 
12.5.  12.6.
12.6. 
12.7.  12.8.
12.8. 
12.9.  12.10.
12.10. 
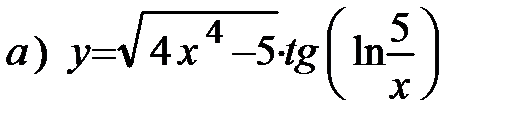 12.11.
12.11.  12.12.
12.12. 
12.13.  12.14.
12.14. 
12.15.  12.16.
12.16. 
12.17.  12.18.
12.18. 
12.19.  12.20.
12.20. 
В задачах 13.1 – 13.20 найдите вторую производную данной функции в заданной точке  .
.
13.1  13.2
13.2 
13.3  13.4
13.4 
13.5  13.6
13.6 
13.7  13.8
13.8 
13.9  13.10
13.10 
13.11 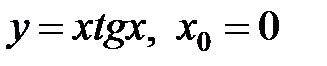 13.12
13.12 
13.13 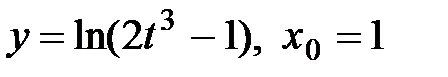 13.14
13.14 
13.15  1 13.16
1 13.16 
13.17 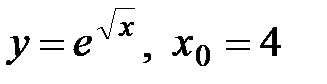 13.18
13.18 
13.19.  13.20.
13.20. 
В задачах 14.1 – 14.20 исследуйте данную функцию и постройте её график.
Схема исследования функции:
1. Найдите область определения функции.
2. Исследуйте функцию на чётность.
3. Исследуйте функцию на непрерывность и определите характер точек разрыва, если они есть.
4. Определите асимптоты графика функции.
5. Найдите точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.
6. Определите интервалы монотонности функции и экстремумы.
7. Найдите интервалы выпуклости, вогнутости графика функции и точки перегиба.
8. Используя результаты, полученные в пунктах 1 – 7, постройте график функции. В случае необходимости найдите дополнительно несколько точек графика непосредственно по заданному уравнению.
14.1.  14.2.
14.2.  14.3.
14.3. 
14.4.  14.5.
14.5.  14.6.
14.6. 
14.7.  14.8.
14.8.  14.9.
14.9. 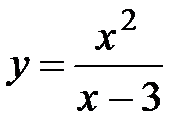
14.10.  14.11.
14.11. 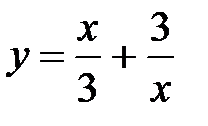 14.12.
14.12. 
14.13. 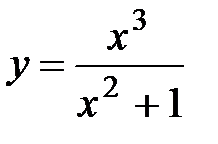 14.14.
14.14.  14.15.
14.15. 
14.16.  14.17.
14.17. 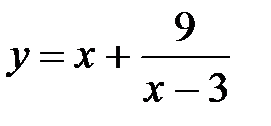 14.18.
14.18. 
14.19.  14.20.
14.20. 
Функции нескольких переменных
В задачах 15.1 – 15.20 найдите дифференциалы первого и второго порядков  и
и  данной функции
данной функции  .
.
15.1  15.2.
15.2.  15.3.
15.3. 
15.4.  15.5.
15.5.  15.6.
15.6. 
15.7.  15.8.
15.8.  15.9.
15.9. 
15.10.  15.11.
15.11.  15.12.
15.12. 
15.13. 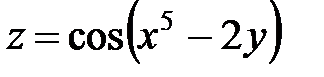 15.14.
15.14.  15.15.
15.15. 
15.16.  15.17.
15.17.  15.18.
15.18. 
15.19.  15.20.
15.20. 
В задачах 16.1-16.20 задана функция  . Исследуйте её на экстремум.
. Исследуйте её на экстремум.
16.1  .
.
16.2.  .
.
16.3 
16.4 
16.5. 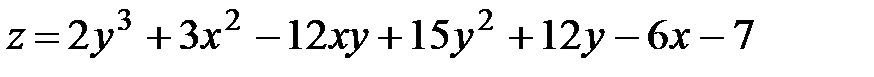 .
.
16.6.  .
.
16.7.  .
.
16.8.  .
.
16.9. 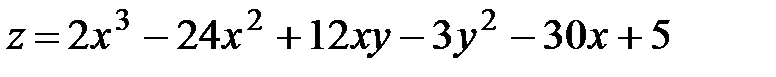 .
.
 16.10.
16.10.  .
.
16.11..
16.12.  .
.
16.13 
16.14 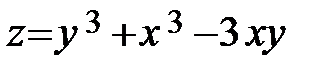
16.15.  .
.
16.16. 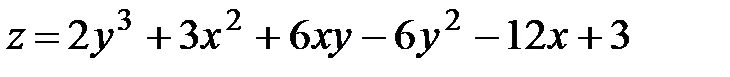 .
.
16.17.  .
.
16.18.  .
.
16.19. 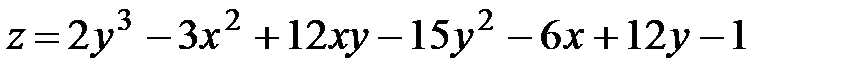 .
.
16.20.  .
.
Интегральное исчисление
В задачах 17.1-17.20 найдите неопределённые интегралы.
17.1 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.2 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.3 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.4 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.5. а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.6 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.7 а) 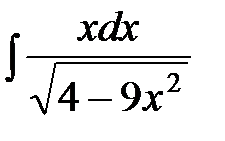 ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.8 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.9 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.10 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 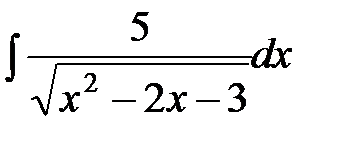
17.11 а)  ; b)
; b) 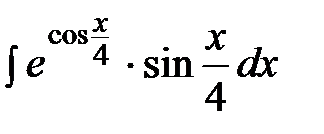 ; с)
; с)  ; d)
; d) 
17.12 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.13 а)  ; b)
; b)  ; с)
; с) 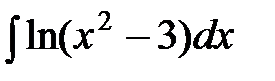 ; d)
; d) 
17.14 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.15 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.16 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 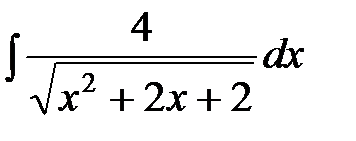
17.17 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.18 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.19 а)  ; b)
; b)  ; с)
; с)  ; d)
; d) 
17.20 а)  ; b)
; b) 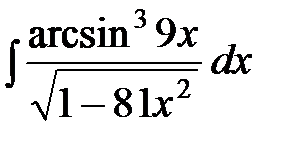 ; с)
; с) 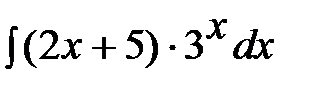 ; d)
; d) 
В задачах 18.1 (а) – 18.20 (а) вычислите определённые интегралы с помощью метода замены переменной.
В задачах 18.1 (б) – 18.20 (б) вычислите определённые интегралы сначала по формуле Ньютона-Лейбница, а затем приближённо по формулам прямоугольников, трапеций, Симпсона, разбив отрезок интегрирования на 10 равных частей. Все вычисления производите с округлёнными до третьего десятичного знака числами. Сравните полученные значения интеграла.
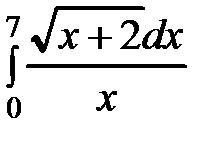 б)
б) 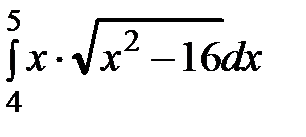
18.2 а)  б)
б) 
18.3 а)  б)
б) 
18.4 а)  б)
б) 
18.5 а)  б)
б) 
18.6 а)  б)
б) 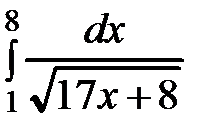
18.7 а) 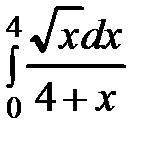 б)
б) 
18.8 а)  б)
б) 
18.9 а)  б)
б) 
18.10 а)  б)
б) 
18.11 а)  б)
б) 
18.12 а) 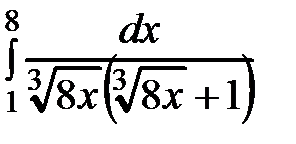 б)
б) 
18.13 а)  б)
б) 
18.14 а)  б)
б) 
18.15 а)  б)
б) 
18.16 а)  б)
б) 
18.17 а)  б)
б) 
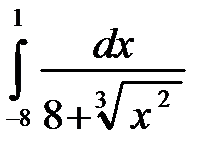 б)
б) 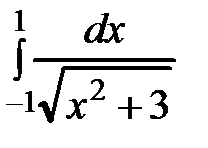
18.19 а)  б)
б) 
18.20 а) 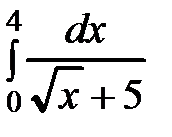 б)
б) 
В задачах 19.1 (а) – 19.20 (а) с помощью определённого интеграла вычислите площадь, ограниченную заданными линиями. Сделайте чертёж.
В задачах 19.1 (б) – 19.20 (б) фигура, ограниченная заданными линиями, вращается вокруг одной из осей координат. Найдите объём тела вращения. Сделайте чертёж.
19.1 а) 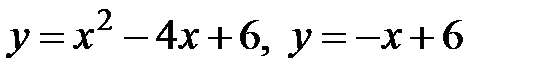 б)
б) 
(Вращение вокруг оси Оу)
19.2 а) 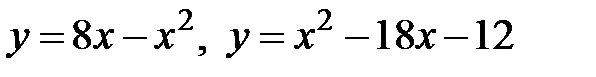 б)
б) 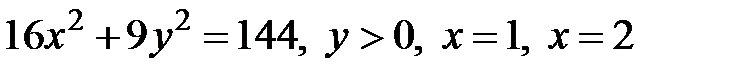
(Вращение вокруг оси Ох)
19.3 а)  б)
б) 
(Вращение вокруг оси Оу)
19.4 а)  б)
б) 
(Вращение вокруг оси Ох)
19.5 а)  б)
б) 
(Вращение вокруг оси Оу)
19.6 а)  б)
б) 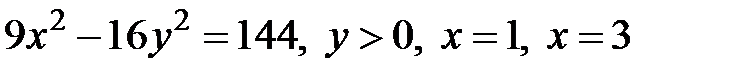
(Вращение вокруг оси Ох)
19.7 а)  б)
б) 
(Вращение вокруг оси Оу)
19.8 а)  б)
б) 
(Вращение вокруг оси Ох)
19.9 а) у 2 = 1 – х, у = х +1 б) 
(Вращение вокруг оси Оу)
19.10 а)  б)
б) 
(Вращение вокруг оси Ох)
19.11 а)  б)
б) 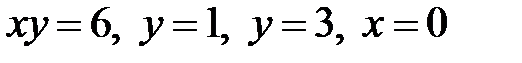
(Вращение вокруг оси Оу)
19.12 а)  б)
б) 
(Вращение вокруг оси Ох)
19.13 а)  б)
б) 
(фигура расположена в (Вращение вокруг оси Оу)
первой четверти)
19.14 а)  б)
б) 
(Вращение вокруг оси Ох)
19.15 а)  б)
б) 
(Вращение вокруг оси Оу)
19.16 а) 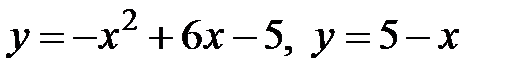 б)
б) 
(Вращение вокруг оси Ох)
19.17 а) 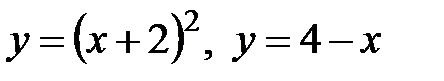 б)
б) 
(Вращение вокруг оси Оу)
19.18 а)  б)
б) 
(Вращение вокруг оси Ох)
19.19 а)  б)
б) 
(Вращение вокруг оси Оу)
19.20 а)  б)
б) 
(Вращение вокруг оси Ох)
В задачах 20.1-20.20 найдите несобственные интегралы или докажите их расходимость.
| + |
| + |
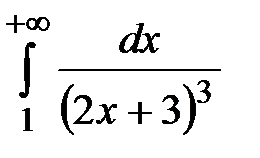 20.2
20.2 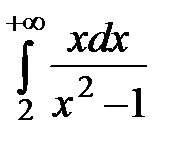 20.3
20.3 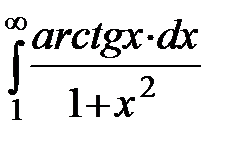 20.4
20.4 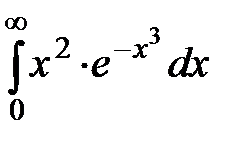
| + |
| + |
| + |
| + |
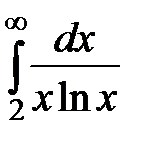 20.6
20.6 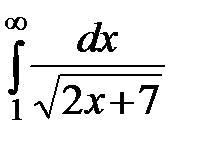 20.7
20.7 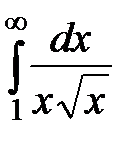 20.8
20.8 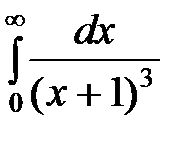
| + |
| + |
| + |
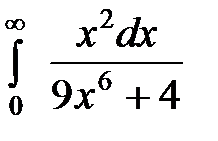 20.10
20.10 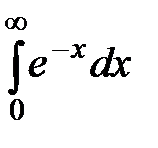 20.11
20.11 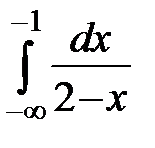 20.12
20.12 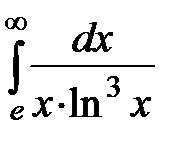
| + |
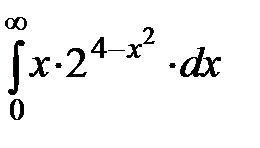 20.14
20.14 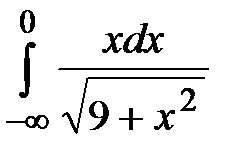 20.15
20.15 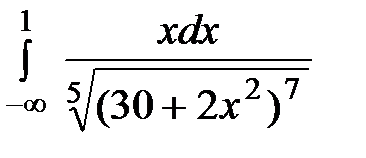
20.16 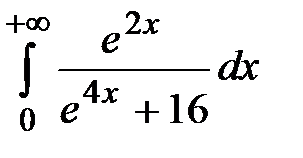 20.17
20.17  20.18
20.18  ;
;
| + |
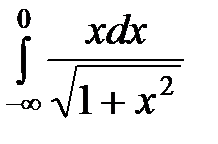 20.20
20.20