Если ряд  сходится, то его n -ый член при неограниченном возрастании номера n стремится к нулю, т.е.
сходится, то его n -ый член при неограниченном возрастании номера n стремится к нулю, т.е.  сходится Þ
сходится Þ  .
.
Достаточный признак сходимости ряда.
Если n -ый член ряда при неограниченном возрастании его номера n не стремится к нулю, то этот ряд расходится: 
 - расходится.
- расходится.
Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно Сделайте после дополнительного исследования.
Пример 81. Установить выполняется ли необходимое условие сходимости ряда: 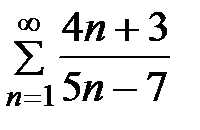 .
.
Решение.  , т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится.
, т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится.
Достаточные признаки сходимости рядов с положительными членами
Признак сравнения (предельная форма)
Если  и
и  два ряда с положительными членами и существует конечный предел отношения их общих членов, отличный от нуля, то ряды одновременно сходятся или расходятся:
два ряда с положительными членами и существует конечный предел отношения их общих членов, отличный от нуля, то ряды одновременно сходятся или расходятся:  ведут себя одинаково.
ведут себя одинаково.
Замечание. Признак сравнения, в основном, следует применять к тем знакоположительным рядам, у которых общий член представляет собой отношение двух многочленов.
При исследовании рядов на сходимость с помощью признака сравнения необходимо иметь ряды, сходимость или расходимость которых заранее известна, т.е. так называемые “эталонные ряды”, представлены в таблице15.
Таблица15 – Эталонные ряды
| Вид ряда | Название ряда | Поведение ряда |

| Гармонический | Расходится |

| Обобщенный гармонический (или ряд «р») | При р > 1 - сходится, при р £ 1 -расходится |

| Ряд, члены которого образуют геометрическую прогрессию | При 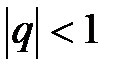 - сходится, при - сходится, при  - расходится - расходится
|
Пример 82. Используя признаки сравнения, исследовать на сходимость следующий ряд:  .
.
Решение.  .
.
Применим к э тому ряду предельный признак сравнения, обозначив общий член исследуемого ряда как  .
.
В качестве «эталонного» ряда возьмем обобщенный гармонический ряд
с общим членом  .
.
Применяя предельную форму признака сравнения, найдём предел отношения
 :
: 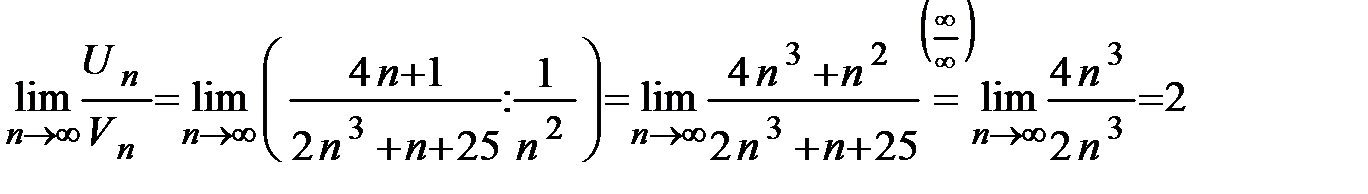 .
.
Предел конечен и отличен от нуля, следовательно, на основании предельного признака сравнения заключаем, что исследуемый ряд  и «эталонный» ряд
и «эталонный» ряд  ведут себя одинаково. «Эталонный» ряд сходится, поэтому исследуемый ряд тоже сходится.
ведут себя одинаково. «Эталонный» ряд сходится, поэтому исследуемый ряд тоже сходится.
Признак Даламбера
Если для знакоположительного ряда  существует предел отношения последующего члена к предыдущему при неограниченном возрастании номера n, т.е.
существует предел отношения последующего члена к предыдущему при неограниченном возрастании номера n, т.е.  , то при
, то при  - ряд сходится, а при
- ряд сходится, а при  - расходится.
- расходится.
Замечания. 1. Если  , то ряд также расходится.
, то ряд также расходится.
2. Если  , то признак Даламбера ответа о сходимости ряда не дает (т.е. ряд может быть как сходящимся, так и расходящимся). В этом случае рекомендуется перейти к другим достаточным признакам.
, то признак Даламбера ответа о сходимости ряда не дает (т.е. ряд может быть как сходящимся, так и расходящимся). В этом случае рекомендуется перейти к другим достаточным признакам.
Признак Даламбера удобно применять для тех рядов, у которых общий член содержит степени, факториалы, нарастающие произведения.
Пример 83. Исследовать ряд на сходимость, применяя признак Даламбера:.  . Для нахождения последующего члена
. Для нахождения последующего члена  необходимо в общем члене заменить n на n +1:
необходимо в общем члене заменить n на n +1:
Решение. Общий член ряда равен: 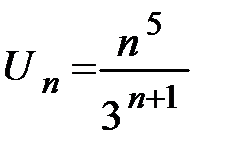 .
.  .
.
Так как 
 , то по признаку Даламбера ряд сходится.
, то по признаку Даламбера ряд сходится.