Если ищется предел функции  при условии, что аргумент x, стремясь к своему предельному значению х0, может принимать только такие значения, которые меньше х0, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке
при условии, что аргумент x, стремясь к своему предельному значению х0, может принимать только такие значения, которые меньше х0, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке  и обозначается так:
и обозначается так:  , или
, или  .
.
Если ищется предел функции  при условии, что аргумент x, стремясь к своему предельному значению х0, может принимать только такие значения, которые больше х0, то этот предел, если он существует, называется правосторонним (правым) пределом данной функции в точке
при условии, что аргумент x, стремясь к своему предельному значению х0, может принимать только такие значения, которые больше х0, то этот предел, если он существует, называется правосторонним (правым) пределом данной функции в точке  и обозначается так:
и обозначается так: 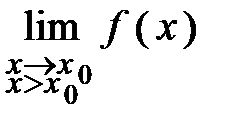 , или
, или 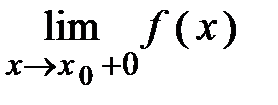 .
.
Наличие конечных односторонних пределов связано с существованием предела в рассматриваемой точке: предел функции  в точке х0 существует и равен числу а, если существуют равные этому же числу односторонние пределы.
в точке х0 существует и равен числу а, если существуют равные этому же числу односторонние пределы.
Наиболее важным классом функций является класс непрерывных функций. Понятие непрерывности функции тесно связано с геометрическим изображением функции – её графиком.
Очевидно, что непрерывность функции в данной точке выражается непрерывностью её графика при прохождении данной точки (без отрыва карандаша от листа бумаги).
Определение. Функция  непрерывна в точке
непрерывна в точке 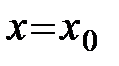 , если выполняются следующие условия: 1) функция
, если выполняются следующие условия: 1) функция  определена в точке х0, т.е. существует
определена в точке х0, т.е. существует 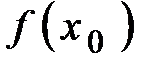 ;
;
2) функция  имеет при
имеет при  конечные и равные между собой односторонние пределы;
конечные и равные между собой односторонние пределы;
3) односторонние пределы при  совпадают со значением функции в точке х0, т.е.
совпадают со значением функции в точке х0, т.е.  .
.
Если для данной функции  в точке
в точке  хотя бы одно из перечисленных трёх условий не выполняется, то функция называется
хотя бы одно из перечисленных трёх условий не выполняется, то функция называется
разрывной в точке  , а точка х0 - точкой разрыва.
, а точка х0 - точкой разрыва.
Точка  называется точкой разрыва первогорода, если односторонние пределы функции слева и справа в этой точке существуют, но не равны между собой (неустранимый разрыв) или равные односторонние пределы не совпадают со значением функции в данной точке (устранимый разрыв).
называется точкой разрыва первогорода, если односторонние пределы функции слева и справа в этой точке существуют, но не равны между собой (неустранимый разрыв) или равные односторонние пределы не совпадают со значением функции в данной точке (устранимый разрыв).
Если же хотя бы один из односторонних пределов функции в точке  не существует или равен бесконечности, то точка
не существует или равен бесконечности, то точка  называется точкой разрыва второгорода. Всё это время мы говорили о непрерывности функции y = f(x) в точке
называется точкой разрыва второгорода. Всё это время мы говорили о непрерывности функции y = f(x) в точке  . Введём определение непрерывности функции на интервале.
. Введём определение непрерывности функции на интервале.
Определение. Функция y = f(x) называется непрерывной на интервале (a,b), если она непрерывна в каждой точке этого интервала.
Можно доказать, что все основные элементарные функции непрерывны при всех значения х, для которых они определены. Сформулируем теорему, позволяющую исследовать функцию на непрерывность.
Теорема: Всякая элементарная функция непрерывна в своей области определения.
| х |
| у |
| -1 |
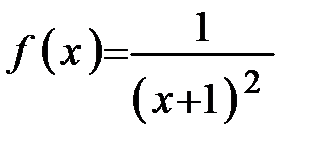
на непрерывность, т.е. найти точки разрыва
если они есть; и установить характер точек разрыва.
Сделайте схематический чертёж.
Решение. Находим область определения функции:  .
.  . Рисунок 34
. Рисунок 34
Функция непрерывна на всей числовой оси, кроме  . Точка
. Точка 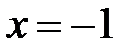 - точка разрыва. Определим характер точки разрыва. Найдём односторонние пределы в этой точке:
- точка разрыва. Определим характер точки разрыва. Найдём односторонние пределы в этой точке: 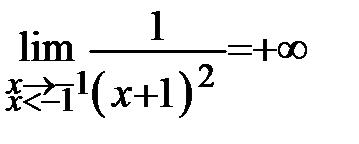 , так как знаменатель стремится к нулю, оставаясь положительным;
, так как знаменатель стремится к нулю, оставаясь положительным;  , так как знаменатель стремится к нулю, оставаясь положительным. Следовательно, х=-1 точка разрыва II рода (рисунок 34).
, так как знаменатель стремится к нулю, оставаясь положительным. Следовательно, х=-1 точка разрыва II рода (рисунок 34).