Определение. Смешанным произведением трёх векторов 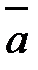 ,
, 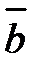 ,
, 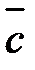 называется их векторно – скалярное произведение:
называется их векторно – скалярное произведение:
(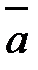

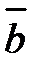 )·
)· 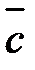 , которое обозначается
, которое обозначается 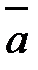
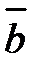
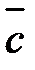 .
.
Если некомпланарные векторы 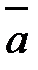 ,
, 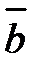 ,
, 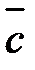 приведены к общему началу, то абсолютная величина ихсмешанного произведения равна объёму параллелепипеда, построенного на этих векторах как на рёбрах (рисунок 2).
приведены к общему началу, то абсолютная величина ихсмешанного произведения равна объёму параллелепипеда, построенного на этих векторах как на рёбрах (рисунок 2).
 V = |
V = | 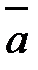
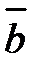
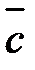 |. (2.10)
|. (2.10)
Три ненулевых вектора компланарны (т.е. лежат
 Н в одной плоскости или в параллельных плоско-
Н в одной плоскости или в параллельных плоско-
 стях) тогда и только тогда, когда их смешан-
стях) тогда и только тогда, когда их смешан-
ное произведение равно нулю, т.е
| Рисунок 2 |
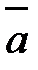
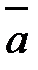 ,
, 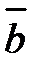 ,
, 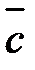 - компланарны
- компланарны 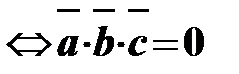 (2.11)
(2.11)
Пусть векторы 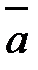 ,
, 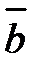 и
и 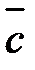 заданы своими координатами:
заданы своими координатами: 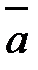 =
=  ,
,
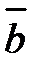 =
= 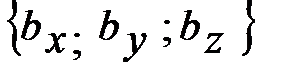 и
и 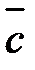
 .
.
Тогда смешанное произведение 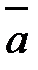
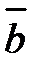
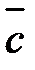 равно определителю третьего порядка, составленному из координат векторов
равно определителю третьего порядка, составленному из координат векторов 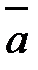 ,
, 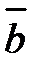 ,
, 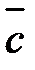 :
:
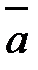
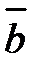
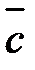 =
=  . (2.12)
. (2.12)
Пример 15. Найти объём треугольной пирамиды с вершинами в точках
А(-1; 1; 0), В (2; -2; 1), С(3; 1; -1) и D(1; 0; -2).
Решение. Рассмотрим векторы 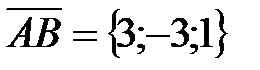 ,
,  и
и 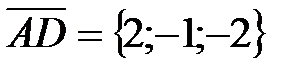 . Из школьного курса геометрии известно, что искомый объём пирамиды равен 1/6 объёма параллелепипеда, построенного на векторах
. Из школьного курса геометрии известно, что искомый объём пирамиды равен 1/6 объёма параллелепипеда, построенного на векторах 
 и
и  (рисунок 3).
(рисунок 3).
По формуле (2.12) найдём смешанное произведение векторов  ,
,  ,
,  :
:

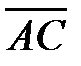
 =
=  =
= 
 .
.
Рисунок 3 Тогда,  (куб. ед.)
(куб. ед.)
Ответ: 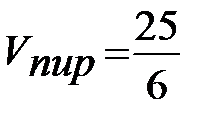 (куб. ед.).
(куб. ед.).
| D |
| Рисунок 4 |
| С |
| В |
| А |
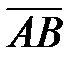 ,
, 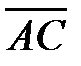 и
и 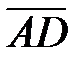 компланарны (рисунок 4). Учитывая условие компланарности (2.11) необходимо убедиться в том, что смешанное произведение образованных векторов равно нулю:
компланарны (рисунок 4). Учитывая условие компланарности (2.11) необходимо убедиться в том, что смешанное произведение образованных векторов равно нулю: 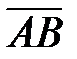
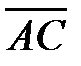
 = 0. Сделайте это самостоятельно.
= 0. Сделайте это самостоятельно.
Аналитическая геометрия на плоскости
Простейшие задачи
Если на плоскости задана прямоугольная декартова система координат ХОУ, то точку М этой плоскости, имеющую координаты х и у, обозначают М(х; у).
Расстояние d между точками М1(х1; у1) и М2(х2; у2) рассматривается как длина соответствующего вектора  и определяется по формуле:
и определяется по формуле:
 . (3.1)
. (3.1)
Разделить отрезок М1М2 в заданном отношении l>0 - это означает, найти точку С(х; у) такую, что  . (3.2)
. (3.2)
Если известны координаты концов отрезка, т.е. точки М1(х1; у1) и
М2(х2; у2), то координаты точки С(х; у), определяемой соотношением (3.2), находятся по формулам:
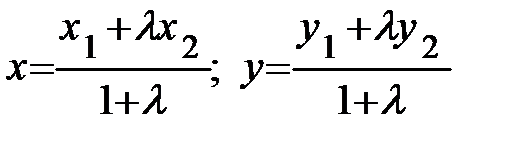 . (3.3)
. (3.3)
В частности, при l=1 получаем формулы для координат середины отрезка М1М2:  . (3.4)
. (3.4)
Понятие о методе координат
В аналитической геометрии изучаются геометрические объекты аналитическими методами. Основным методом изучения является метод координат. Схематически этот метод состоит в следующем.
Геометрический объект рассматривается в системе координат (на плоскости или в пространстве). Текущей точкой называют такую точку, которая меняется на изучаемом объекте. Эта точка не может иметь произвольные координаты, её координаты обязательно связаны так, чтобы точка не сходила с объекта. По имеющимся геометрическим описаниям (определениям) объекта устанавливаются связи (или связь) между координатами текущей точки. Эти связи или связь называют уравнениями или уравнением геометрического объекта. После получения уравнений их изучают, а затем делают выводы о самом объекте.
Прямая на плоскости
Прямая – один из неопределяемых геометрических объектов. Однако, имеются различные описания прямой. Пользуясь ими, можно доказать следующее утверждение.
Теорема. Всякое уравнение первой степени относительно текущих
координат х и у  , (3.5)
, (3.5)
где А и В одновременно не равны нулю, определяет прямую в декартовой системе координат и наоборот, всякой прямой соответствует уравнение вида (3.5).
В связи с этим, уравнение (3.5) называется общим уравнением прямой.
Пример 17. Построить прямую 2 х – 3 у + 6 = 0.
Решение. Для построения прямой достаточно знать какие – либо две её точки, например, точки её пересечения с осями координат.
у с ОХ: полагаем у = 0, имеем 2 х + 6 = 0
или х = -3, т.е. А (-3; 0);
2 В с ОУ: полагаем х = 0, тогда - 3 у + 6 = 0
| b |
| j |
А Строим прямую, проходящую через
-3 0 х найденные точки А и В (рисунок 5).
Рисунок 5
Если общее уравнение прямой (3.5) привести к виду:
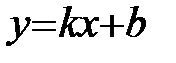 , (3.6)
, (3.6)
то получим уравнение прямой с угловым коэффициентом k, который определяется как тангенс угла наклона j этой прямой к оси Ох т.е. k = tgφ, b = ОВ - начальная ордината (рисунок 5).
Если известна точка А (х0; у0), лежащая на прямой, и угловой коэффициент k, то уравнение прямой записывается в виде:
у – у0 = k · (х – х0). (3.7)
Уравнение (3.7) называют уравнением прямой, проходящей через заданную точку в данном направлении или уравнением пучка прямых.
Если известны две точки М1(х1; у1) и М2 (х2; у2), лежащие на прямой, то уравнение можно записать в виде:
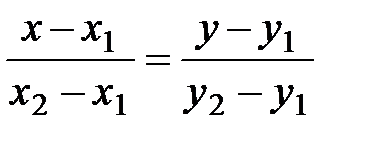 . (3.8)
. (3.8)
Уравнение (3.8) называют уравнением прямой, проходящей через две точки.
Условие параллельности двух прямых состоит в равенстве их угловых коэффициентов: k1 = k2, (3.9)
а условие перпендикулярности - в выполнении соотношения:
k1 · k2 = -1. (3.10)
Пример 18. Даны вершины треугольника АВС:  .
.
Требуется найти:
1) уравнения сторон АВ и АС и их угловые коэффициенты;
2) уравнение медианы АМ;
3) уравнение высоты СН;
4) уравнение прямой l, проходящей через вершину В параллельно стороне АС.
Сделайте чертёж.
Решение. 1) Для составления уравнений сторон АВ и АС воспользуемся уравнением (3.8). Подставляя в (3.8) координаты точек А и В, получаем: 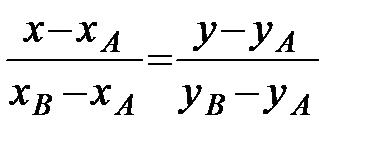 ;
;  ;
;  ;
;  ;
;  ;
; 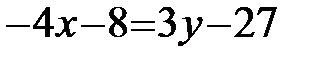 ; или
; или  (АВ).
(АВ).
Чтобы найти угловой коэффициент прямой АВ, решим полученное уравнение относительно y: 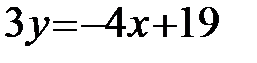 ;
;  , следовательно,
, следовательно,  . Аналогично, для составления уравнения стороны АС в (3.8) подставляем координаты точек
. Аналогично, для составления уравнения стороны АС в (3.8) подставляем координаты точек  и
и  . Имеем:
. Имеем: 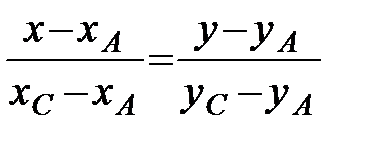 ;
;
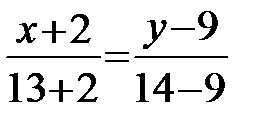 ;
;  ;
;  ;
;  или
или 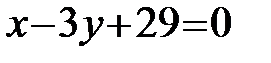 (АС).
(АС).
Находим угловой коэффициент прямой АС:  ;
;  ,
,
следовательно, 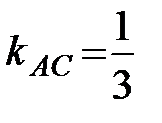 .
.
2) Для составления уравнения медианы АМ найдём координаты точки М, как середины стороны ВС, используя формулы деления отрезка пополам (3.4). Подставляя в (3.4) координаты точек В и С имеем: 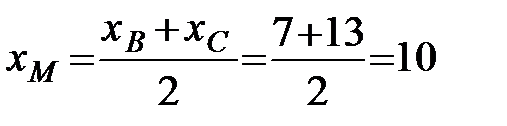 ;
; 
 . Зная координаты двух точек
. Зная координаты двух точек  и
и  , лежащих на медиане (АМ), и используя формулу (3.8), получим её уравнение:
, лежащих на медиане (АМ), и используя формулу (3.8), получим её уравнение:
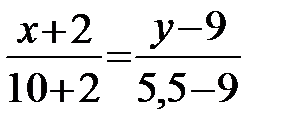 ;
;  ;
;  ;
;  ;
;
 (АМ).
(АМ).
3) Для того, чтобы найти уравнение высоты СН, воспользуемся уравнением пучка прямых (3.7). Так как  , то из условия перпендикулярности (3.10) имеем:
, то из условия перпендикулярности (3.10) имеем:  . Подставляя в (3.7) координаты точки С и значение углового коэффициента
. Подставляя в (3.7) координаты точки С и значение углового коэффициента  , получаем
, получаем 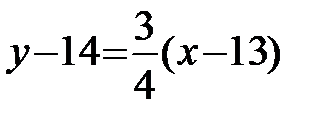 или
или  ,
,  или
или  (СН).
(СН).
| А |
| С |
| В |
| М |
| Н |
| l |
| x |
| y |
| –3 |
| –2 |
уравнением (3.7). Так как  // АС, то
// АС, то
 (воспользовались равенством (3.9)).
(воспользовались равенством (3.9)).
Подставляя в (3.7) координаты точки В и
значение углового коэффициента  , получаем:
, получаем:
 ;
;  ;
;  или
или
 (l). Строим чертёж. (рисунок 6)
(l). Строим чертёж. (рисунок 6)
Рисунок 6
Кривые второго порядка
Определение. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат х и у:
 , (3.11)
, (3.11)
где А, В, С, D, Е, F – действительные числа, при этом А, В, С не равны нулю одновременно. Уравнение (3.11) называется общим уравнением кривой второго порядка.
В зависимости от коэффициентов уравнение (3.11) определяет одну из четырёх кривых на плоскости: окружность, эллипс, гиперболу, параболу.
Окружность
Определение. Окружность – это множество точек плоскости, равноуда-
лённых от данной точки (центра).
Если R – радиус окружности, а точка  – её центр, то
– её центр, то
каноническое уравнение окружности имеет вид:
 . (3.12)
. (3.12)
В частности, если центр окружности совпадает с началом координат, то последнее уравнение примет вид: 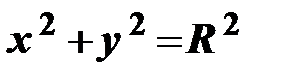 .
.
Выясним, при каких условиях общее уравнение кривой второго порядка (3.11) является уравнением окружности.
Для этого раскроем скобки в каноническом уравнении (3.12):
 , или
, или
 . (3.13)
. (3.13)
Чтобы уравнения (3.11) и (3.13) представляли одну и ту же линию, коэффициент С должен быть равен нулю (так как нет произведения 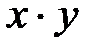 в (3.11)), а коэффициенты при квадратах переменных равны между собой:
в (3.11)), а коэффициенты при квадратах переменных равны между собой: 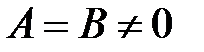 .
.
Тогда получаем уравнение:
 , (3.14)
, (3.14)
называемое общим уравнением окружности.
Пример 19. Построить кривую 9х2 + 9у2 – 72х + 18у + 117 = 0.
Так как в данном уравнении коэффициенты при квадратах переменных равны между собой и отсутствует произведение 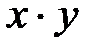 , то это уравнение определяет окружность.
, то это уравнение определяет окружность.
 Решение. Приведём данное уравнение к каноническому уравнению вида (3.12). Для этого разделим все его члены на 9, а затем сгруппируем отдельно члены, содержащие х и у:
Решение. Приведём данное уравнение к каноническому уравнению вида (3.12). Для этого разделим все его члены на 9, а затем сгруппируем отдельно члены, содержащие х и у:
(х2 – 8х) + (у2 + 2у) + 13 = 0. Дополним выражения,
стоящие в каждой из скобок, до полного квадрата
используя формулу сокращённого умножения
 :
:
(х2 – 2·х·4 + 42)- 42 + (у2 + 2·у·1 + 12) – 12 + 13 = 0 Рисунок 7
или (х – 4)2 + (у + 1)2 – 4=0, откуда (х – 4)2 + (у + 1)2 =4.
Сравнивая это уравнение с уравнением (3.11), получим координаты центра и радиус окружности:  и
и  . Строим окружность(рисунок 7).
. Строим окружность(рисунок 7).
Эллипс
Определение. Эллипс - это множество точек плоскости, сумма расстояний которых до двух фиксированных точек  и
и 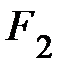 , называемых фокусами, есть величина постоянная и равная 2а.
, называемых фокусами, есть величина постоянная и равная 2а.
Уравнение  (3.15)
(3.15)
называется каноническим уравнением эллипса, где (х, у) – координаты текущей точки; а - большая полуось, b – малая полуось.
Точки А1 (- а; 0) и А2 (а; 0), В1 (0;- b) и В2 (0; b) - точки пересечения
эллипса с его осями симметрии (координатными осями), называются вершинами эллипса. Отрезки А1А2 и В1В2, длины которых соответственно равны 2а и 2b, называются соответственно большой и малой осями эллипса. Расстояние между фокусами F1 и F2 обозначается 2 с.
Если в уравнении эллипса (3.15) а > b (рисунок 8), то  , а фокусы имеют координаты: F1 (-c; 0) и F2(с; 0).
, а фокусы имеют координаты: F1 (-c; 0) и F2(с; 0).
Если же а < b ( рисунок 9), то  , F1 (0; -с) и F2(0; с).
, F1 (0; -с) и F2(0; с).

Рисунок 8 Рисунок 9
Пример 20. Построить эллипс 9 х 2 + 25 у 2 – 225 = 0.
 Решение. Приведём данное уравнение к
Решение. Приведём данное уравнение к
каноническому виду (3.15), для чего
свободный член уравнения перенесём
вправо и затем разделим на него все
члены уравнения. Получим  .
.
Откуда а 2=25Þ а =5 – большая полуось;
b 2 =9Þ b =3 – малая полуось. Рисунок 10
Координаты вершин эллипса А1 (-5;0), А2 (5;0), В1 (0; -3) и В 2 (0; 3).
Так как а>b, то с2=а2 - b2 = 25 – 9=16  с=4 и фокусы имеют координаты F 1(-4;0) и F 2(4;0) (рисунок 10).
с=4 и фокусы имеют координаты F 1(-4;0) и F 2(4;0) (рисунок 10).
Форму эллипса характеризует число  , называемое эксцентриситетом. Для эллипса
, называемое эксцентриситетом. Для эллипса  .
.
Гипербола
Определение. Гиперболой называется множество точек плоскости, разность расстояний которых до двух фиксированных точек F 1 и F 2, называемых фокусами, есть величина постоянная и равная ±2а.
Каноническое уравнение гиперболы имеет вид:
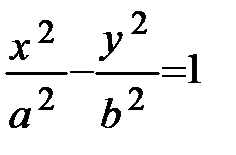 (3.16)
(3.16)
или  , (3.17)
, (3.17)
где 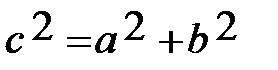 . (3.18)
. (3.18)
В формулах (3.16) – (3.17) (х, у) – координаты текущей точки, а - действительная полуось, b – мнимая полуось гиперболы.
Гипербола имеет две оси симметрии (координатные оси), с одной из которых она пересекается в двух точках, называемых вершинами. Вершины гиперболы и её фокусы расположены на действительной оси гиперболы.
Так, для гиперболы, заданной уравнением (3.16), отрезок A1A2 длиной 2а и расположенный на оси ОХ является действительной осью, точки А1(- а; 0) и А2 (а; 0) – вершинами, а точки F1 (- c; 0) и F2(с; 0) – фокусами (рисунок 11).
Для гиперболы, заданной уравнением (3.17), действительной осью является отрезок B1B2длиной 2b оси ОУ, вершинами – точки В1(0; - b) и
В2(0; b), а фокусами – точки F1 (0; -с) и F2(0; с) (рисунок 12).


Рисунок 11 Рисунок 12
Гипербола имеет две асимптоты, уравнения которых
 и
и  (3.19)
(3.19)
Форму гиперболы характеризует число  , называемое эксцентриситетом гиперболы. Для гиперболы
, называемое эксцентриситетом гиперболы. Для гиперболы  .
.
Пример 21. Построить гиперболу 9х2 – 16у2 - 144 = 0.
Решение. Перенесём свободный член вправо и разделим на него все члены данного уравнения. В результате получим каноническое уравнение гиперболы: 9х2 – 16у2 = 144, или  , или
, или  .
.
Сравнивая это уравнение с уравнением (3.16), имеем а = 4 - действительная полуось, b = 3 – мнимая полуось.
 Координаты вершин А1(-4;0) и А2(4;0). Для построения гиперболы построим прямоугольник с центром в начале координат и со сторонами 2а = 8 и 2b =6, проведём его диагонали и продолжим их. Эти прямые и есть асимптоты гиперболы и их уравнения:
Координаты вершин А1(-4;0) и А2(4;0). Для построения гиперболы построим прямоугольник с центром в начале координат и со сторонами 2а = 8 и 2b =6, проведём его диагонали и продолжим их. Эти прямые и есть асимптоты гиперболы и их уравнения:  и
и  .
.
Рисунок 13 По формуле (3.18) с2 = 16 + 9 = 25, с= 5. Тогда фокусы имеют координаты F1 (-5;0) и F2(5;0) (рисунок 13).
Парабола
Определение Параболой называется множество точек плоскости, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Величина р, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно её директрисе, называется осью.
Канонические уравнения параболы имеют вид:
у2 = 2рх (рисунок 14) (3.20) у2 = - 2рх (рисунок 15) (3.21)
х2 = 2ру (рисунок 16) (3.22) х2 = -2ру (рисунок 17) (3.23)
Вершины таких парабол расположены в начале координат, т.е. в точке О(0,0).

Рисунок 14 Рисунок 15 Рисунок16 Рисунок 17
Уравнение у = ах2 + bх + с (а  0) (3.24)
0) (3.24)
определяет параболу, ось которой параллельна оси ОУ, а вершина находится
в точке О1(х0; у0), где  , у0 = у(х0) (3.25)
, у0 = у(х0) (3.25)
Пример 22. Определить вид и построить кривую 24 х + 3 у2= 0.
Решение. Так как в данном уравнении одна переменная (х) входит в первой степени, а другая - (у), во второй, то оно определяет параболу. Приведём уравнение кривой к каноническому виду: 3у2 = - 24х, или у2 = - 8х. Сравнивая это уравнение с уравнением (3.21), находим, что 2р = 8, откуда  . Таким образом, точка F (-2; 0) – фокус параболы, а прямая х = 2 – её директриса. Для того, чтобы узнать размах ветвей, найдём пару точек, принадлежащих параболе: полагая х = -2 и подставляя это значение в каноническое уравнение параболы, имеем у2 = 16 Þ у =± 4 Þ А1(-2; 4) и А2 (-2; -4) (рисунок 18).
. Таким образом, точка F (-2; 0) – фокус параболы, а прямая х = 2 – её директриса. Для того, чтобы узнать размах ветвей, найдём пару точек, принадлежащих параболе: полагая х = -2 и подставляя это значение в каноническое уравнение параболы, имеем у2 = 16 Þ у =± 4 Þ А1(-2; 4) и А2 (-2; -4) (рисунок 18).
Пример 23. Определить вид и построить кривую 2 х2 - 4 х + 2 у – 6 =0.
Решение. Приведём уравнение к виду (3.24): у = - х 2 + 2 х + 3. Напомним построение параболы, заданной уравнением у = ах2+bx+c. В нашем примере
а = -1, b = 2, с = 3. Ось симметрии данной параболы параллельна оси Оу. Так как  , то ветви параболы направлены вниз. Найдём координаты вершины параболы, используя формулы (3.25):
, то ветви параболы направлены вниз. Найдём координаты вершины параболы, используя формулы (3.25):  ,
,  ,
,
у0 = у(1) = -12 +2 · 1 + 3 = 4  О1(1;4) - вершина. Затем найдём точки пересечения параболы с координатными осями. С ОХ: полагаем у = 0, имеем
О1(1;4) - вершина. Затем найдём точки пересечения параболы с координатными осями. С ОХ: полагаем у = 0, имеем
- х2 + 2х + 3 = 0, решая это уравнение, получим х1 = -1, х2 = 3 Þ В1 (-1; 0) и В2 (3; 0); с ОУ: полагаем х = 0, подставляя это значение в уравнение параболы, имеем у = 3 Þ С (0; 3). Отмечая на чертёже все найденные точки и соединяя их плавной кривой, построим искомую параболу (рисунок 19).

Рисунок 18 Рисунок 19
Пример 24. Составьте уравнение прямой, проходящей через центр окружности 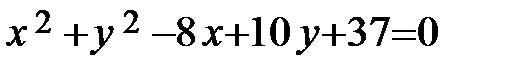 и левый фокус эллипса
и левый фокус эллипса  . Сделайте чертёж.
. Сделайте чертёж.
Решение. Чтобы узнать координаты центра окружности О 1, приведём уравнение к каноническому виду:  .
.
Сгруппируем члены, содержащие x и y:  .
.
Дополним выражения, стоящие в скобах, до полного квадрата:  или
или  .
.
Сравнивая полученное уравнение с уравнением (3.12), получим
О 1(4;–5) – центр окружности, R =2 – её радиус.
Для нахождения координат фокуса эллипса приведём его уравнение к
каноническому. Разделим обе части уравнения  на 400:
на 400:
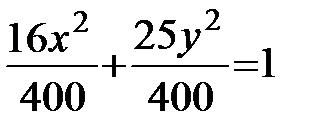 или
или  . Тогда имеем
. Тогда имеем 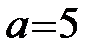 – большая полуось,
– большая полуось, 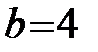 - малая полуось. Так как
- малая полуось. Так как  , то
, то  ,
,  .
.
| x |
| О1 |

|
| l |
| y |
 . Искомое уравнение прямой
. Искомое уравнение прямой  ищем в виде уравнения прямой, проходящей через две данные точки
ищем в виде уравнения прямой, проходящей через две данные точки  и
и 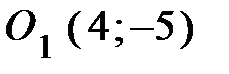 :
: 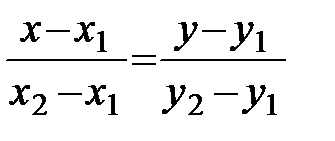 или
или 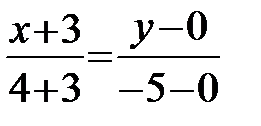 ;
; 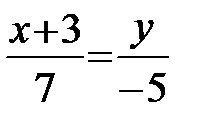 ;
; 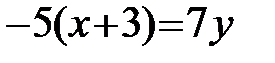 ;
; 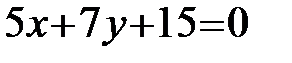 -
-  .
.
Рисунок 20 Сделаем чертёж (рисунок 20).