История развития алгебры

Знакомство с математикой (греч. mathêmatikê– наука, познание), и тем самым с алгеброй, обычно начинается с арифметики (греч. arithmos – число). Один из первых русских учебников, написанный Л.Ф. Магницким в 1707 г., начинался словами: «Арифметика или числительница есть художество честное, независтное и всем удобопонятное…». Арифметика изучает действия над числами, учит решать задачи, сводящиеся к арифметическим операциям: сложению, умножению, вычитанию и делению. Изучение свойств самих чисел составляет предмет теории чисел. Основные этапы развития арифметики: создание учения о величинах, числе, буквенного аппарата алгебры, разработка аксиоматической системы.

В современном изложении, арифметика – область знаний о числе и арифметических операциях в числовых множествах.

Арифметику можно представлять и как начальную ступень математики, на которой, когда возникла необходимость в поиске общих приемов решения однотипных арифметических задач, и появилась алгебра. Следует отметить и роль геометрии (как части математики, изучающей пространственные формы и телá) в становлении алгебры, появившейся, возможно, раньше арифметики. В III в. до н.э. древнегреческий ученый Евклид написал книгу «Начала», в которой пытался дать логически законченное аксиоматическое изложение геометрии; главы с седьмой по девятую (из двенадцати) Евклид посвятил арифметике.

В школьном курсе алгебры, после изучения алгебраических уравнений 1-й степени (линейных уравнений), выделяются два направления изучения предмета: решение квадратных и биквадратных уравнений и решение систем из двух или трех алгебраических уравнений.

Эти направления развивались и в высшей алгебре: «Алгебра многочленов одного или нескольких неизвестных» и «Линейная алгебра», исходной задачей которой являлось изучение систем линейных уравнений.

В первом случае следует отметить вклад Э. Галуа
(1811-1832). Работы Галуа содержали окончательное решение проблемы о разрешимости алгебраических уравнений в радикалах (1831). Сегодня это называется теорией Галуа [9] и составляет один из самых глубоко проработанных разделов алгебры.

Во втором случае исследование систем уравнений привело к созданию теории определителей, а затем и алгебры матриц. Появление теоремы Кронекера-Капелли (1883-1891) завершило построение общей теории систем линейных уравнений.

Оба направления оказались настолько плодотворными, что из них возникло несколько новых разделов алгебры, стимулируемых запросами, не только математическими, но и естественно научными дисциплинами.

Казалось, что развитие алгебры пойдет по традиционному пути. Будут искать новые классы уравнений, доказывать новые тождества и т.д., тем более что после создания комплексных чисел возникли гиперкомплексные числа [5], которые построил ирландский математик У. Гамильтон (1788-1856), но в середине XIX в. появилось понятие множества, а к его завершению, стараниями Б. Больцано (B. Bolzano) 1781-1848, Р. Дедекинда
(R. Dedekind) 1831-1916, Ф. Хаусдорфа (F. Hausdorff) 1868-1942 и, особенно, Г. Кантора (G. Cantor) 1845-1918, была создана теория множеств – учение о свойствах множеств элиминирующих (лат. eliminare – исключать, устранять) свойства элементов, из которых эти множества состоят [10].

Важным здесь оказались именно свойства множеств как носителя информации, а не его природа (т.е. его элементов). К свойствам множеств как объекта для алгебры относятся операции алгебраические и аналогичные им по смыслу, результат применения которых к элементам множества дает элемент того же множества.

Анализ применения арифметических операций (сложения, умножения, вычитания и деления) и арифметических действий (наибольшего общего делителя, наименьшего общего кратного и др.) на многочисленных примерах с числовыми множествами показал, что разумно использовать только сложение и умножение, а остальные рассматривать при необходимости их введения как свойства (аксиомы), дополнительные к свойствам (аксиомам) сложения и умножения.

Более того, оказалось, что и для нечисловых множеств (например, векторов или подобных треугольников) выполняются операции сложения и умножения не в смысле их обозначения или названий, а в содержательном смысле, представленном в виде свойств.

Так возникло абстрактное понятие операции композиции, как обобщение алгебраической операции.

Тем самым был осуществлен переход от алгебры первого уровня абстракции – использование вместо чисел букв при поиске общих приемов решения арифметических задач – к алгебре более высокого уровня абстракции: рассмотрение множеств, в которых носителями информации задаются операции композиции, каждая представленная в виде систем аксиом, которым удовлетворяют элементы множеств; остальные свойства элементов элиминируются (игнорируются).

Изучение системы аксиом, определяющих операцию композиции, привело к мысли, что можно изучать только их свойства независимо от объектов, к которым они применяются. Это означает, что два множества с заданными операциями, между которыми можно установить взаимно-однозначное соответствие и они удовлетворяют одной и той же системе аксиом, одинаковы. Такие множества называются изоморфными, т.е. обладающими одинаковыми свойствами. Другими словами, изучая одно из них, мы тем самым узнаем свойства другого.

Поскольку различных множеств с заданными в них операциями очень велико, то стали классифицировать множества хотя и не изоморфные, но обладающие общими свойствами частично. Классы таких множеств получили название алгебраической системы, т.е. системы, генерирующей множества с операциями (универсальные алгебры). Ясно, что алгебраическая система сама является универсальной алгеброй.

Например, изучив свойства операции умножения матриц, пришли к выделению понятия группы, одного из важнейших понятий не только как представителя универсальной алгебры
[2, 7], но и во всей математике. Другим примером универсальной алгебры является понятие поля – множества, для элементов которого определены две операции композиции: сложения и умножения для числовых множеств. Наиболее известны поля множеств рациональных чисел Q, действительных (вещественных) чисел R, комплексных чисел C, названия которых образованы от французских слов Quotient – отношение, Reel – действительный, Complex – комплексный. Название «поле» (числовое) своему появлению обязано аналогией с обычным полем – местностью, по которой можно двигаться без ограничений, не встречая никаких препятствий. Аксиомы поля подобраны так, чтобы в нем выполнялись не только арифметические операции, но и большинство других действий (в зависимости от конкретного числового множества).

Зададим поле аксиоматически. Так как каждое из перечисленных числовых множеств является полем, то, чтобы не связывать себя с числами из конкретных множеств, назовем элементы множеств скалярами (scalaris – ступенчатый) – величины, определяемые только своими числовыми значениями [2, 11].

Скалярное множество будем называть полем, если в нем заданы две бинарные операции композиции: сложение и умножение, удовлетворяющие аксиомам.

A. Для любых скаляров a, b, g из числового множества найдется скаляр , называемый суммой a и b, такой, что

1) сложение ассоциативно, т.е. ;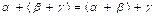

2) сложение коммутативно, т.е. ;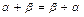

3) существует единственный скаляр 0 (нуль), такой, что ;

4) для любого a существует однозначно определенный скаляр (- a), такой, что .

B. Для любых скаляров a, b, g найдется скаляр (или ), называемый произведением a и b, такой, что

5) умножение ассоциативно, т.е. ;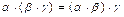

6) умножение коммутативно, т.е. ;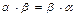

7) существует единственный ненулевой скаляр 1 (единица), такой, что для любого a, ;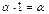

8) каждому ненулевому скаляру a соответствует однозначно определенный скаляр 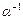, называемый обратным, такой, что .

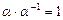C. Умножение дистрибутивно относительно сложения, т.е.

9) .

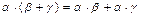Легко проверить, что множества Q, R, C удовлетворяют этим наборам аксиом. В дальнейшем в качестве основного будем рассматривать поле действительных чисел.

Среди других универсальных алгебр отметим а) решетки – множества с двумя бинарными операциями; например, решетку образует множество положительных рациональных чисел с операциями нахождения наименьшего общего кратного и наибольшего общего делителя; б) линейные пространства над числовым полем – множество с одной операцией – сложения и умножением на скаляры; в) множество с одной бинарной операцией, обычно называемой умножением (реже – сложением), удовлетворяющей системе аксиом B 1) – 4) поля, называется группой, а множество с двумя операциями называется кольцом.

Разберем универсальные алгебры подробно.

Группа

Пусть задано непустое множество G с одной алгебраической операцией композиции, обычно называемой умножением. Тогда для любых элементов a, b из G композиция записывается в виде и является элементом G.

Множество G называется группой [2, 11], если выполняются аксиомы

1) ;

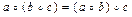2) существует единственный элемент 1, называемый нейтральным (для умножения это единица), такой, что

;

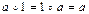3) существует единственный элемент 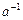, называемый обратным к произвольному элементу a группы, такой, что

,

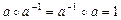если к тому же выполняется аксиома

4) ,

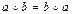то группа G называется абелевой или коммутативной.

Пример I.1. Подстановкой множества называется взаимно-однозначное отображение этого множества на себя по следующей схеме. Пусть 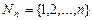, тогда подстановка обозначается как 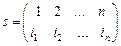, где ,

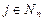
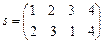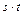Пусть , . Произведением называется подстановка, получаемая по правилу: умножение начинаем с подстановки t: 1 переходит в 2, далее находим в подстановке s число 2, которое переходит в 3 и т.д. Окончательно получим .

Выполнение аксиомы 1 следует из цепочки равенств для любого a

,

,

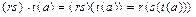то есть

.

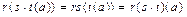В аксиоме 2 в качестве нейтрального элемента используется тождественная подстановка , то есть , в которой каждый элемент переходит в себя (порядок чисел в верхней строке не важен).

Для аксиомы 3 в качестве обратного элемента рассматривается подстановка 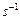, действующая наоборот, то есть 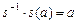или 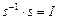. Для подстановки s обратная

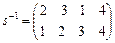. В самом деле, .

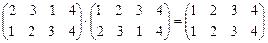Тем самым показано, что конечные подстановки образуют группу по умножению. В дальнейшем они будут использованы при аксиоматическом построении и вычислении определителей.

Относительно группы с операцией сложения заметим, что обычно она абелева и используются аксиомы 1) – 4) с соответствующей поправкой на знак операции.

Примерами таких групп являются множества целых чисел 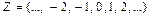, множество четных целых чисел.

Множество H называется подгруппой группы G.

Пример I.2. Показать, что множество нечетных целых чисел не является группой.

Покажем, что для любых элементов a, b группы G, уравнения 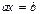и 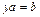имеют единственное решение: 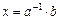и 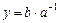. В самом деле, имеем

,

.

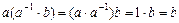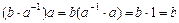Аналогично можно доказать обратимость сложения – это вычитание, для групповой операции сложения: .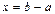

Кольцо

Пусть задано непустое множество K с двумя алгебраическими операциями: сложения и умножения [2]. Множество K называется кольцом, если выполняются свойства (аксиомы)

A. Сложение:

1) ;

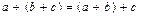2) ;

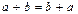3) существует решение уравнения

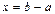, (обратимость сложения).

B. Умножение:

4) .

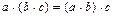C. Дистрибутивность умножения относительно сложения:

5) ;

6) .

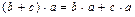Из аксиом набора A, B, C (1–6) следует, что кольцо образует абелеву группу относительно сложения. В такой группе 0 является «поглощающим» элементом, то есть 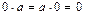. Единицей кольца является символ 1, причем .

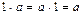Кольцо не обязано обладать единицей, а также не всегда , если и [3, 11].

Если в B добавлена аксиома , то кольцо называется коммутативным.

Кольцо одно из самых популярных универсальных алгебр. Примеры кольца: множество Z целых чисел; множество Q рациональных чисел; множество R вещественных чисел; множество C комплексных чисел; множество многочленов от одного или нескольких переменных; множество квадратных матриц; множество векторов 3-х мерного пространства с операциями сложения и векторного произведения и др.

Подведем некоторые итоги. Алгебра, как часть математики, в своем развитии прошла два неравноценных по времени этапа. Первый этап тысячелетний, до середины XIX в. Алгебру этого времени условно назовем элементарной. Были решены все поставленные перед ней до XVII в задачи. К этому времени алгебра не только получила самостоятельное развитие и уже не опиралась на геометрию, но ее методы стали использоваться и в самой геометрии. Завершился первый этап созданием общей теории решения систем линейных алгебраических уравнений, комплексных чисел и решением проблемы разрешимости алгебраических уравнений в радикалах.

Второй этап (последние 150 лет) условно назовем современной алгеброй. Отметим её вклад в теорию множеств, создание универсальных алгебр и алгебраических систем – глубоко разработанной теории, объединяющей алгебру и математическую логику.

На долю линейной алгебры отнесем изучение линейных (векторных) пространств, линейных преобразований (операторов, функций) билинейных и квадратичных форм на линейных пространствах и, кроме того, исследование решений систем линейных уравнений и неравенств. Ясно, что основным инструментом исследования являются теория множеств, математическая логика и методы, собственно, самой алгебры, не говоря об арифметике [3, 7].

Результаты, полученные в линейной алгебре, востребованы в математических и естественных науках, математической экономике, из прикладных отметим компьютерные науки: параллельное программирование, теорию вычислительных систем и суперкомпьютеров. Последнее связано с тем, что для повышения эффективности работы программного обеспечения высокопроизводительных вычислительных средств должен быть обеспечен массовый параллелизм, подобно человеческому мозгу, состоящему » из 10¹² нейронов, внутренняя логика которого обладает практически предельными возможностями для параллелизма. Существует направление в науке – теория нейронных систем [12] и сетей с компонентами из искусственных нейронов. Методы линейной алгебры в них являются основными при проверке эффективности работы параллельных программ.

Множества

Множество – фундаментальное понятие математики, используемое почти во всех ее разделах. Каждый, имеющий отношение к науке, будь то математик, инженер или философ, в своих исследованиях всегда приходит к обобщениям, т.е. рассматривает некоторую совокупность объектов как целое. Известное определение одного из основателей теории множеств Г. Кантора: «Под множеством понимается объединение в одно общее объектов, хорошо различаемых нашей интуицией или мыслью», – первоначально не вызвало возражений. Со временем, когда идеи Кантора стали проникать в умы исследователей, появились противоречия (антиномии) и определение Кантора перешло в разряд поясняющих понятий. Иначе и быть не могло, поскольку множество есть понятие исходное, на котором конструируются остальные понятия современной математики и, следовательно, пока неопределяемое.

Будем придерживаться мнения, что множество – совокупность объектов, объединенных общим признаком, свойством. Объекты множества называются его элементами. Описание элементов есть описание множества и наоборот. Если число элементов множества ограничено, то оно называется конечным, иначе – бесконечным. Если число элементов множества мало, то его описание обычно трудностей не вызывает (достаточно перечислить его элементы). Если число элементов велико или бесконечно, то указывают характеристическое свойство, связывающее элементы множества, например, 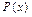читается «любой элемент x множества обладает свойством P ». (Ранее, при обсуждении понятия универсальной алгебры, характеристическим свойством множеств объявлялась алгебраическая операция или система ее аксиом). Свойство P не должно быть противоречивым или слишком длинным (чтобы мысль не терялась). По этой причине считается неэтичным употреблять выражение «множество всех множеств», поскольку оно еще не построено, к тому же это дополнительный источник антиномий, которых в теории множеств накопилось немало [10]. В связи со сказанным основания теории множеств будем излагать, используя аксиоматический подход. Конечно, аксиомы тоже основаны на интуитивном представлении о множествах, но благодаря такому подходу не будет возникать необходимости привлекать интуитивное представление при выявлении тех или иных свойств множеств, следующих из систем аксиом.

При изучении свойств множеств часто возникает необходимость группировать элементы множеств по признакам. Если все элементы множества распределены по группам и нет элемента, который мог бы находиться в двух группах, то множество разбито на непересекающиеся группы или классы.

Оказывается, что не всегда множество можно разбить на классы, хотя способов достаточно много. Пусть мы пожелали получить на некотором числовом множестве разбиение чисел по признаку: любые два числа a, b принадлежат одному классу, когда 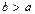. Такого разбиения быть не может [3], ведь по условию никакое число не может попасть в один класс с самим собой, поскольку получается, что должно быть 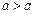, а это невозможно (сравни с ). Поэтому для того, чтобы разбиение на классы было осуществимо, должны быть выработаны условия осуществимости. В алгебре этому посвящен раздел, изучающий отношения – одна из форм взаимосвязи объектов исследования. Под отношениями понимаются, например: «…больше чем…», «…следует…», отношение порядка, эквивалентности, функциональное отношение, однозначное и взаимнооднозначное соответствие и др.

Пусть задан признак: «элемент a связан с элементом b отношением эквивалентности», тогда будем говорить, что a эквивалентно b и писать: a ~ b.

Определение. Отношением эквивалентности для элементов a, b, c, … множества, называется признак, удовлетворяющий условиям:

1) рефлексивности, т.е. a ~ a;

2) симметричности, т.е. если a ~ b, то b ~ a;

3) транзитивности, т.е. если a ~ b и b ~ c, то a ~ c.

Понятия, родственные эквивалентности, – равенство, тождество. Легко проверить выполнение этих условий для классов.

Строение множеств

Исходными символами в теории множеств являются

а) знаки: «=» – равенство, «Î» – принадлежность, «Ì» – включение;

б) вспомогательные знаки: «}», «{» – правая и левая фигурные скобки служат для выделения описания множеств, «)», «(» – скобки для однозначного восприятия построенных формул; разделительные знаки: «®» – читается «следует» и «,» – запятая;

в) буквы, число которых бесконечно (не путать с описанием множеств), возможны индексы для обозначения множеств: A, B, C, …, , , , …, для обозначения элементов множеств: a, b, c, …, , , , ….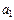

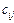г) логические знаки: «&» – читается «и», «Ú» – читается «или»;

д) кванторы (лат. quantor – сколько) – количественная характеристика внутренней связи множества и его элементов – общности «"» – читается «для всех» – и существования «$» – читается «существует».

Принадлежность элемента a множеству A записывается «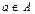 », читается «элемент a принадлежит множеству A », а принадлежность множества B множеству A записывается « 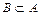», читается «множество B включено во множество A ». Если каждый элемент множества A является элементом множества B, и обратно, то пишут « 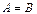», то есть множества совпадают (изоморфны). Если каждый элемент множества B находится в A и в A есть хотя бы один элемент, не принадлежащий B, то B есть собственное подмножество A, пишут « 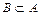», если таких элементов может не быть, то – « ».

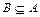Если множество A состоит из элементов a, b, c, то есть конечное, то пишут 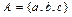. Если множество A бесконечное, то пишут 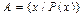, читается «множество элементов x обладает свойством P ». Например, запись 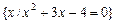описывает множество действительных корней уравнения 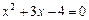; очевидно, это множество состоит из двух элементов {-4, 1}.

Пусть , где R – множество действительных чисел. Это множество может быть интерпретировано и как множество, состоящее из трех элементов, являющихся корнями уравнения, и как множество, у которого хотя бы один из них есть действительное число, в то время как два других корня могут быть комплексными числами.

Поскольку при таком описании мы не можем точно сказать, является ли произвольно выбранное число элементом множества, то это означает, что его характеристическое свойство неопределенно. Следует данное множество определить, например, так: дано множество, состоящее из одного элемента, являющегося единственным действительным корнем уравнения 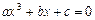. Заметим, что условие не является необходимым.

Может оказаться, что во множестве, заданном характеристическим свойством, не содержится ни одного элемента. Такое множество называется пустым и обозначается символом «Æ». Например, 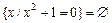, если решение уравнения рассматривать в области действительных чисел, и состоит из двух элементов 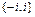, если решать уравнение в области комплексных чисел, где 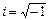. Таким образом, пустое множество Æ можно определить как множество, не имеющее ни одного элемента.

Кстати, уже можно сформулировать аксиому: «существует хотя бы одно множество». Кажется, что пустое множество не несет никакой конструктивной информации. На самом деле это не так. Его введение позволило получить, например, фундаментальные результаты как в самой алгебре, так и в других теориях, например теории вероятностей [8, 12].

Пусть M – множество и множество 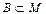, говорят, что B подмножество M. Пустое множество является подмножеством любого множества, т.е. .

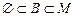Множество, элементами которого являются другие множества, называется системой множеств.

Из любого множества можно построить систему множеств, например:

а) дано Æ, тогда 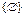есть система множеств, состоящая из одного элемента Æ, а 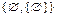– множество, состоящее из двух элементов: Æ и 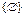, т.е. пустое множество и множество, состоящее из одного элемента – пустое множество, и т.д.;

б) дано множество M, тогда 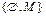– система множеств, состоящая из двух элементов Æ и M;

в) дано множество 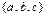, состоящее из трех элементов. Все его возможные подмножества: Æ, 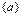, , 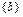, , 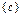, , 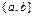, 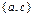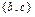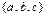число которых равно .

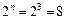Обозначим через 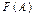систему множеств, состоящую из всех подмножеств множества A. Говорят, что 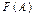порождена множеством A.

Множества типа 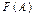относятся к классу универсальных. В теориях и приложениях важными являются бесконечные универсальные множества (пространства). В таких множествах можно выполнять действия с целью получения других множеств. Выполнения этих действий в универсальных множествах, аналогичных алгебраическим операциям в универсальных алгебрах, приводит к результату, который определяется как подмножество исходного множества. Эти операции называются теоретико-множественными.

К ним относятся операции: объединение «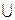 », пересечение « », разность «-», в универсальных множествах рассматривается операция дополнение (отрицание) «Ø».

Эти операции сильно напоминают алгебраические, что находит подтверждение и в аксиомах теории множеств [6], основанных, в общем-то, на здравом смысле.

1. Аксиома объемности. Если множества A и B составлены из одних и тех же элементов, то они равны, т.е.

~ ® .

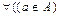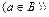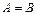2. Аксиома суммы. Для произвольных множеств A и B существует множество (сумма A и B), элементами которого являются все элементы множества A и все элементы множества B, и никаких других элементов не содержит, т.е.
"()~().

3. Аксиома умножения. Для произвольных множеств A и B существует множество 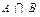(произведение множеств A и B), состоящее из тех и только тех элементов, которые содержатся и в A, и в B, т.е. "()~().

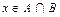4. Аксиома разности. Для произвольных множеств A и B существует множество (разность множеств A и B), элементами которого являются те и только те элементы A, которые не содержатся в B, т.е. "(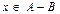)~Ø()~ .

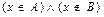5. Аксиома существования. Существует по крайней мере одно множество.

Данная система аксиом непротиворечива и неполна.

Аксиомы не являются независимыми. Например, аксиома умножения выводится из аксиомы разности, так как .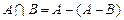

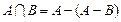Из аксиом 1 и 2 следует единственность 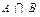, аналогично получаем единственность .

Из аксиом 1, 4 и 5 следует, что существует единственное множество – не содержащее элементов, т.е. пустое множество.

Отношение включения «Ì», можно определить формулой ()~().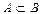

Аксиомы 1–5 позволяют получать новые множества, изучать их свойства и т.д.

Алгебра множеств

Пусть F – система множеств. Если для любых 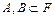выполняется операции

1) ,

2) ,

3) Ø ,

то говорят, что в F задана алгебра множеств, а если выполняется операция

4) , ,

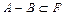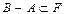то говорят, что в F задано поле множеств.

Аксиомы не являются независимыми, поскольку, например, =Ø .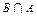

Применяя алгебраическую терминологию, можно сказать, что алгебра множеств есть коммутативное кольцо с единицей.

В теории вероятностей алгебра множеств составляет часть ее аксиоматического построения [8].

Число

Развитие

Число – одно из основных понятий математики. Число выражает результат измерения или счета. Для изображения чисел используют различные специальные знаки, называемые цифрами. В Древней Руси, культура которой была тесно связана с греческой, числа, как и у греков, записывались буквами. Поступали просто: над буквой ставили специальный знак «~», называемый титло. Числа 1,2,3… обозначались буквами 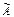, , 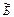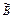…. Большие числа записывались также буквами, но впереди ставили знак «¹», например, 1000 записывалась как ¹ 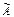, 3000 – ¹ 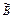, а число 10000 как , – и называлось оно «тьма» (отсюда выражение «тьма народу»). Число 100000 называлось легион, известно обозначение числа 10⁴⁹, которое называлось «колода».

В России уже в XVII в. во всех математических рукописях встречается только позиционная (упорядоченная) десятичная система счисления, которая состоит из десяти цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Впервые появилась в Индии и через арабов попала в Россию, отсюда и название – арабские цифры. Из этих цифр можно построить любое, сколь угодно большое, но конечное натуральное число.

Постепенно складывалось представление о бесконечности натуральных чисел.

Наряду с натуральными числами применялись дроби – числа, составленные из целого числа долей единицы. Множества натуральных чисел и дробей было достаточно, чтобы выразить результат любого измерения. Долгое время считалось, что измерения всегда выражаются либо целыми натуральными числами, либо их отношениями (число 0 – «нуль»), еще не было известно, но и после его появления во множество натуральных чисел он так и не попал из-за конструктивных причин построения чисел).

Древнегреческие ученые могли выполнять все арифметические действия, включая возведения в степень, извлечение корня, имели понятие об аналоге нуля, но этого было недостаточно, чтобы все операции объединить в единую систему, поскольку не существовало еще идеи числа. Поэтому сильнейшим шоком для всех оказалось открытие несоизмеримости диагонали квадрата с его стороной. Оказалось, что натуральных чисел вместе с дробями недостаточно, чтобы решить эту проблему, когда выяснилось, что диагональ квадрата со стороной 1 равна 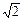. Такие числа они назвали иррациональными, то есть недоступными разуму.

Возможно, что отсюда началась эпоха теоретической математики: поскольку иррациональные числа в десятичной системе счисления представимы бесконечной непериодической дробью, то из опыта никакими измерениями их получить никогда не будет возможным.

Математика разделилась на две части: арифметику – науку о числах и геометрию – науку об объектах, их формах и величинах: длине, площади, объеме.

С развитием алгебры, то есть с появлением уравнений, для их решения, уже в первой степени, потребовались отрицательные числа и 0.

Числа, целые и дробные (положительные и отрицательные) и 0, стали называть рациональными.

Изучение понятия числа осуществлялось не только путем обобщения (были сначала открыты комплексные числа, а затем осуществлено формальное построение теории действительных чисел), но и путем выделения важных частных случаев. Во множестве действительных чисел выделены множества рациональных и иррациональных чисел. Рациональные числа всегда представимы в виде десятичных дробей, в которых, начиная с некоторого места, числа повторяются (имеют период), а иррациональные периода не имеют, то есть их задают бесконечной десятичной непериодической дробью.

В XIV в., в связи с изучением кубических уравнений, в процессе вывода формулы для вычисления их корней (решений) появлялись арифметические корни из отрицательного числа, хотя конечная формула их не содержала, давая действительный корень уравнения.