В.А. Павский
ЛИНЕЙНАЯ АЛГЕБРА
Учебное пособие
Для студентов вузов
Кемерово 2013
УДК 512.64(075)
ББК 22.143я7
П12
Рецензенты:
Н.Н. Данилов, д-р физ.-мат. наук, профессор; заведующий
кафедрой математической кибернетики КемГУ;
А.М. Гудов канд. физ.-мат. наук, доценткафедры UNESCO
по новым информационным технологиям КемГУ
Рекомендовано редакционно-издательским советом
Кемеровского технологического института
пищевой промышленности
Павский, В.А.
П12 Линейная алгебра: учеб. пособие / В.А. Павский; Кемеровский технологический институт пищевой промышленности. – Кемерово, 2013. – 188 с.
ISBN 978-5-89289-761-7
Учебное пособие составлено в соответствии с программой дисциплины «Линейная алгебра» и предназначено для студентов всех форм обучения. Будет полезно аспирантам и преподавателям
УДК 512.64(075)
ББК 22.143я7
ISBN 978-5-89289-761-7
|
© КемТИПП, 2013
Оглавление
Основные обозначения. 6
ВВЕДЕНИЕ. 8
I. Введение в линейную алгебру. 10
§ 1. История развития алгебры.. 10
Группа. 14
Кольцо. 16
§ 2. Множества. 18
§ 3. Строение множеств. 20
Алгебра множеств. 24
§ 4. Число. 24
Развитие. 24
§ 5. Числовые множества. 27
Бесконечные множества. 28
Натуральный ряд. 29
Множество целых чисел. 31
Множество рациональных чисел. 31
Множество действительных чисел. 34
Множество комплексных чисел. 36
Суммы и произведения. 41
Приближенные вычисления. 42
II. Элементы линейной алгебры.. 43
§ 1. Матрицы и определители. 43
Определитель матрицы.. 47
Аксиоматическое построение теории определителей. 51
Обратная матрица. 54
Ранг матрицы.. 56
§ 2. Системы линейных алгебраических уравнений. 57
Методы решения СЛАУ.. 58
Однородная система линейных алгебраических уравнений (ОСЛАУ) 64
§ 3. Системы линейных алгебраических неравенств. 66
III. Линейные пространства. 69
§ 1. Линейная зависимость. 75
§ 2. Линейные комбинации. Базисы.. 77
§ 3. Подпространства. 84
§ 4. Прямые суммы.. 85
§ 5. Евклидовы пространства. 88
§ 6. Координатные системы.. 92
IV. Векторная алгебра. 95
§ 1. Векторы.. 95
§ 2. Линейные операции над векторами. 96
§ 3. Проекция вектора на ось. 98
Координаты вектора. 101
Деление отрезка в данном отношении. 103
§ 4. Базис системы векторов. 104
§ 5. Скалярное произведение векторов. 107
§ 6. Векторное произведение векторов. 111
§ 7. Смешанное произведение векторов. 113
V. Аналитическая геометрия. 115
§ 1. Системы координат на плоскости. 115
§ 2. Уравнение линии на плоскости. 119
§ 3. Уравнение поверхности и линии в пространстве. 120
§ 4. Прямая и плоскость в линейном пространстве. 122
Уравнение плоскости, проходящей через три точки. 125
Взаимное расположение плоскостей. 129
Уравнение прямой в пространстве R 3 130
Уравнение прямой, проходящей через две точки. 132
Прямая как линия пересечения плоскостей. 133
Расстояние от точки до прямой. 136
Угол между прямой и плоскостью.. 141
Угол между плоскостями. 142
VI. Линейные операторы.. 144
§ 1. Линейный оператор. 144
Векторные свойства линейных операторов. 146
Умножение операторов. 147
Матрицы операторов. 149
Изменение базиса. 153
Подобие. 154
§ 2. Характеристический многочлен. 156
VII. Билинейные и квадратичные формы.. 160
§ 1. Билинейные формы.. 160
§ 2. Квадратичные формы.. 162
Приведение к каноническому виду. 163
VIII. Гиперповерхности и поверхности второго порядка. 170
Классификация линий второго порядка. 171
Окружность. 172
Эллипс. 173
Гипербола. 175
Парабола. 176
Классификация поверхностей второго порядка. 178
ЗАКЛЮЧЕНИЕ. 186
СПИСОК ЛИТЕРАТУРЫ.. 187
Основные обозначения
| символ | значение |
A, B, …, 
| обозначения множеств |
| a ~ b | отношение эквивалентности |
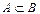
| логический знак принадлежности множества множеству |

| логический знак принадлежности элемента множеству |
 , ,

| знак равенства и равенства по определению |
| Ù, & | «и», логический знак конъюнкция |
| Ú | «или», логический знак дизъюнкция |
| " | «для всех» «любой», квантор всеобщности |
| $ | «существует», квантор существования |
| Ç | знак пересечения множеств |
| È | знак объединения множеств |
 , , 
| отрицание A |

| знак дополнения множеств |
| ▼ | знак окончания доказательсва |
| N | множества натуральных чисел |
| Z | множества целых чисел |
| Q | множества рациональных чисел |
| R | множества действительных чисел |
| C | множества комплексных чисел |
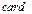
| символ кардинального числа |
æ0= 
| «алеф-нуль», мощность N |
2æ0= 
| мощность R |
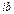
| мнимое число, 
|

| комплексное число, 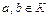
|
| i | мнимая единица, 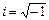
|
| å | знак обозначения сокращенного суммирования |
| Õ | знак обозначения сокращенного умножения |
| A, B, … | оператор |
A, 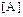 , ,  , , 
| матрица |
| символ | значение |
AT, 
| транспонированная матрица |
| E | единичная матрица |
| A -1 | обратная матрица |
| D, det A, | A | | определитель матрицы |
| n! | «эн-факториал», произведение  , , 
|

| характеристический многочлен |

| символ числа сочетаний из n элементов по k,
а 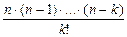 - число вариантов - число вариантов
|
| r, rangA | ранг матрицы A |

| единичный вектор |
 , ,  , , 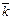
| единичные координатные векторы |
| L, Ln | линейное пространство |
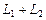
| прямая сумма |
 , , 
| скалярное произведение пары векторов |

| векторное произведение векторов |
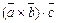 , , 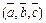
| смешанное произведение векторов |

| проекция вектора  в направлении вектора в направлении вектора 
|
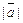
| длина вектора 
|
ВВЕДЕНИЕ
Особенностью развития современного общества является применение математических моделей, методов и быстродействующих вычислительных средств в различных областях знаний. Создание любого нового продукта практически всегда сопровождается применением математических методов и математического (в частности имитационного) моделирования. Ведущая роль среди фундаментальных математических наук отведена алгебре, которая, совместно с математической логикой, пытается формализовать всю математику с целью создания единой математической теории с дальнейшим внедрением ее в программное обеспечение искусственного интеллекта.
Современная линейная алгебра, являясь разделом алгебры, широко применяется в различных областях науки и приложениях. Её модели и методы составляют наиболее разработанную часть программного обеспечения в плане параллельного программирования, а алгебраические структуры являются частью математического аппарата, используемого при проектировании и создании суперкомпьютеров и других средств быстродействующей вычислительной техники. В сущности, теория множеств, алгебра, математическая логика уже составляют язык современной математики и многих ее приложений.
Предварительная информация о дисциплине «Линейная алгебра» в пособии представлена в объеме несколько большем, чем необходимо. Это обосновывается тем, что в последующих математических дисциплинах, изучаемых в вузе, эта информация будет полностью востребована.
Алгебра или универсальная алгебра – часть математики, изучающая алгебраические операции.
Линейнаяалгебра – раздел алгебры, изучающий линейные пространства, линейные операторы (преобразования) и смежные вопросы.
Содержательный смысл определений скрыт в их концентрированности и станет более доступным после ознакомления с этапами развития алгебры, её методами, как фундаментальной науки.
Пособие состоит из введения, восьми разделов, списка литературы, заключения.
Приведен список основных обозначений. Оглавление достаточно подробно и может быть использовано в качестве именного указателя. Особое внимание при изучении линейной алгебры следует уделить ссылкам на литературу, которая, несомненно, поможет лучше усвоить наиболее трудновоспринимаемые разделы и понять ее фундаментальное значение для математики и науки.
Выражаю искреннюю благодарность доктору наук Ивановой С.А., взявшей на себя тяжелый труд по оформлению пособия. Ее критические замечания помогли не только улучшить качество изложения, но и сделать доступным содержащийся в пособии материал.
I. Введение в линейную алгебру