Ранее отмечалось, что многие множества, существенно различаясь по природе своих элементов, имеют одинаковые свойства, то есть могут быть описаны, с точки зрения современной алгебры, единой системой аксиом. Наиболее востребован практикой оказался класс множеств, обладающих свойствами линейного пространства. Часто их называют векторными, поскольку векторные величины получили широкое распространение в различных научно-практических исследованиях и приложениях. Кроме того, векторные пространства геометрически наглядны, что делает линейные пространства понятными, расширяя тем самым область использования их в науке и практических исследованиях.
Во введении понятие числового поля определялось аксиоматически. Рассмотрены поля рациональных чисел Q, действительных чисел R и комплексных чисел C. В этом разделе введем аксиоматически линейные пространства.
Пусть дано любое числовое поле и все скаляры являются его элементами [11].
Определение. Линейным пространством над числовым полем, например R, называется множество L элементов, удовлетворяющее аксиомам:
A) Для любой пары 
, 
элементов из L всегда найдется элемент 
, называемый суммой элементов и , что выполняется
1) 
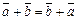(коммутативность);
2) 
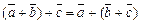(ассоциативность);
3) существует нейтральный элемент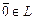 
, называемый начальным, такой, что 
;
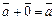4) каждому элементу соответствует однозначно определенный элемент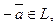 
такой, что 
.
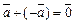B) Для любой пары из a, b и , 
, 
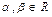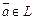найдется элемент 
, 
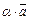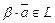, называемый произведением a и или b и соответственно, такой, что
5) 
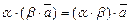(ассоциативность умножения на скаляры);
6) 
.
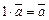7) 
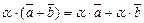– умножение на скаляры дис-трибутивно (сочетательно) относительно сложения;
8) 
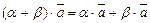– умножение на элементы дис-трибутивно относительно сложения скаляров.
|
|
Отношения между линейным пространством L и полем скаляров выражают словами: линейное пространство L над полем скаляров.
В дальнейшем под полем скаляров будем понимать основное поле R действительных чисел, а имея дело с линейными пространствами в обозначениях и геометрической интерпретации, будем использовать векторные обозначения, что и было сделано в аксиомах.
Вектор (лат. vector – скользящий) – в геометрическом пространстве определяется как отрезок прямой, имеющий направление; задается упорядоченно: начало вектора (точка A) и конец (точка B). Для обозначения такого вектора используются а) пара букв 
или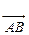 
, а также одна буква 
или a (полужирный шрифт), б) на рисунках как направленный отрезок прямой. Таким образом, векторные обозначения и геометрические векторы – суть обозначения элементов линейного пространства.
Рассматривают геометрические векторные пространства трех видов векторов: связанные, скользящие и свободные. В пространстве свободных векторов достаточно иметь одинаковые направления; скользящие векторы лежат на одной прямой; связанные векторы имеют общее начало. Длина для всех видов векторов определяется его модулем -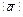 
. Из условия упорядоченности обозначений вектор 
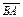противоположен вектору . Вектор, у которого начало совпадает с концом, например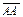 
, называется нуль-вектором, 
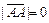, то есть обозначение совпадает с числом 0; ему приписывают любое направление. Вектор 
, длина которого 
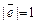, называется единичным, помимо этого свойства, он выполняет функции масштаба.
Векторы называются коллинеарными, если они лежат в одной или в параллельных прямых, и компланарными, если лежат в одной или параллельных плоскостях.
|
|
Зададим вектор (свободный) аксиоматически. Определим векторное пространство как понятие, обобщающее понятие совокупности всех векторов обычного трехмерного пространства. Элементы числового поля будем называть по-прежнему скалярами.
Определение. Векторным пространством над скалярным полем P называется множество L векторов, в котором определена операция сложения векторов и операция умножения векторов на скаляры из основного поля P, задаваемых аксиомами:
A. Сложение.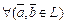 
, 
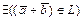, называемый суммой векторов и , что
1) ;
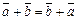2) ;
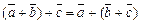3) существует нулевой вектор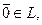 
такой, что ;
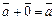4) для вектора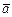 
найдется единственный противоположный вектор 
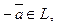такой, что ;
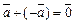B. Умножение.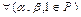 
, 
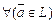Þ $ вектор 
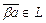, называемый произведением скаляра b и вектора 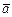, что
5) ;
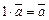6) 
;
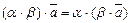C. Умножение дистрибутивно относительно
7) сложения векторов, ;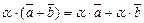
8) сложения скаляров, .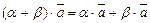
Из аксиом вытекают важные свойства векторов L ():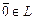
1) 
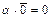; то есть умножение нуль–вектора на скаляр дает число 0;
2) 
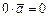; умножение числа 0 на вектор дает также число 0;
3) 
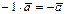, то есть чтобы получить вектор, противоположный заданному, достаточно умножить его на -1.
Аксиомы 1) – 4) образуют абелеву группу, а аксиомы
5) – 8) отражают тот факт, что умножение элементов на скаляры является линейной функцией (оператором, преобразованием) элементов из L. Это подтверждает не только внешнее сходство аксиом поля и векторного пространства, но и их внутреннюю связь, другими словами, понятия линейное пространство и векторное пространство – изоморфны.
|
|
Пример III.1. Рассмотрим множество векторов на плоскости. Покажем, что оно образует линейное пространство L 2 над полем чисел R. Достаточно проверить выполнение аксиом 1) – 8). Проверку осуществим, используя геометрические образы. Исходя из определения свободных векторов , , совместим параллельным переносом конец вектора с началом вектора , а затем – начало вектора с концом вектора . Полученный вектор 
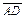назовем суммой векторов и (рис. III.1), то есть 
.
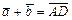Положим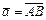 
, тогда 
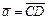, аналогично 
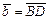, тогда 
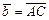(рис. III.1).
А. Сложение. Если векторы неколлинеарные, то по «правилу треугольников» сложения векторов, имеем
1) 
.
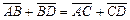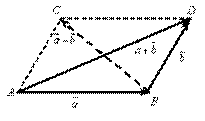
Рис. III.1
Для коллинеарных векторов это очевидно, так как D ADB вырождается в отрезок прямой.
2) 
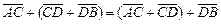или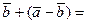 
.
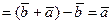Тот факт, что векторы параллелограмма попарно равны, не является принципиальным. Для общего случая, можно рассмотреть любой четырехугольник на плоскости.
3) Очевидно, если обозначить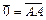 
;
4) Следует из доказательства аксиомы 2.
B. Умножение. Пусть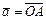 
лежит на прямой (рис. III.2).
5) 
;
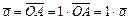Рис. III.2
6) положим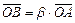 
, а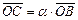 
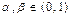(рис.2), тогда 
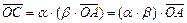или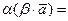 
.
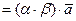C. Дистрибутивность.
7) Следует из свойств пропорциональности отрезков
(рис. III.3). В самом деле,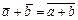 
. Пусть 
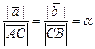, тогда
, 
, 
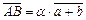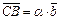Þ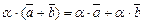 
.
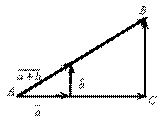
Рис. III.3
8) Следует из рис. III.2 и правил сложения векторов, если положить ,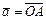 
, 
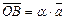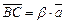, тогда 
.
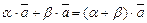Тем самым выполнение аксиом показано геометрически.
Пример III.2. Пусть R 2 множество всех упорядоченных пар действительных чисел и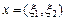 
, 
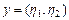, где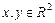 
. Положим по определению
1) 
;
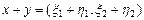2) 
;
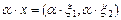3) 
;
4) 
,
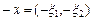где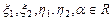 
.
Аксиомы групп A, B, C, очевидно, выполняются, следовательно, R 2 – двумерное действительное линейное пространство, в котором задана система координат.
Пример III.3. Если в примере 2 вместо пар рассматривать действительные числа, то множество R есть линейное пространство над самим собой, геометрически это числовая ось.
То же самое справедливо для любого другого скалярного поля.
Пример III.4. Пусть P – множество полиномов (многочленов) переменной x с действительными коэффициентами. Под сложением полиномов будем понимать обычное их сложение по правилу приведения подобных членов, а умножение на скаляр – обычное умножение полинома на действительное число. Нейтральный элемент – полином, все коэффициенты которого равны 0. Множество полиномов с действительными коэффициентами будет действительным линейным пространством.
Пример III.5. Определим на множестве действительных чисел R сложение действительных чисел и их умножение на скаляр являющегося рациональным числом, тогда множество R будет рациональным действительным линейным пространством.
Линейная зависимость
Перейдем к описанию свойств линейных пространств.
В первую очередь к ним относятся отношения между его
элементами.
Линейной комбинацией элементов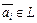 
над полем действительных чисел R называется элемент
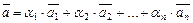, (III.1)
где ,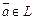 
, 
.
Определение. Множество элементов 
, называется линейно независимым, если из равенства
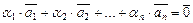, (III.2)
с необходимостью следует, что 
, 
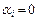. Ясно, что любая часть элементов из также линейно независимая. Если хотя бы одно из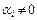 
, , то множество называется линейно зависимым.
Пример III.6. Пусть дано векторное множество . Если один из векторов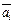 
, например, 
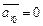, то такая система векторов линейно зависима. В самом деле, пусть множество 
, 
, …, 
, 
, …, 
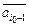линейно независимо, тогда из равенства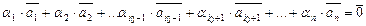 
следует, что 
.
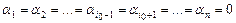Добавляя к этому множеству 
вектор, умноженный на 
, по-прежнему имеем равенство
.
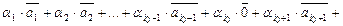
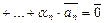Следовательно, множество векторов, как, впрочем, и любых других элементов, содержащих нулевой элемент, всегда линейно зависимо ▼.
Замечание. Если множество векторов пусто, то оно линейно независимо. В самом деле, если нет никаких индексов, то невозможно выбрать им соответствующие не равные нулю числа, чтобы сумма вида (III.2) была равна 0. Такая интерпретация линейной независимости может быть принята за доказательство, тем более что такой результат хорошо согласуется с теорией [11].
В связи со сказанным определение линейной независимости можно сформулировать так: множество элементов линейно независимо, если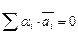 
и нет ни одного индекса, для которого 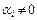. В частности, это множество может быть и пустым.
Пример III.7. Любые два скользящих вектора линейно зависимы. Напомним, что скользящими векторами называются векторы, лежащие на одной прямой. Взяв единичный вектор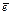 
, можно получить любой другой вектор умножением на соответствующее действительное число 
, то есть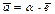 
или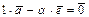 
. Следовательно, уже любые два вектора в одномерном пространстве линейно зависимы.
Пример III.8. Рассмотрим пространство полиномов, где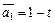 
, 
, 
, 
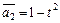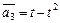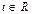. Запишем
.
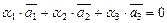Полагая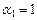 
, 
, 
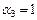, получим, тождественно по t
,
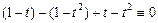то есть множество 
линейно зависимо. Заметим, что любое конечное множество вида 
, 
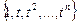линейно независимо. Для доказательства рассмотрим случай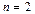 
, тогда из равенства
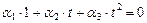, (III.3)
в случае предположения о его линейной зависимости, следовало бы, что существуют не все равные нулю числа a 1, a 2, a 3, что тождественно для любого выполняется (III.3), но это противоречит основной теореме алгебры: любой многочлен n -ой степени имеет не более чем n действительных корней. В нашем случае это уравнение имеет только два корня, а не бесконечное их множество. Получили противоречие.