Пусть 
. Будем говорить, что 
есть линейная комбинация элементов 
.
Теорема III.1 (основная). Множество ненулевых элементов 
линейно зависимо тогда и только тогда, когда некоторый элемент 
, 
является линейной комбинацией предшествующих элементов.
Доказательство. Необходимость. Предположим, что элементы 
, 
, …, 
линейно зависимы и пусть первое натуральное число, для которого элементы , , …, 
линейно зависимы, тогда
,
при не всех равных нулю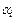 
и обязательно 
(иначе этим коэффициентом было бы 
, что противоречило бы заявленному). Отсюда имеем линейную комбинацию
.
Достаточность очевидна, поскольку, каждое множество, содержащее линейно зависимое множество, само линейно зависимо ▼.
Определение. Базисом (координатной системой) линейного пространства L называется множество A линейно независимых элементов, такое, что каждый элемент из L является линейной комбинацией элементов из A, 
[11].
Мы будем рассматривать конечномерные линейные пространства 
, 
.
Пример III.9. Рассмотрим трехмерное векторное пространство 
. Возьмем единичные векторы 
, 
, 
. Они образуют базис при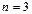 
.
Покажем, что векторы линейно независимы. В самом деле, имеем
или 
. Отсюда по правилам умножения вектора на число и сложения векторов (пример III.2) получим
или 
.
Следовательно, 
, 
, 
▼.
Пусть 
– произвольный вектор пространства , тогда исходя из аксиом линейного пространства получаем
.
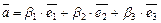Аналогичные рассуждения справедливы для пространства с базисом, 
. Из основной теоремы следует, что в произвольном конечномерном линейном пространстве L любой элемент 
может быть представлен как линейная комбинация его базисных элементов 
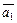, , …, , то есть
.
Причем такое разложение единственно. В самом деле, пусть имеем
,
тогда после вычитания получаем
.
Отсюда, в силу независимости элементов 
, 
,
, то есть 
▼.
Теорема III.2 (о дополнении до базиса). Пусть – конечномерное линейное пространство и 
– некоторое множество линейно независимых элементов. Если они не образуют базис, то в можно найти такие элементы 
, 
, …, 
, что множество элементов 
образуют базис в . То есть, каждое линейно независимое множество элементов линейного пространства может быть дополнено до базиса.
Доказательство. Поскольку пространство – конечномерное, то у него есть базис, состоящий, например, из n элементов, пусть это элементы 
. Рассмотрим множество элементов 
.
Применим основную теорему. В порядке следования элементов рассмотрим множество A. Оно заведомо линейно зависимое, поскольку любой из элементов 
есть линейная комбинация 
, 
, 
. Так как элементы , , …, 
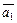– линейно независимые, то добавляя к нему последовательно элементы до тех пор, пока не появится первый элемент, например, 
, такой, что он будет линейной комбинацией предыдущих векторов этого множества, то есть 
. Выбрасывая этот элемент из множества A, получим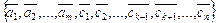 
. Продолжаем эту процедуру до тех пор, пока в этом множестве не останется n линейно независимых элементов, среди которых все элементы ,
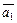, …, и n - m из элементов . Полученное множество и будет базисом ▼.
Пример III.10. Доказать, что векторы , , и 
образуют линейно зависимое множество, а любые три из них линейно независимы.
Покажем, что существуют не все равные нулю числа 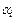, для которых
.
В самом деле, при 
, 
имеем
,
.
Линейная зависимость доказана. Покажем, что тройка векторов, например 
, 
, , образует базис. Составим равенство
,
.
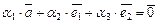Выполняя действия с векторами, получим
.
Приравнивая соответствующие координаты в правой и левой частях последнего равенства, получим систему уравнений 
, 
, 
, решая ее, получим 
.
Аналогичное рассуждение справедливо и для оставшихся троек векторов , 
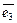, или , , .
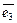Теорема III.3 (о размерности пространства). Все базисы конечномерного линейного пространства L состоят из одинакового числа базисных элементов.
Доказательство. Пусть даны два множества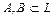 
, где 
; 
, 
. Каждому из них припишем одно из двух свойств, определяющих базис: 1) через элементы множества A линейно выражаются любые элементы из L, 2) элементы множества B представляют линейно независимую совокупность, но не обязательно всю из L. Будем считать, что элементы A и B упорядочены.
Рассмотрим множество A и применим к его элементам m раз метод из основной теоремы. Так как элементы из B линейно независимы, то получим, по-прежнему, линейно зависимое множество
. (III.4)
В самом деле, если бы 
, то получилось бы линейно независимое множество 
, а оставшиеся n элементов множества B линейно выражались бы через них, что невозможно, значит 
. Но этого тоже быть не может, так как по построению множество (III.4) обладает свойством базиса множества A. Поскольку пространство L конечномерное, то остается только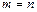 
, то есть два разных базиса пространства L состоят из одинакового числа элементов ▼.
Следствие. В любом n -мерном линейном пространстве
(
) можно найти бесконечно много базисов.
Доказательство следует из правила умножения элементов линейного (векторного) пространства на число.
Определение. Размерностью линейного пространства L называется число элементов, составляющих его базис.
Из определения следует, что пустое множество элементов – тривиальное линейное пространство – имеет размерность 0, что, как следует заметить, оправдывает терминологию линейной зависимости и позволяет заявить: n -мерное пространство имеет размерность n, 
.
Таким образом, подводя итоги сказанному, получаем, что каждое множество из n +1 элемента n -мерного линейного пространства линейно зависимо; множество из n элементов линейного пространства является базисом тогда и только тогда, когда оно линейно независимое (или каждый элемент пространства является линейной комбинацией элементов его базиса); в любом линейном пространстве число базисов бесконечно.