До сих пор мы изучали понятие линейности и не касались количественных характеристик: угла и длины, что особенно важно для приложений. Для лучшего понимания дальнейшего рассмотрим двумерное линейное пространство над полем действительных чисел, с введенной в нем декартовой прямоугольной системой координат [11].
Пусть  ,
,  . Тогда длина отрезка,
. Тогда длина отрезка,
соединяющего концы векторов  ,
,  , находится по очевидной формуле
, находится по очевидной формуле  . Для расстояния до
. Для расстояния до  от начала
от начала  введем обозначения
введем обозначения  . Перейдем к углам между векторами. Если j – угол между отрезком, соединяющим O с
. Перейдем к углам между векторами. Если j – угол между отрезком, соединяющим O с  и положительной осью Ox, а
и положительной осью Ox, а 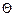 – угол между отрезком, соединяющим O с
– угол между отрезком, соединяющим O с 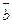 и той же осью, то углом между векторами
и той же осью, то углом между векторами  и
и 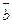 будет
будет  , тогда
, тогда
 .
.
Введем обозначение
 .
.
С помощью полученного выражения можно очень простыми формулами выразить углы между векторами их длины.
Рассмотрим скалярное произведение векторов  и
и  , имеем по определению
, имеем по определению
 , (IV.11)
, (IV.11)
где j – угол между векторами  и
и  .
.
Пусть  – проекция вектора
– проекция вектора  в направлении вектора
в направлении вектора  , тогда
, тогда  (рис. IV.7).
(рис. IV.7).

Рис. IV.7.
Отсюда  , следовательно,
, следовательно,  , аналогично получаем
, аналогично получаем
 , где
, где  .
.
Геометрические свойства скалярного произведения [4]
1) Необходимым и достаточным условием ортогональности двух ненулевых векторов является равенство 0 их скалярного произведения.
Замечание 1. Если хотя бы один из векторов равен нулю, то будем считать, что нулевой вектор ортогонален любому вектору.
Замечание 2. Под углом между векторами будем считать тот угол, который не превосходит p.
2) Два ненулевых вектора составляют острый (тупой) угол тогда и только тогда, когда их скалярное произведение положительно (отрицательно).
Алгебраические свойства скалярного произведения [4]
1)  (коммутативность);
(коммутативность);
2)  (ассоциативность);
(ассоциативность);
3) 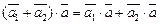 (дистрибутивность);
(дистрибутивность);
4)  , если
, если  нулевой, и
нулевой, и  в противном случае.
в противном случае.
Выразим скалярное произведение векторов через их координаты. Пусть  ,
,  , тогда получаем
, тогда получаем
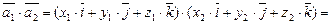
 ,
,
учитывая, что  ,
,  .
.
Определение. Если в Евклидовом пространстве задана декартовая система координат, то скалярное произведение векторов  и
и  называется число, заданное суммой произведений соответствующих координат, то есть
называется число, заданное суммой произведений соответствующих координат, то есть
 . (IV.12)
. (IV.12)
Из свойств скалярного произведения векторов и формулы (IV.12) следует необходимое и достаточное условие ортогональности векторов  и
и  :
:
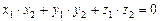 .
.
Из первого определения скалярного произведения векторов и формулы (IV.11) следует, что
 . (IV.13)
. (IV.13)
Пример IV.4. Найти такое число l, для которого векторы  и
и  ортогональны.
ортогональны.
Решение. Скалярное произведение ортогональных векторов равно нулю, поэтому 
 , получили линейное алгебраическое уравнение относительно l, отсюда
, получили линейное алгебраическое уравнение относительно l, отсюда  или
или  , то есть при
, то есть при  векторы
векторы  и
и 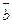 будут ортогональны. В самом деле, имеем
будут ортогональны. В самом деле, имеем  .
.
Пример IV.5. Найти углы и длины сторон треугольника с вершинами 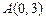 ,
, 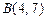 ,
,  .
.
Решение. Определим координаты векторов:  ,
,  ,
,  , так как угол A образован векторами
, так как угол A образован векторами  и
и  , то
, то
 .
.
По таблицам находим
 .
.
Аналогично,  , значит
, значит  – прямой. Поскольку сумма углов треугольника равна 180°, то
– прямой. Поскольку сумма углов треугольника равна 180°, то  . Длины сторон – это длины соответствующих векторов, поэтому:
. Длины сторон – это длины соответствующих векторов, поэтому:
 ;
;  ;
;  .
.
Пример IV.6. Найти скалярное произведение векторов  и
и  , если
, если  ,
, 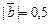 , а угол между векторами
, а угол между векторами  и
и 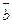 равен 60°.
равен 60°.
Решение. Имеем, последовательно:


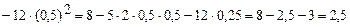 .
.
§ 6. Векторное произведение векторов [4]
Векторы называются упорядоченными, если указано место каждого из векторов. Упорядоченная тройка векторов  ,
,  ,
,  называется правой, если с конца вектора
называется правой, если с конца вектора  поворот на меньший угол от вектора
поворот на меньший угол от вектора  к вектору
к вектору  осуществляется против часовой стрелки.
осуществляется против часовой стрелки.
В дальнейшем будем рассматривать только правые тройки базисных векторов.
Определение. Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , удовлетворяющий условиям
, удовлетворяющий условиям
1) вектор  направлен так, что
направлен так, что  ,
,  ,
,  – правая тройка;
– правая тройка;
2)  ,
,  ;
;
3)  , где j – угол между векторами
, где j – угол между векторами  и
и  .
.