Пусть имеем систему линейных алгебраических уравнений
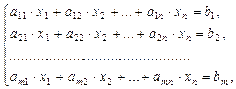 (III.5)
(III.5)
где A – матрица коэффициентов системы,  - расширенная матрица коэффициентов системы
- расширенная матрица коэффициентов системы
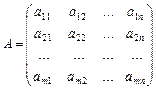 ,
, 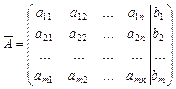 .
.
Будем считать столбцы расширенной матрицы коэффициентов векторами 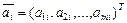 ,
, 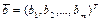 , где
, где 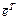 – транспонированная вектор-строка. Запишем вектор
– транспонированная вектор-строка. Запишем вектор 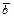 как линейную комбинацию
как линейную комбинацию
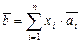 , где
, где 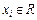 , (III.6)
, (III.6)
эта запись эквивалентна системе уравнений (III.5).
Теорема III.4 (Кронекера – Капелли). Система линейных алгебраических уравнений (III.5) совместна тогда и только тогда, когда ранг матрицы A равен рангу матрицы  , то есть
, то есть 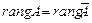 .
.
Доказательство. Необходимость. Пусть система (III.5) совместна, тогда у нее существует решение: 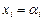 ,
,  ,
,  . Учитывая (III.6),
. Учитывая (III.6), 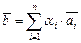 , но в этом случае
, но в этом случае 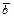 есть линейная комбинация векторов
есть линейная комбинация векторов 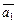 ,
,  , …,
, …,  . Следовательно, через множество векторов
. Следовательно, через множество векторов 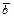 ,
, 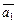 ,
,  , …,
, …,  можно выразить любой вектор из
можно выразить любой вектор из  . Это означает, что
. Это означает, что 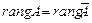 .
.
Достаточность. Пусть 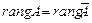 . Выберем любой базис из
. Выберем любой базис из 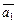 ,
,  , …,
, …,  , тогда
, тогда 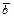 линейно выражается через базис (это могут быть как все векторы
линейно выражается через базис (это могут быть как все векторы  , так и их часть) и тем самым, через все векторы
, так и их часть) и тем самым, через все векторы  ,
,  . Это означает, что система уравнений совместна ▼.
. Это означает, что система уравнений совместна ▼.
Рассмотрим n -мерное линейное пространство L. Каждый вектор можно представить линейной комбинацией 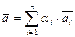 , где множество
, где множество 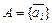 ,
,  состоит из базисных векторов. Перепишем линейную комбинацию в виде
состоит из базисных векторов. Перепишем линейную комбинацию в виде 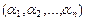 и установим взаимнооднозначное соответствие между элементами и их координатами
и установим взаимнооднозначное соответствие между элементами и их координатами
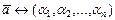 ,
,
где 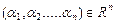 .
.
Это означает, что между n -мерным линейным векторным пространством векторов  над n -мерным полем действительных чисел
над n -мерным полем действительных чисел 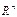 установлено взаимно-однозначное соответствие.
установлено взаимно-однозначное соответствие.
Определение. Два линейных пространства 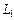 и
и 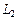 над одним и тем же скалярным полем изоморфны, если между их элементами можно установить взаимнооднозначное соответствие f, так чтобы
над одним и тем же скалярным полем изоморфны, если между их элементами можно установить взаимнооднозначное соответствие f, так чтобы
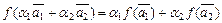 ,
,
то есть под изоморфизмом понимается взаимнооднозначное соответствие, сохраняющее все линейные отношения. Ясно, что изоморфные пространства имеют одинаковую размерность.
Из примера и определения изоморфизма следует, что с точки зрения изучения проблем линейности изоморфные пространства одинаковы, поэтому формально вместо n-мерного линейного пространства L над полем 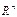 можно изучать только поле
можно изучать только поле 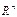 .
.
Подпространства
Линейные пространства изучают не только отношения между элементами, но и прямые, плоскости и другие линейные аналоги геометрических образов.
Определение. Непустое множество M линейного пространства L называется подпространством или линейным многообразием [11], если из принадлежности 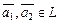 следует, что ему принадлежат все линейные комбинации
следует, что ему принадлежат все линейные комбинации 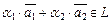 .
.
Последнее означает, что с любым элементом  оно содержит и элемент
оно содержит и элемент 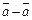 , то есть нулевой элемент
, то есть нулевой элемент 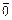 .Поэтому, говоря о подпространствах (прямых, плоскостях и т.д.), следует иметь в виду, что все они содержат нуль-вектор или проходят через начало координатной системы, если таковая введена.
.Поэтому, говоря о подпространствах (прямых, плоскостях и т.д.), следует иметь в виду, что все они содержат нуль-вектор или проходят через начало координатной системы, если таковая введена.
Следовательно, любое подпространство является пространством.
Очевидными примерами подпространства являются само пространство L и множества О, состоящее из одного элемента
{ 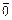 } или начала.
} или начала.
Пример III.12. Выберемв трехмерном линейном пространстве три единичных взаимно перпендикулярных вектора и приведем их к общему началу (рис. III.1), которое обозначили через O.
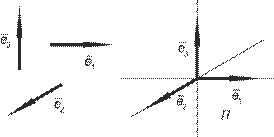
Рис. III.1
Из определения подпространства следует, что пространство  есть объединение подпространств
есть объединение подпространств  и
и  с базисами
с базисами  и
и 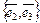 соответственно. Ясно, что
соответственно. Ясно, что 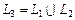 и
и 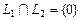 , где множество
, где множество  содержит один элемент
содержит один элемент 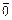 – нуль-вектор. Из рисунка видно, что
– нуль-вектор. Из рисунка видно, что  является объединением плоскости P и прямой l. Приведение к общему началу позволяет ввести прямоугольную координатную систему с заданным масштабом
является объединением плоскости P и прямой l. Приведение к общему началу позволяет ввести прямоугольную координатную систему с заданным масштабом 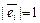 и направлением.
и направлением.
Прямые суммы
Пусть 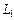 и
и 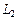 линейные пространства над одним и тем же числовым полем R. Их прямой суммой называется линейное пространство
линейные пространства над одним и тем же числовым полем R. Их прямой суммой называется линейное пространство 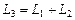 , элементами которого являются всевозможные пары элементов
, элементами которого являются всевозможные пары элементов 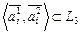 , где
, где 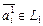 ,
, 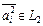 , а линейные операции определяются формулой
, а линейные операции определяются формулой
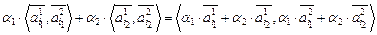 .
.
Множество всех элементов вида á  ,0ñ образует в
,0ñ образует в  подпространство, соответствие á
подпространство, соответствие á  ,0ñ®
,0ñ®  показывает, что это подпространство изоморфно
показывает, что это подпространство изоморфно 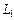 , а á0,
, а á0,  ñ –
ñ – 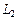 .
.
Какова связь между 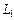 и
и 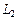 , если их рассматривать как подпространства
, если их рассматривать как подпространства 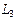 ?
?
Теорема III.5. Если 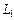 и
и 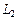 подпространства линейного пространства
подпространства линейного пространства 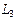 , то следующие условия эквивалентны
, то следующие условия эквивалентны
1) 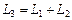 ;
;
2) 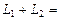 Ơ, где Ơ ={0} – нуль-пространство и
Ơ, где Ơ ={0} – нуль-пространство и 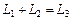 (то есть
(то есть 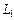 и
и 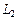 дополняют друг друга);
дополняют друг друга);
3) любой элемент 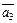 из
из 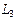 можно записать как
можно записать как 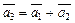 , где
, где 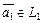 ,
, 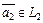 (рис. III.2).
(рис. III.2).
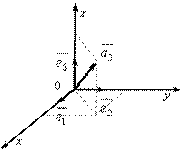
Рис. III.2
Теорема III.6. Размерность прямой суммы равна сумме размерностей ее слагаемых.
Следствие. Любое подпространство конечного линейного пространства обладает дополнением.
Пример III.13. Пусть элементы  ,
,  ,
, 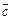 ,
, 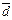 принадлежат
принадлежат 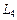 , а
, а 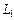 и
и 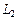 подпространства такие, что
подпространства такие, что 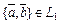 ,
, 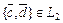 .
.
Проверить равенство 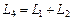 , если
, если
а) 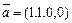 ,
, 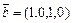 ,
, 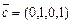 ,
, 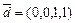 ;
;
б) 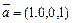 ,
,  ,
, 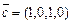 ,
, 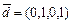 .
.
Имеем 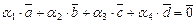 или
или
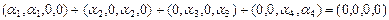 .
.
По правилу сложения координат получили а) 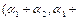
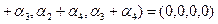 . Приравнивая соответствующие координаты правой и левой частей последнего равенства, получим систему уравнений, решение которой имеет вид:
. Приравнивая соответствующие координаты правой и левой частей последнего равенства, получим систему уравнений, решение которой имеет вид: 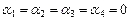 , то есть элементы линейно независимые. Рассматривая пары
, то есть элементы линейно независимые. Рассматривая пары 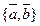 ,
, 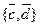 , получаем
, получаем 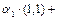
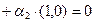 Þ
Þ 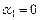 ,
, 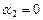 . Таким образом, равенство
. Таким образом, равенство 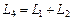 верно.
верно.
Аналогичные вычисления для случая б) дают 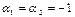 ,
, 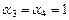 , то есть элементы линейно зависимые,
, то есть элементы линейно зависимые, 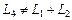 .
.
Докажем теорему (о размерности пространства), используя разложение пространства в прямую сумму подпространств.
Теорема III.7. Все базисы n -мерного линейного пространства  состоят из n элементов.
состоят из n элементов.
Доказательство. Рассмотрим n -мерное линейное пространство  ,
,  . Доказательство проведем методом математической индукции.
. Доказательство проведем методом математической индукции.
При 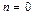 число базисных векторов равно 0, что следует из определения линейной комбинации. При
число базисных векторов равно 0, что следует из определения линейной комбинации. При  число базисных элементов
число базисных элементов  равно
равно 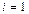 . Любой другой элемент получается умножением базисного на число
. Любой другой элемент получается умножением базисного на число 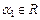 , то есть
, то есть 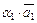 , следовательно, базис одномерного линейного пространства (прямая) состоит из одного элемента.
, следовательно, базис одномерного линейного пространства (прямая) состоит из одного элемента.
Предположим, что n -мерное линейное пространство  состоит из n базисных элементов. Докажем, что n +1-мерное линейное пространство
состоит из n базисных элементов. Докажем, что n +1-мерное линейное пространство 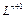 состоит из (n +1) базисного элемента. В самом деле, представим (n +1)-мерное пространство
состоит из (n +1) базисного элемента. В самом деле, представим (n +1)-мерное пространство 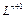 в виде прямой суммы подпространств
в виде прямой суммы подпространств 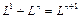 , где
, где 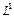 – одномерное линейное пространство, что возможно в силу предыдущей теоремы. Любой элемент пространства
– одномерное линейное пространство, что возможно в силу предыдущей теоремы. Любой элемент пространства  получается умножением базисных элементов
получается умножением базисных элементов 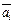 на число
на число  ,
, 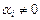 ,
,  . В силу свойств прямой суммы получаем, что любой базис пространства
. В силу свойств прямой суммы получаем, что любой базис пространства 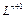 состоит из n +1 элемента и число базисов в любом линейном пространстве
состоит из n +1 элемента и число базисов в любом линейном пространстве  бесконечно ▼.
бесконечно ▼.
Замечание. Между прочим, доказательство по индукции можно было начинать с 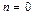 , не акцентируя внимание на
, не акцентируя внимание на  .
.
Замечание. Из теоремы, в силу метода индукции, следует, что потенциально любое линейное пространство содержит столько базисных векторов, какова его размерность.
Пример III.14. Рассмотрим три единичных взаимно перпендикулярных вектора  ,
,  ,
, 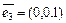 . С точностью до изоморфизма возможно разложение в прямую сумму
. С точностью до изоморфизма возможно разложение в прямую сумму 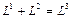 по базисным векторам для
по базисным векторам для 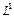 любой из
любой из 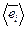 , для
, для 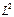 – любая пара
– любая пара 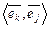 ,
, 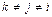 . Аналогично можно составить базис бесконечномерного пространства.
. Аналогично можно составить базис бесконечномерного пространства.
Евклидовы пространства
Определяя линейные пространства аксиоматически, то есть абстрактно, мы для наглядности пользовались обозначениями векторных пространств, что позволило нам более отчетливо представлять свойства линейных. Эффективность этого факта проявляется и в Евклидовых пространствах.
До сих пор мы изучали качественною сторону линейных пространств, то есть строение и взаимную зависимость элементов. Перейдем к изучению их другой стороны – количественным отношениям между элементами, их измерениям. По геометрическим изображениям не более чем для 3-мерных векторных пространств мы можем количественно сравнивать векторы по длине, углу, определять расстояния между ними и т.д. Однако для пространств большей размерности такой подход неприменим, а метод аналогий ненадежен, поскольку в них уже отсутствует наглядность. Хотелось бы внутри произвольных векторных (линейных) пространств иметь такое понятие, которое было бы неизменяемым (инвариантным) при линейных преобразованиях векторов. Такое понятие, являющееся отображением векторного пространства в свое скалярное поле, называется скалярным или внутренним произведением.
Будем рассматривать линейные пространства над основным скалярным полем – полем действительных чисел R. Это наиболее важная практическая часть свойств линейных пространств. Именно здесь и проявляется более всего необходимость геометрической интерпретации их векторными.
Определение. В n -мерном линейном (вещественном) пространстве L определено скалярное умножение, если любой паре элементов 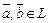 поставлено в соответствие действительное число
поставлено в соответствие действительное число 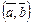 , называемое скалярным произведением элементов
, называемое скалярным произведением элементов  ,
,  , определяемое аксиомами
, определяемое аксиомами
1) 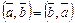 ;
;
2) 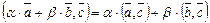 ,
, 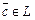 ,
,  ;
;
3) 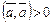 , если
, если 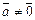 и
и 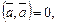 если
если  .
.
Из аксиомы 2 следует, что 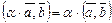 , тогда, если
, тогда, если  , то
, то 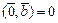 , то есть скалярное умножение нулевого элемента и любого элемента линейного пространства равно 0.
, то есть скалярное умножение нулевого элемента и любого элемента линейного пространства равно 0.
По определению положим 
Пусть 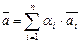 ,
, 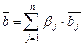 ,
, 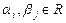 , тогда, опираясь на аксиому 2, получим
, тогда, опираясь на аксиому 2, получим
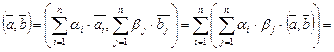
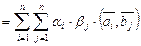 . (III.7)
. (III.7)
Линейное пространство, в котором определено скалярное умножение, называется Евклидовым [3].
Пример III.15. Пусть в L задан базис из единичных векторов 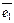 ,
, 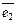 , …,
, …, 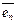 , для которых скалярное произведение
, для которых скалярное произведение  , если
, если  и
и 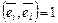 . Тогда, как следует из (III.7),
. Тогда, как следует из (III.7),
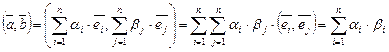 .
.
Выполнение аксиом 1) – 3) очевидно, то есть правая часть полученной формулы определяет скалярное умножение.
Следовательно, скалярное произведение можно вычислить по формуле
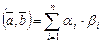 . (III.8)
. (III.8)
Упражнение. Проверить выполнение аксиом 1) – 3) для формулы (III.8).
Формула (III.7) обобщает аксиому 2) скалярного произведения на случай, когда в качестве базисных векторов выбраны произвольные векторы, однако если базисные векторы единичны и их попарное скалярное произведение равно 0 (то есть, 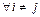 ,
,  , как в формуле (III.8)), то формулу (III.8) можно принять за определение скалярного произведения, хотя здесь мы привязаны к ортогональному базису.
, как в формуле (III.8)), то формулу (III.8) можно принять за определение скалярного произведения, хотя здесь мы привязаны к ортогональному базису.
Видно, что в n -мерном пространстве скалярное умножение можно задать различными способами; все зависит от выбранного базиса. Тем не менее можно говорить, что в n -мерном векторном пространстве существует, в некотором смысле, о котором будем говорить ниже, единственное n -мерное Евклидово пространство. Подтвердим сказанное определениями, являющимися свойствами аксиом скалярного произведения.
Определение. Ненулевые векторы  ,
,  называются ортогональными, если их скалярное произведение равно 0, т.е.
называются ортогональными, если их скалярное произведение равно 0, т.е. 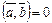 .
.
Нуль-вектор ортогонален любому вектору.
Определение. Система векторов называется ортогональной системой, если все ее векторы ортогональны между собой.
Всякая ортогональная система ненулевых векторов линейно независима [3, 11].
Ранее, основываясь на знаниях разделов школьной математики, в примерах мы рассматривали векторы, заданные координатами, и это не вызывало сомнений в справедливости такого задания. Далее будет показана непосредственная связь между различными координатными системами и скалярным произведением, здесь же отметим следующие два свойства Евклидова пространства [4, 5].
1. Всякое Евклидово пространство обладает ортогональными базисами, причем любой ненулевой вектор входит в состав некоторого ортогонального базиса.
Важным видом ортогональных базисов, соответствующих прямоугольным декартовым координатам, являются ортонормированные базисы, 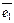 ,
, 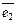 , …,
, …, 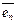 .
.
Определение. Вектор  называется нормированным, если его скалярное умножение на себя равно единице, то есть
называется нормированным, если его скалярное умножение на себя равно единице, то есть
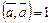 .
.
Если 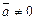 , то его нормированием называется вектор
, то его нормированием называется вектор 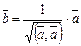 .
.
Определение. Базис 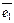 ,
, 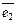 , …,
, …, 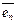 n -мерного Евклидового пространства называется ортонормированным, если он
n -мерного Евклидового пространства называется ортонормированным, если он
а) ортогонален, т.е.  ,
, 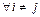 ;
;
б) нормирован, т.е. 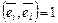 ,
, 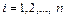 .
.
Всякое Евклидово пространство обладает ортонормированным базисом.
Определение. Евклидовы пространства 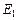 и
и 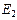 называются изоморфными, если между их векторами можно установить взаимно-однозначное соответствие, такое, что выполняются
называются изоморфными, если между их векторами можно установить взаимно-однозначное соответствие, такое, что выполняются
а) 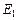 и
и 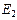 изоморфны в смысле изоморфизма их как линейных пространств: сохраняются все линейные соотношения;
изоморфны в смысле изоморфизма их как линейных пространств: сохраняются все линейные соотношения;
б) сохраняется скалярное произведение, то есть
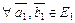 и
и 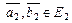 Þ
Þ 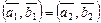 ,
,
если образами векторов 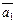 ,
, 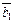 являются векторы
являются векторы 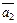 ,
, 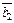 соответственно.
соответственно.
2. Отсюда следует, что любые Евклидовы пространства одинаковой размерности изоморфны. Обратное тоже справедливо.
Пример III.16. Доказать, что если скалярное произведение любых двух векторов конечного Евклидова пространства выражается формулой (III.8), то базис, относительно которого взяты координаты, является ортонормированным.
Решение. Пусть 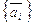 ,
, 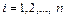 , базис n -мерного Евклидова пространства
, базис n -мерного Евклидова пространства  и
и 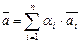 ,
, 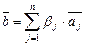 . Сначала покажем, что он ортогонален. Имеем по формуле (III.7)
. Сначала покажем, что он ортогонален. Имеем по формуле (III.7)
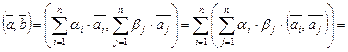
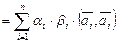 .
.
Отсюда следует, что, если  , то
, то 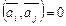 , поэтому базис ортогонален.
, поэтому базис ортогонален.
Покажем, что он нормирован. Учитывая условие (формула (III.8)), получаем

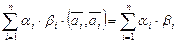 .
.
Отсюда 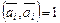 ,
,  , то есть базис нормированный.
, то есть базис нормированный.
Выполнение обоих условий ортонормированности базиса доказано ▼.
Координатные системы
Координатные системы или системы координат – от латинских слов coordinatus – совместно, ordinatus – упорядоченный [3] (см стр. 78, [11]).
При решении различных задач, возникающих из потребностей практики, часто требуется знать характеристики положения тела в пространстве, его протяженность, взаимное расположение с другими телами и т.д.
Из соображений практической целесообразности часто требуется рассматривать тело как точку на прямой, плоскости или в пространстве, а ее движение описывать вектором. Положение такой точки в пространстве можно полностью определить ее координатами относительно любого базиса, то есть упорядоченным набором чисел.
Пусть дана направленная геометрическая прямая линия (рис. III.3).

Рис. III.3.
Рассмотрим линейное пространство L векторов  на прямой. Зафиксируем на ней начало O и единичный вектор
на прямой. Зафиксируем на ней начало O и единичный вектор 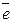 , где
, где  . Положение любой точки M на прямой, очевидно, однозначно определяется вектором
. Положение любой точки M на прямой, очевидно, однозначно определяется вектором  . Все векторы на прямой коллинеарны, следовательно, существует число
. Все векторы на прямой коллинеарны, следовательно, существует число  , такое, что
, такое, что 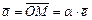 . Число a называется аффинной координатой. Таким образом, каждая точка M на прямой, в самом деле, однозначно определяется аффинной координатой a. При фиксированной аффинной системе координат существует однозначное соответствие между всеми действительными числами (числовая ось) и точками прямой линии.
. Число a называется аффинной координатой. Таким образом, каждая точка M на прямой, в самом деле, однозначно определяется аффинной координатой a. При фиксированной аффинной системе координат существует однозначное соответствие между всеми действительными числами (числовая ось) и точками прямой линии.
В одномерном пространстве мы уже можем вычислять расстояние между двумя точками 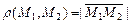 , геометрически интерпретируя его как длину отрезка. В самом деле, из аксиом линейного пространства имеем
, геометрически интерпретируя его как длину отрезка. В самом деле, из аксиом линейного пространства имеем 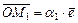 ,
, 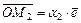 , тогда
, тогда  , отсюда длина
, отсюда длина 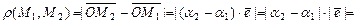
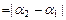 .
.
Аналогично рассмотрим плоскость, на которой зафиксируем начало и неколлинеарные единичные векторы  ,
, 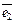 с общим началом, тогда получаем аффинную систему координат (рис. III.4), в которой любой вектор
с общим началом, тогда получаем аффинную систему координат (рис. III.4), в которой любой вектор 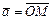 однозначно определяется двумя координатами
однозначно определяется двумя координатами 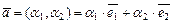 ,
, 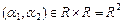 .
.
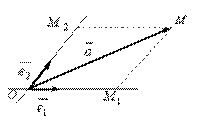
Рис. III.4
Векторы 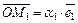 ,
, 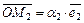 , а
, а 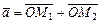 . Тогда M 1 и M 2 называются аффинными проекциями вектора
. Тогда M 1 и M 2 называются аффинными проекциями вектора  на оси координат
на оси координат 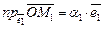 ,
, 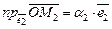 . Если
. Если 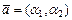 , то
, то 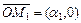 ,
, 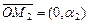 . Каждый базисный вектор на своей оси образует собственную одномерную систему координат.
. Каждый базисный вектор на своей оси образует собственную одномерную систему координат.
Задание упорядоченной пары чисел 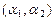 однозначно определяет точку плоскости. Следовательно, при заданной системе координат существует взаимно-однозначное соответствие между всеми упорядоченными парами вещественных чисел и точками плоскости.
однозначно определяет точку плоскости. Следовательно, при заданной системе координат существует взаимно-однозначное соответствие между всеми упорядоченными парами вещественных чисел и точками плоскости.
Аналогично вводится аффинная система координат в пространстве с базисными векторами  ,
, 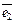 ,
, 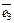 . Положение любой точки M в пространстве однозначно определяется вектором
. Положение любой точки M в пространстве однозначно определяется вектором 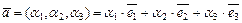 , где
, где 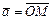 , а координаты называются
, а координаты называются  – абсциссой,
– абсциссой, 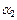 – ординатой,
– ординатой, 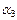 – аппликатой точки M. Соответствующим образом определяются проекции на оси.
– аппликатой точки M. Соответствующим образом определяются проекции на оси.
Заметим, что проекцию точки в пространстве можно задать и на координатной плоскости.
Среди аффинных координат наибольшее распространение получили декартовые координаты, характеризующиеся тем, что базисные единичные векторы взаимно ортогональны и обычно обозначаются буквами 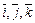 . Их преимущество по сравнению с другими координатными системами только в простоте получаемых формул, отражающих измерения и взаимное расположение объектов в линейных пространствах.
. Их преимущество по сравнению с другими координатными системами только в простоте получаемых формул, отражающих измерения и взаимное расположение объектов в линейных пространствах.
Метод координат – хорошо разработанный аппарат, исследующий геометрические объекты алгебраическими и математического анализа методами. Этот метод лежит в основе аналитической геометрии – прикладной математической науки, изучающей геометрические объекты аналитическими методами.
Как уже отмечалось, линейная алгебра широко применяется в различных науках, и ее связь с аналитической геометрией вполне естественна. Можно сказать, что линейная алгебра является ее теоретической базой. В дальнейшем эта связь будет постоянно подтверждаться.
IV. Векторная алгебра
Векторы
Величина, которая полностью определяется своим числовым значением, называется скалярной или скаляром (термин ввел У. Гамильтон в 1843 г.). Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора, который ранее уже использовался в примерах.
Вектор – это направленный отрезок. Если А – начало вектора, а В – его конец, то вектор обозначается символом  или
или  . Вектор,
. Вектор, 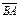 называется противоположным вектору
называется противоположным вектору  . Вектор противоположный вектору
. Вектор противоположный вектору  ,обозначается (
,обозначается (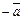 ).
).
Длиной вектора  называется длина отрезка
называется длина отрезка 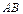 и обозначается
и обозначается 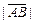 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 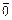 (или 0, когда нет сомнений в понимании обозначения). Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным и обозначается через
(или 0, когда нет сомнений в понимании обозначения). Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным и обозначается через  . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  . Векторы
. Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Два вектора  и
и  называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.
называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку O пространства, то есть векторы определены с точностью до параллельного переноса.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.