Пусть дана ось Ox и векторы 
и 
:
, 
.
Тогда, как следует из свойств сложения векторов, имеем
1) 
;
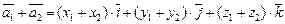2) 
, 
.
Отсюда, как следует из (IV.2), получаем
a)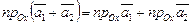 
;
b) 
.
Координаты вектора
Найдем координаты вектора 
, если известны координаты точек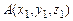 
и 
. Имеем:
.
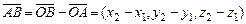Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала.
Зададим в пространстве декартову систему координат Oxyz и вектор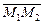 
, где координаты точек 
, 
.
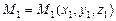Проекция вектора 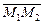на ось Ox (рис. IV.6) определяется
. (IV.6)
Рис. IV.6.
Тригонометрическая формула (IV.6) устанавливает связь между геометрическим образом отрезка и его проекцией на ось Ox, которая в алгебраической форме имеет вид
. (IV.7)
Знак правой части в (IV.7) определяетс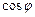я 
, для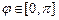 
. Таким образом,
, (IV.8 а)
, (IV.8 б)
. (IV.8 в)
Для нахождения длины отрезка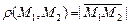 
воспользуемся теоремой Пифагора, получим
. (IV.9)
Деление отрезка в данном отношении
Рассмотрим в пространстве вектор 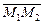(рис. IV.7). Пусть M – внутренняя точка направленного отрезка, тогда 
. Число l называется отношением, в котором точка M делит отрезок .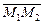
Вычислим координаты точки 
, которая делит отрезок 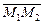в отношении l, где , .
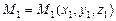Учитывая формулы (IV.8 а) – (IV.8 в), получаем
.
Приравнивая последовательно дроби к числу l, будем иметь
, 
, 
. (IV.10)
Формулы (IV.10) называются формулами деления отрезка в отношении l.
Пример IV.1. Для деления отрезка пополам, полагая 
, получаем координаты точки 
.
Замечание. Для положительных значений l точка M лежит между точками M 1 и M 2, для отрицательных – вне отрезка 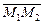. Для 
формула (IV.10) не имеет смысла.
Упражнение. Получить формулы (IV.5), используя преобразование подобия.
Пример IV.2. Начало вектора находится в точке 
, конец в точке 
. Найти координаты вектора 
, его длину и направление.
Решение. Для того, чтобы найти координаты вектора ,нужно от координат конца вычесть координаты начала вектора:
.
Найдем длину вектора: 
.
Теперь по формулам (IV.10) имеем: 
, 
, 
.
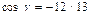Базис системы векторов
Определение. Система векторов 
, 
, 
называется линейно зависимой, если существуют такие константы 
, 
, 
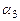, не все равные нулю, что имеет место равенство
.
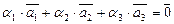Если из этого равенства с необходимостью следует, что если 
, то система называется линейно независимой.
Определение. Базисом в 3-х мерном пространстве называется любая упорядоченная система из трех линейно независимых векторов пространства (см стр. 77, § 2).
Теорема IV.1. Векторы 
, 
, 
Î L 3 образуют базис тогда и только тогда, когда
D¹0, где 
.
Доказательство.
1) Необходимость. Пусть векторы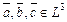 
образуют базис, тогда по определению эти векторы линейно независимые, а следовательно, равенство
,
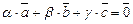которое эквивалентно однородной системе
выполняется только в случае 
. Однородная система линейных алгебраических уравнений имеет единственное нулевое решение только в том случае, когда
.
По 1-му свойству определителей получаем
.
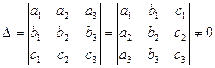Необходимость доказана.
2) Достаточность. Пусть для векторов 
, 
, 
пространства L 3 выполняется
.
Проверим линейную независимость векторов 
, составим равенство 
, рассмотрим однородную систему уравнений
так как определитель, составленный из коэффициентов при неизвестных системы, не равен нулю, т.е.
,
то эта система имеет единственное нулевое решение, по определению, векторы образуют систему линейно независимых векторов, а, следовательно, и базис в пространстве L 3. Теорема доказана.
Если векторы 
, 
, 
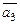образуют базис, а вектор 
представляется в виде 
, тогда числа , , 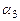называются координатами вектора в базисе , , , 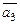то есть 
.
Пример IV.3. Даны три векторы 
, 
, 
. Показать, что они образуют базис, и найти разложение вектора 
в этом базисе.
Решение. Покажем, что вектора 
, 
, 
образуют базис. Вычислим определитель, составленный из координат этих векторов:
.
Так как D¹0, то, по теореме IV.1, векторы , , образуют базис. Отсюда получаем разложение вектора 
по базисным векторам , , :
Û 
.
Чтобы найти координаты , , 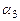вектора в новом базисе, необходимо найти решение следующей системы уравнений:
Решим эту систему методом Крамера, имеем
, 
,
, 
.
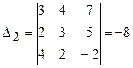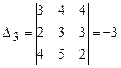Так как D¹0, то система совместна и имеет единственное решение: 
, 
, 
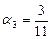. То есть
.
Определение. Совокупность всех 3-х мерных векторов с действительными координатами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число, образует 3-х мерное векторное пространство.