Пусть даны три точки 
, 
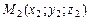и 
. Если точки не лежат на одной прямой, то через них всегда можно провести единственную плоскость. Обозначим (х, у, z) координаты произвольной точки М пространства и рассмотрим три вектора: 
, 
, 
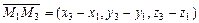. Точка М лежит на плоскости М 1 М 2 М 3 в том и только в том случае, когда перечисленные три вектора компланарны, а значит 
, т.е. определитель, составленный из их координат, равен нулю:
.
Пример V.5. Написать уравнение плоскости, проходящей через точки 
, 
и 
.
Решение. Пусть 
– произвольная точка плоскости,
тогда векторы 
, 
, 
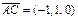компланарны, поэтому:
Вычисляя определитель по правилу треугольников, получим: 
или 
.
Теорема V.1. В пространстве 
всякая плоскость выражается уравнением первой степени 
, 
.
Доказательство. В предыдущем пункте было установлено, что всякая плоскость может быть задана уравнением вида (V.4):
, 
.
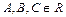Раскрыв скобки и обозначив 
, получим общее уравнение первой степени относительно x, y, z: 
, эквивалентное уравнению (V.4). Поэтому оно определяет ту же плоскость, что и уравнение (V.4), и называется общим уравнением плоскости. Коэффициенты при переменных в этом уравнении сохраняют тот же геометрический смысл, что и в равенстве (V.4), то есть являются координатами нормального вектора 
плоскости. Так как нормальный вектор плоскости является ненулевым, то коэффициенты A, B и C не могут быть одновременно равны нулю. Итак, мы доказали, что всякая плоскость в определяется уравнением первой степени относительно переменных координат x, y, z.
Теорема V.2 (обратная). Всякое линейное уравнение с тремя переменными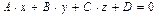 
, 
, определяет плоскость в пространстве 
, если хотя бы один из коэффициентов при переменных не равен нулю.
Доказательство. Пусть x 0, y 0, z 0 – какое-либо решение данного уравнения. Тогда 
, откуда 
. Подставляя в данное уравнение вместо D его значение и группируя члены, получим
|
|
.
Это уравнение плоскости, проходящей через точку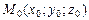 
и имеющей нормальный вектор . Следовательно, и равносильное ему уравнение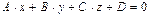 
определяет плоскость [перпендикуляр-ную вектору ].
Пример V.6. Построить в прямоугольной системе координат плоскость, заданную уравнением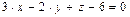 
.
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три ее точки (не лежащие на одной прямой), например точки пересечения плоскости с осями координат. Полагая в заданном уравнении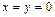 
, получим 
. Следовательно, заданная плоскость пересекает ось Oz в точке 
. Аналогично, при 
получим 
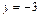, то есть точку 
; при 
получим 
, то есть точку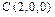 
. По трем точкам , , 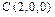строим заданную плоскость (рис. V.6).
Частные случаи общего уравнения плоскости. Рассмотрим особенности расположения плоскости в тех случаях, когда те или иные коэффициенты общего уравнения обращаются в нуль.
1. При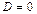 
уравнение 
определяет плоскость, проходящую через начало координат, так как координаты точки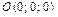 
удовлетворяют этому уравнению.
2. При 
уравнение 
определяет плоскость, параллельную оси Ох, поскольку нормальный вектор 
этой плоскости перпендикулярен оси Ох (его проекция на ось Ох равна нулю). Аналогично при 
плоскость 
параллельна оси Оу, а при 
плоскость 
параллельна оси Оz.
3. При 
уравнение 
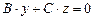определяет плоскость, проходящую через ось Ох, поскольку она параллельна оси Ох (
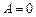) и проходит через начало координат (
). Аналогично плоскость 
проходит через ось Оу, а плоскость 
– через ось Оz.
|
|
4. При 
уравнение 
определяет плоскость, параллельную координатной плоскости Оxу, поскольку она параллельна осям Oх (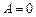) и Оу (
). Аналогично, плоскость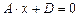 
параллельна плоскости уОz, а плоскость 
– плоскости Оxz.
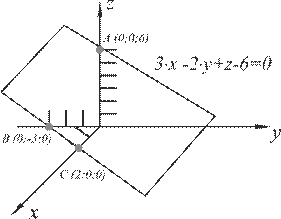
Рис. V.6
5. При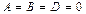 
уравнение 
(или 
) определяет координатную плоскость Оxу, так как она параллельна плоскости Оxу (
) и проходит через начало координат (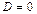). Аналогично уравнение 
в пространстве определяет координатную плоскость Оxz, а уравнение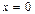 
– координатную плоскость Оyz.
Пример V.7. Составить уравнение плоскости P, проходящей через ось Оу и точку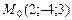 
.
Решение. Уравнение плоскости, проходящей через ось Оу, имеет вид 
. Для определения коэффициентов A и C воспользуемся тем, что точка 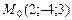принадлежит плоскости P. Поэтому ее координаты удовлетворяют написанному выше уравнению плоскости: 
Û 
, откуда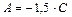 
. Подставив найденное значение A в уравнение , получим: 
, или 
.
Это и есть искомое уравнение.