Пусть A, B – линейные операторы и 
– произвольный вектор, тогда их сумма есть оператор C, определяемый как
,
кроме того, 
.
Обозначим для каждого A через (–A) оператор, определенный как 
, тогда 
. Добавив свойство коммутативности и ассоциативности сложения, получим, что линейный оператор образует коммутативную группу по сложению (выполняются аксиомы 1 – 4 линейных пространств).
Для любого A и 
определим произведение 
как 
. Легко показать выполнение других аксиом линейного пространства. Тем самым справедливо: множество всех линейных операторов образует линейное (векторное) пространство.
Умножение операторов
Оператор C называется произведением оператора A на оператор B и определяется как
.
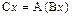Произведение линейных операторов – линейный оператор. В самом деле, 
и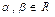 
, имеем
. ▼
Далее, аналогично, показывается, что для любых операторов A, B, C и , выполняется
1) 
;
2) 
;
3) 
;
4) 
Покажем, например, выполнение 4). Имеем 
,
. ▼
Таким образом, множество линейных операторов образует некоммутативное кольцо.
Замечание. У линейных операторов имеется два «нехороших» свойства. Первое из них, это некоммутативность произведения, второе состоит в том, что может оказаться равным нулю произведение двух операторов даже тогда, когда ни один из них не равен нулю (ненулевой оператор, произведение которого с некоторым ненулевым оператором равно нулю, называется делителем нуля). Необходимость учитывать эти свойства часто приводит к путаницам, в частности в обозначениях (например, 
– это 
или 
, и т.д.).
К счастью, у линейного оператора есть и «хорошие» свойства, например, если оператор A обладает хотя бы одним из свойств:
1) если 
, то 
;
2) 
Þ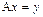 
.
Если A обладает обоими этими свойствами, то говорят, что A – обратим. Обратный к A оператор обозначается символом 
.
Теорема. Если A, B, C – линейные операторы, такие, что 
, то A обратим и 
, то есть
.
Перейдем к количественной характеристике линейных операторов.
Пусть 
базис в L и A линейный оператор в нем. В результате действия оператора на базисные векторы получаются новые векторы 
, которые также образуют базис:
, 
.
Предположим, что векторы 
нового базиса выражаются
через векторы 
старого базиса как
, 
. (VI.3)
Полученная система линейных алгебраических уравнений (VI.3) очевидно удовлетворяет условиям линейности (VI.1).
Особенностью этих преобразований является линейность функций, связывающих старые и новые базисные векторы. Коэффициенты 
определяют матрицу 
, называемую матрицей линейного оператора.
Таким образом, в базисе 
каждому линейному оператору соответствует определенная матрица и обратно, каждой матрице отвечает некоторый линейный оператор, определяемый формулой (VI.3). Матричное исчисление для изучения линейных операторов в конечномерных векторных пространствах является наиболее удобным алгебраическим аппаратом, конечно, если матрицы согласованы.
Умение находить сумму и произведение операторов, позволяет получать результат возведения оператора в любую степень, найти любой полином от оператора A, как
.
Оператором, обратным к A, называется оператор , такой, что выполняется
.
Вырожденным операторам, не имеющим обратного, соответствуют особые (вырожденные) матрицы, определители которых равны 0.
Пример VI.2. Определить, для каких матриц существуют обратные:
, 
, 
.
Решение 1. Вычислим ранги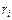 
, 
, матриц. Получим по порядку 
, 
, 
.
Решение 2. Вычислим определители матриц: 
, 
.
Таким образом, невырожденной матрицей является первая матрица 
.
Тот факт, что множество всех линейных операторов образует векторное пространство, далеко не единственное достоинство операторов. Например, из последнего следует, что для них вполне удовлетворительно определено умножение (см алгебру матриц).
Матрицы операторов
Пусть в некоторой фиксированной координатной системе , известны матрицы 
, 
операторов A, B, соответственно.
Определим матрицу оператора 
, где 
покажем, что 
.
Имеем
. ▼
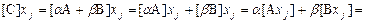
Пусть 
, тогда
.
.
Отсюда .
Итак, имея базис , мы поставили в соответствие каждому линейному оператору A матрицу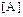 
, тогда
.
Соответствие взаимнооднозначное, и матрица является матрицей некоторого оператора, то есть если 
, то
.
Таким образом, если 
, то
.
Подведем итоги, пусть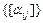 
, 
и т.д. множество всех матриц. Определим сумму, умножение на число, произведение, 
– матрицу нулевого оператора, 
– матрицу тождественного оператора формулами
, 
,
, 
, 
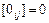Тогда соответствие между всеми линейными операторами A на L и всеми матрицами , задаваемыми как , является изоморфизмом.
Пример VI.3. Пусть A линейный оператор на множестве
многочленов степенине большей, чем n -1, 
, 
, определенный формулой 
и 
– базис
в M, определенный формулой 
, 
. Найти матрицу оператора A, где 
в базисе 
.
Решение. Если 
, 
, то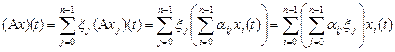 
Отсюда 
, 
. Применяя формулу бинома Ньютона, 
, для каждого фиксированного j, приравнивая коэффициенты при одинаковых степенях 
, получим
.
Учитывая, что 
, причем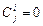 
для 
, где 
, получим матрицу оператора A
, 
.
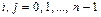В частности, для случая 
. ▼
Покажем, как, зная матрицу линейного оператора A по координатам вектора x, найти координаты образа A x в этом базисе.
Пусть , тогда, в обозначениях примера, 
, что равносильно матричному равенству
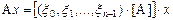, (VI.4)
где в квадратных скобках стоит произведение вектора (можно матрицы-строки) на матрицу оператора A.
Отсюда следует, что строка координат вектора 
равна строке координат вектора x, умноженной справа на матрицу 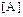, все в базе 
.
Пример VI.4. В условиях предыдущего примера, найти координаты образа при известной , где .
Решение. Имеем , тогда 
. По-прежнему ограничимся случаем , где базис 
, тогда
.
Окончательно,
. ▼
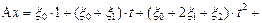
Изменение базиса [3, 11]
Дадим ответ на решение задач, часто возникающих при изменении базиса.
Пусть , 
, , – два базиса в n -мерном линейном пространстве L.
I (a). Если вектор 
, то какова связь между его координатами в базисе и его координатами 
в базисе ?
I (b). Если 
– упорядоченное множество скаляров, то какова связь между векторами x и y?
Пусть A – линейный оператор, определяемый равенствами
,
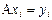положим 
, 
, тогда 
.
Ответы:
(a). Пусть – матрица оператора A в базисе , то есть 
, 
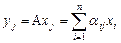. Оператор A обратим, поскольку из 
, следует, что 
, . Так как
,
то
.
(b). Очевидно, что 
. Это означает следующее: если матрица 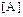оператора A известна, то ее строки можно рекомендовать рассматривать как преобразование координат, а можно как преобразование векторов.
Подобие [11]
II (a). Пусть B – линейный оператор на L. Какова связь между его матрицами и 
в базисах и соответственно?
II (b). Дана матрица . Какова связь между линейными операторами B и C, определенными равенствами 
и 
соответственно?
Ответы:
a) Имеем 
, . С использованием оператора A можем записать
.
А также
.
Учитывая предыдущее выражения, стоящие в правых частях, получаем
.
Или, переходя к матрицам, имеем равенство
.
Матрица 
соответствует оператору B в базисе и для ее вычисления, учитывая, что оператор A обратим, умножим слева матричное уравнение на матрицу 
. Учитывая, что
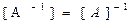и 
,
получаем
.▼
В этом случае говорят, что матрицы и 
подобны.
б). Заметим, что 
и
,
то есть оператор C таков, что
или
, тогда 
.
Линейные операторы C и B называются подобными, если существует обратимый оператор A, удовлетворяющий этому равенству.
Пример VI.5. Доказать, что а) если A подобен скаляру a, то 
; b) если A и B подобны, то это же верно и для 
и 
, а если A и B обратимы, то подобны и 
и 
.
Решение. а) Пусть E – тождественный оператор, тогда, по определению, 
. Далее существует оператор C, что 
, тогда 
и, по теореме об обратимости оператора,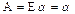 
, то есть . ▼
b) имеем 
, тогда 
. ▼
Пусть A и B обратимы, тогда имеем . Заметим, что для любых обратимых матриц, 
, тогда
. ▼