Любая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду, определенному формулой
 , (VII.5)
, (VII.5)
где форма f ранга  от n неизвестных; числа,
от n неизвестных; числа, 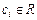 , считаются положительными, но часть слагаемых формулы (VII.5) могут быть отрицательными.
, считаются положительными, но часть слагаемых формулы (VII.5) могут быть отрицательными.
При таком условии заменой 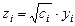 ,
, 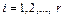 ; и
; и  ,
,  невырожденное линейное преобразование приводит квадратичную форму к нормальному виду, то есть
невырожденное линейное преобразование приводит квадратичную форму к нормальному виду, то есть
 . (VII.6)
. (VII.6)
Общее число квадратов равно рангу квадратичной формы.
Существует много линейных преобразований, приводящих квадратичную форму к нормальному виду (VII.6), но с точностью до расположения знаков такое приведение единственное [3, 7].
Для квадратичных действительных форм выполняется закон инерции. Число положительных и отрицательных квадратов в нормальном виде, к которому приводится данная квадратичная форма с действительными коэффициентами действительным линейным преобразованием, не зависит от выбора этого преобразования.
Число положительных (отрицательных) квадратов в нормальной форме формы f называется положительным (отрицательным) индексом инерции (в формуле (VII.6) это k), разница между положительными и отрицательными индексами инерции называется сигнатурой формы f (в формуле (VII.6) она равна r - k).
Пусть дана квадратная матрица 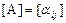 размерности n квадратичной формы f. Миноры, расположенные по главной диагонали этой матрицы, порядков 1, 2, …, n, последний из них совпадает с определителем матрицы
размерности n квадратичной формы f. Миноры, расположенные по главной диагонали этой матрицы, порядков 1, 2, …, n, последний из них совпадает с определителем матрицы 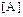 ,
,  , то есть
, то есть
 ,
,  , …,
, …,  ,
,
называются главными минорами формы f.
Теорема VII.1. Квадратичная форма f от n неизвестных с действительными коэффициентами тогда и только тогда будет состоять из положительных членов, когда все главные миноры положительны.
Пример VII.3. Квадратичная форма

положительно определена, так как все главные миноры матрицы 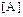 положительны:
положительны:
 ,
,  ,
, 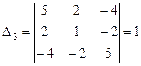 .
.
Приводить квадратичную форму к каноническому виду можно, как уже отмечалось, многими способами, но нормальный вид один. Покажем это на примере.
Пример VII.4. Привести к каноническому виду квадратичную форму  [7].
[7].
Решение. Зададим линейное преобразование:
1)  тогда получим
тогда получим  .
.
Для другого преобразования имеем
2) 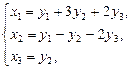 тогда получим
тогда получим 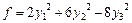 .
.
Нормальный вид квадратичной формы, которому соответствуют оба канонических вида,  .
.
Упражнение. Проверить справедливость полученных формул непосредственной подстановкой преобразований 1) и 2) в исходную квадратичную форму.
Вполне естественно возникает вопрос: «Как найти матрицу линейного преобразования (оператора)?»
Прежде чем перейти к рассмотрению следующего примера, дадим некоторые пояснения. Не нарушая сущности общего подхода, ограничимся уравнением
 ,
,
где правая часть есть квадратичная форма, заданная в декартовой системе координат  . С другой стороны, это выражение определяет линию второго порядка. Ясно что если правая часть последнего равенства представлена суммой квадратов переменных
. С другой стороны, это выражение определяет линию второго порядка. Ясно что если правая часть последнего равенства представлена суммой квадратов переменных
 ,
,
то имеем канонический вид квадратичной формы.
Оба уравнения будут описывать одну и ту же линию второго порядка, если в форме h сохранен прежний масштаб. Для получения канонического вида H обычно используют характеристическое уравнение. Недостаток такого подхода состоит в том, что неизвестна связь между системами координат  и
и  . Образно говоря, мы не знаем расположение линии L в системе координат
. Образно говоря, мы не знаем расположение линии L в системе координат  , если она записана в каноническом виде h. Такой переход можно осуществить поворотом осей системы координат на угол j (рис. VII.1), то есть перейти от координат x, y к x 1, y 1 по формулам
, если она записана в каноническом виде h. Такой переход можно осуществить поворотом осей системы координат на угол j (рис. VII.1), то есть перейти от координат x, y к x 1, y 1 по формулам
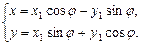

Рис. VII.1
Для обратного преобразования необходимо заменить угол j
на - j.
Чтобы узнать расположение линии, мы должны найти преобразование координат, приводящее равенство H к виду h. Заметим, что для сохранения масштаба следует перейти к ортонормированной системе координат.
Пример VII.5. Задана квадратичная форма в декартовой системе координат 
 . (VII.7)
. (VII.7)
Требуется привести ее к каноническому виду, то есть записать ее вид в системе  и найти линейное преобразование. Получить нормальный вид квадратичной формы.
и найти линейное преобразование. Получить нормальный вид квадратичной формы.
Решение. Составим симметричную матрицу линейного преобразования (оператора) A
 .
.
Построим характеристический многочлен и найдем собственные числа и собственные векторы. Затем будем последовательно выполнять задания примера. Имеем

Характеристическое уравнение представляется равенством
 .
.
Вычислив определитель матрицы, получим многочлен  , корни которого
, корни которого 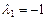 ,
,  являются собственными числами. Запишем канонический вид формы (VII.7):
являются собственными числами. Запишем канонический вид формы (VII.7):
 .
.
Найдем линейное преобразование, то есть установим связь между системами  и
и  . Так как корни действительные и различные и нет нулей, то преобразование невырожденное. Найдем собственные векторы
. Так как корни действительные и различные и нет нулей, то преобразование невырожденное. Найдем собственные векторы  в базисе
в базисе  (векторы будем представлять столбцами). Для этого решим систему уравнений
(векторы будем представлять столбцами). Для этого решим систему уравнений
 , (VII.8)
, (VII.8)
определенную для каждого из собственных чисел.
При 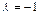 , из (VII.8) имеем матричное уравнение
, из (VII.8) имеем матричное уравнение
 .
.
Полагая, с необходимостью,  , получим
, получим
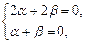
при 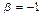 , имеем
, имеем  . Первый собственный вектор найден
. Первый собственный вектор найден 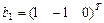 , его длина
, его длина  .
.
При  имеем
имеем
 или
или 
Прибавляя к первому уравнению второе и, замечая, что если полученное уравнение решать как систему с третьим, то с необходимостью перейдем к первому собственному вектору. Остается составить систему уравнений из суммы двух первых и второго уравнения, тогда получим

Полагая  , после упрощений получим систему
, после упрощений получим систему

из которой определяем  ,
,  . Второй собственный вектор найден:
. Второй собственный вектор найден:
 ,
,  .
.
При  , выполняя аналогичные действия, при
, выполняя аналогичные действия, при  получим третий собственный вектор
получим третий собственный вектор
 ,
, 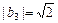 .
.
Для составления ортонормированной матрицы преобразования нормируем векторы  . Получаем ортонормированную матрицу оператора A, которая состоит из вектор-столбцов с нормирующим множителем
. Получаем ортонормированную матрицу оператора A, которая состоит из вектор-столбцов с нормирующим множителем  . Таким образом, матрица невырожденного линейного преобразования имеет вид
. Таким образом, матрица невырожденного линейного преобразования имеет вид
 .
.
Для записи линейного преобразования воспользуемся формулой  , из которой имеем
, из которой имеем

Подставляя вместо 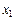 ,
,  ,
,  их правые части в перноначальную квадратичную форму f, получим ее канонический вид.
их правые части в перноначальную квадратичную форму f, получим ее канонический вид.
Можно также применить скалярное произведение для получения канонического вида квадратичной формы, если воспользоватьься формулой

 .
.
Все остальные слагаемые являются произведениями ортогоналных векторов, и потому их скалярное произведение равно 0.
Нормальный вид квадратичной формы получим из канонического вида заменой  ,
,  ,
, 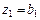 , тогда
, тогда 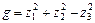 .
.