Продолжим изучение линейных операторов. Нам уже известно, что с каждым оператором A связана квадратная матрица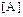 
, с которой, в свою очередь, связан ее определитель 
. Значение определителя есть скаляр (число). Следовательно, является функцией, ставящей в соответствие оператору A скаляр. Поэтому изучение свойств определителя может упростить исследование свойств оператора.
Определение. Скаляр l называется собственным числом (собственным значением), а ненулевой вектор x – собственным вектором линейного оператора A, действующего в n -мерном векторном пространстве L, если
. (VI.5)
Рассматривая 
как вектор 
, любой вектор 
, 
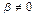, коллинеарный x, будет собственным вектором с собственным числом l. Если собственному значению l соответствует два вектора, x и y, то собственным вектором будет и любой ненулевой вектор вида 
. Поскольку 0-вектор не является собственным, то множество M всех собственных векторов оператора A не является подпространством. Если же M дополнить 0-вектором, то M станет подпространством. Кратностью собственного значения l называется размерность подпространства M; собственное значение l называется простым, если его кратность равна 1.
Упражнение. Найти все собственные числа и векторы операторов нулевого - О и тождественного – E. Определить их кратность, если линейный оператор действует в n -мерном линейном пространстве.
Теорема VI.1. Семейство собственных векторов 
оператора A, соответствующих аналогичному семейству собственных значений 
, 
, линейно независимо.
Доказательство. Применим метод математической индукции. При 
теорема верна по определению собственного вектора, как отличного от нулевого.
Пусть при любом 
, например, при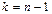 
, теорема верна, но неверна при 
. Тогда, если система векторов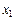 
, 
, …, 
, 
будет линейно зависимой, то есть существуют числа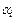 
, , не все равные 0, например, 
, что выполняется
. (VI.6)
Применяя к ней линейный оператор A, с учетом (VI.5), получим,
. (VI.7)
Умножая (VI.6) на 
и вычитая из (VI.7), будем иметь
.
Полученная линейная комбинация в силу индуктивного предположения линейно независима, то есть все коэффициенты при 
равны 0, в том числе и 
,но, по предположению, , тогда 
, но тогда 
, что невозможно, по условию теоремы. ▼
Следствие. Линейный оператор, действующий в n -мерном линейном пространстве, не может иметь более чем n попарно различных собственных значений.
Из определения собственного вектора линейного оператора следует, что образ и прообраз x – коллинеарны. Это означает, что не каждый линейный оператор, действующий в линейном пространстве над полем действительных чисел, имеет хотя бы один собственный вектор. Например, при любом повороте осей на угол, не кратный p, мы не получим коллинеарных векторов.
Перейдем к выводу уравнения, которому удовлетворяют все собственные векторы.
Пусть линейный оператор действует в n -мерном действительном линейном пространстве L и пусть , , некоторый базис, наконец 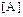– матрица оператора A в этом базисе. Линейный оператор 
является вырожденным тогда и только тогда, когда будет вырождена его матрица 
, то есть 
. Отсюда заключаем, что кратность l совпадает с дефектом линейного оператора .
Заметим, что, если B любой обратимый оператор, то можно показать [11], что
,
то есть 
тогда и только тогда, когда 
, где 
. Это означает, что все спектральные понятия (спектр, собственные значения, кратность, размерность и т.д.) инвариантны относительно замены A на подобный оператор 
. Учитывая что, по определению, определитель – это многочлен своих элементов, получаем
,
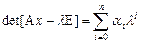где коэффициенты 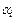являются функциями элементов определителя (или матрицы) и не зависят от l. Максимальная степень l входит лишь в один член определителя, составленного из произведения его элементов, стоящих на главной диагонали, поэтому 
. Таким образом, получаем многочлен
Раскрывая определитель, имеем
,
который называется характеристическим многочленом оператора A в вещественном линейном пространстве L.
Для того, чтобы число 
было собственным значением оператора A необходимо и достаточно, чтобы оно удовлетворяло уравнению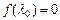 
, то есть, было бы корнем характеристического многочлена.
Пример VI.6. Является ли совпадение характеристических многочленов признаком равенства операторов?
Решение. Нет, не является, поскольку характеристический многочлен один и тот же для семейства подобных матриц. В самом деле, линейные операторы совпадают, если совпадают их матрицы. Рассмотрим два базиса и 
. Пусть оператор A, имеет в базисе матрицу 
, а в базисе – 
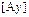. Тогда эти матрицы подобны, то есть 
, где Q – некоторая невырожденная матрица. Для любого 
, учитывая, что 
, имеем
.
Переходя к определителям матриц, получаем характеристический многочлен. То есть линейный оператор определяется характеристическим многочленом с точностью до подобия матриц.
Благодаря определителям задача нахождения собственных значений свелась к задаче алгебраической. В области действительных чисел не всякий многочлен степени 
имеет хотя бы один действительный корень. В то же время в области комплексных чисел, как следует из основной теоремы алгебры, любой многочлен имеет хотя бы один комплексный корень и, тем самым, n корней, пусть даже кратных. Этим объясняется большое значение комплексных линейных пространств.
Задача. Показать, что множество многочленов образует коммутативное кольцо (достаточно выполнения аксиом кольца).