Понятия поверхности и линии (кривой) относятся к фундаментальным понятиям геометрии (топологии); используются практически во всех математических и естественных науках. Поэтому их общее определение довольно затруднительно. В геометрии, аналитической и алгебраической, поверхность и линия определяются как геометрическое место точек, координаты которых записаны в декартовых координатах и удовлетворят уравнению 
или 
, соответственно.
В n -мерных линейных пространствах плоскость размерности (n -1) называется гиперплоскостью, а плоскость размерности 1 – прямой линией. Аналогичную терминологию будем применять и к поверхностям. Учитывая геометричность многих свойств поверхности и гиперповерхности, в дальнейшем будем называть векторы точками пространства действительных чисел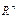 
. Это подтверждается и эквивалентностью понятий n -мерного векторного пространства и пространства 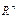[4].
Зададим в пространстве 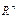декартовую систему координат и превратим его в евклидово, то есть определим в 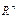скалярное произведение.
Определение. Гиперповерхностью f второго порядка в 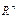называется множество точек 
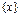, координаты 
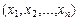которых удовлетворяют уравнению
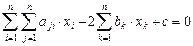, (VIII.1)
, 
.
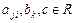Формулу (VIII.1) можно упростить, если определить скалярное произведение в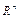 
как сумму попарных произведений координат, тогда получим
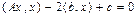. (VIII.2)
Учитывая симметричность матрицы A линейного оператора, имеем также для (VIII.1)
.
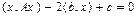Для исследования гиперповерхности (VIII.1) удобно преобразовать ее к каноническому виду. Воспользуемся уравнением (VIII.2). Процесс приведения к каноническому виду происходит в полном соответствии с алгоритмом приведения к каноническому виду квадратичных форм [7], которые нами уже изучены.
|
|
Классификация линий второго порядка
I. Рассмотрим в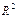 
гиперповерхность 2-го порядка, которая по определению имеет размерность 
, то есть является линией 2-го порядка.
Определение. Линией 2-го порядка в декартовой системе координат Oxy пространства 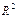называется множество точек, удовлетворяющих уравнению вида:
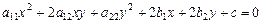. (VIII.3)
Применяя линейный оператор (преобразование) к уравнению (VIII.3), приводим его к одному из трех линейно независимых уравнений канонического вида:
1) 
,
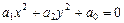2) 
, (VIII.4)
3) 
,
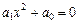где коэффициенты во всех уравнениях не равны нулю.
В зависимости от знака коэффициентов, выделим два класса линий [4]
· нераспадающиеся линии:
- эллипс;
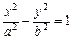- гипербола;
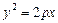- парабола;
· распадающиеся линии:
- пара мнимых пересекающихся прямых;
- пара действительных пересекающихся прямых;
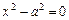- пара действительных параллельных прямых;
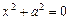- пара мнимых параллельных прямых;
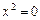- пара совпадающих действительных прямых.
Более подробно рассмотрим класс нераспадающихся линий.
Окружность
Окружностью называется геометрическое место точек плоскости, равноудаленных от некоторой фиксированной точки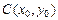 
, называемой ее центром.
Пусть точка 
произвольна и лежит на данной окружности, тогда расстояние СМ равно некоторому числу R, называемому радиусом этой окружности. В фиксированной системе координат уравнение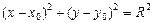 
определяет окружность с центром в точке 
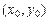и радиусом R.
Пример VIII.1. Найти центр и радиус окружности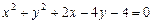 
.
Решение. Выделим полный квадрат по каждой переменной,
тогда уравнение можно записать в виде:
, или 
. Значит, это окружность с центром в точке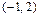 
и радиусом 
.
|
|
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Выведем уравнение эллипса. Пусть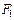 
и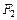 
– фокусы (рис. VIII.1). Положим 
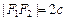. Декартову систему координат зададим следующим образом: ось Ox направим по прямой 
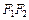, а начало поместим в середину отрезка 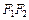. Тогда 
, 
.
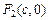Пусть – произвольная точка эллипса. Тогда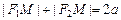 
, где величина a дана, причем 
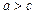. Имеем:
, 
.
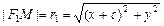И, следовательно, уравнение эллипса имеет вид:
.
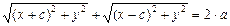Упростим последнее равенство: перенесем второе слагаемое последнего равенства в правую часть и возведем обе части
в квадрат, получим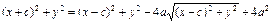 
,
выполним преобразования и приведем подобные: 
.
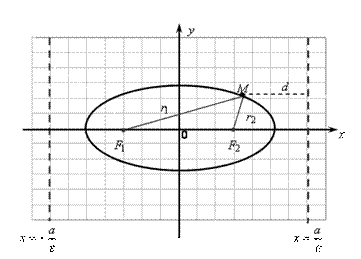
Рис. VIII.1
Разделим полученное равенство на четыре и возведем обе части еще раз в квадрат: 
, преобразуем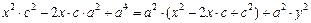 
, окончательно получим: 
, 
.
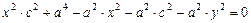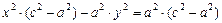Так как 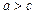, то обозначим 
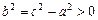и разделим обе части последнего равенства на эту величину: 
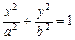– каноническое уравнение эллипса с полуосями 
, 
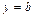и центром симметрии в точке 
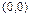. Число a в уравнении эллипса называется большой, а b – малой полуосью эллипса. Прямую, на которой расположены фокусы эллипса, называют фокальной осью.
Величина 
называется эксцентриситетом эллипса, а прямые 
называются директрисами эллипса.
Пример VIII.2. Доказать, что уравнение 
определяет эллипс.
Решение. Преобразуем данное уравнение, выделив полные квадраты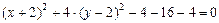 
. Введем новые переменные 
, 
. Тогда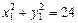 
или 
. Последнее уравнение определяет эллипс с центром в точке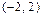 
, причем 
, 
.
|
|
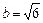Гипербола
Гиперболой называется геометрическое множество точек плоскости, для которых абсолютная величина разности расстояний до двух данных точек 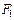и 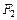этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Выведем уравнение гиперболы. Положим 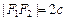. Систему координат (рис. VIII.2) выберем так же, как и в случае эллипса. Тогда , а 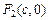. Если – произвольная точка гиперболы, то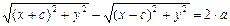 
, a – постоянная, 
. Это уравнение соответствует определению гиперболы. Преобразуя его, как и в случае эллипса, и положив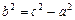 
, получим каноническое уравнение гиперболы:
.
Гипербола – кривая, симметричная относительно осей и начала координат. Прямые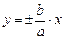 
являются асимптотами гиперболы, величина 
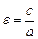называется эксцентриситетом гиперболы, 
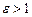, а прямые 
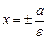– ее директрисами.
Рис. VIII.2
Парабола
Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F и данной прямой (рис. VIII.3). Точка F называется фокусом параболы, а данная прямая – директрисой параболы. Для получения уравнения параболы выберем систему координат следующим образом: ось Ox проведем через фокус F перпендикулярно директрисе. Начало координат поместим в точку, равноудаленную от фокуса и директрисы. Обозначим расстояние между фокусом и директрисой через p. Величина p называется параметром параболы. В выбранной системе координат фокус F имеет координаты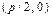 
, а уравнение директрисы имеет вид 
или 
, по определению 
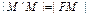
Рис. VIII.3
Пусть – произвольная точка параболы. Соединим точку М с точкой F. Проведем отрезок MM' перпендикулярно директрисе. Согласно определению параболы 
. По формуле расстояния между двумя точками находим: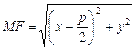 
, а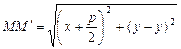 
. Следовательно, 
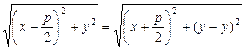. После элементарных преобразований получим каноническое уравнение параболы:
.
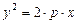Пример VIII.3. Классифицировать линию 2-го порядка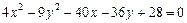 
.
Решение. Воспользуемся формулой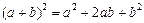 
. Выделим полный квадрат по каждой переменной, для этого сгруппируем отдельно слагаемые, содержащие переменную x и y: 
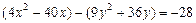. Коэффициенты при переменных в старшей степени вынесем общими множителями 
. Полученные выражения в скобках дополним до полного квадрата, в первом случае прибавим и отнимем 25, во втором – 4: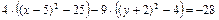 
. После раскрытия скобок постоянные перенесем в правую часть равенства 
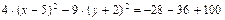. Приведем подобные 
. Запишем уравнение линии 2-го порядка в общем виде. Разделим последнее равенство на 36, чтобы получить единицу в правой части
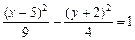или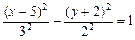 
.
Данная линия (рис. VIII.4) является гиперболой с центром в точке 
и полуосями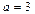 
, 
.
Рис. VIII.4