II. Рассмотрим в 
поверхность 2-го порядка, которая имеет размерность 
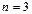[9, 10].
Определение. Поверхностью 2-го порядка в декартовой системе координат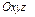 
пространства называется множество точек, удовлетворяющих уравнению вида
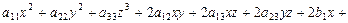
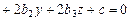. (VIII.5)
Линейным преобразованием (матрицей линейного оператора) уравнение (VIII.5) приводится к одному из пяти линейно независимых уравнения канонического вида
1) 
,
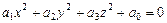2) 
,
3) 
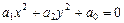, (VIII.6)
4) 
,
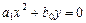5) 
,
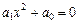где коэффициенты во всех уравнениях не равны 0.
Как и ранее, выделим классы поверхностей:
· невырожденные и нераспадающиеся поверхности:
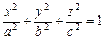- эллипсоид (рис. VIII.5);
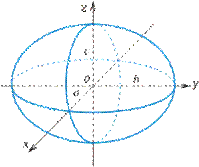
Рис. VIII.5
Если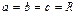 
, то эллипсоид становится сферой
(рис. VIII.6);
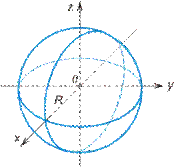
Рис. VIII.6
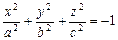- мнимый эллипсоид;
- однополостной гиперболоид (рис. VIII.7);
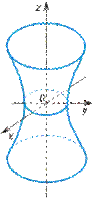
Рис. VIII.7
- двуполостной гиперболоид (рис. VIII.8);
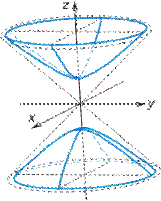
Рис. VIII.8
, 
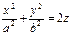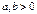- эллиптический параболоид (рис. VIII.9);
Рис. VIII.9
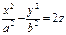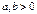, - гиперболический параболоид (рис. VIII.10);
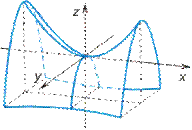
Рис. VIII.10
· вырождающиеся нераспадающиеся поверхности:
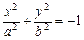- мнимый эллиптический цилиндр;
- эллиптический цилиндр (рис. VIII.11);
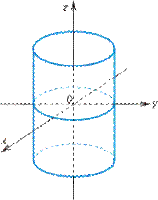
Рис. VIII.11
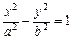- гиперболический цилиндр (рис. VIII.12);
Рис. VIII.12
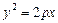- параболический цилиндр (рис. VIII.13);
Рис. VIII.13
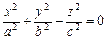- коническая поверхность (рис. VIII.14);
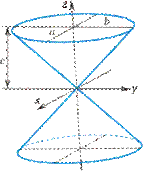
Рис. VIII.14
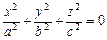- мнимая коническая поверхность;
· вырождающиеся распадающиеся поверхности:
- пара мнимых пересекающихся плоскостей;
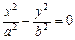- пара пересекающихся прямых;
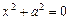- пара мнимых параллельных плоскостей;
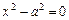- пара параллельных плоскостей;
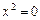- пара совпадающих плоскостей.
Пример VIII.4. Преобразовать к каноническому виду поверхность 2-го порядка
.
Решение. Прежде чем переходить к повороту осей координат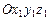 
, осуществим линейный перенос так, чтобы можно было применить методику квадратичных форм. Положим
, 
, 
,
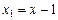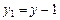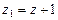тогда поверхность запишется в виде
.
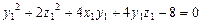Рассмотрим квадратичную форму
.
Составим матрицу квадратичной формы
.
Найдем собственные числа и собственные векторы. Имеем характеристический многочлен:
,
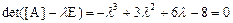корни которого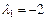 
, 
, 
.
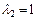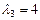Запишем канонический вид поверхности с точностью до коэффициентов (сначала запишем их положительные значения):
.
По классификации это однополостной гиперболоид. Явный вид линейного преобразования находим аналогично примерам предыдущего раздела:
,
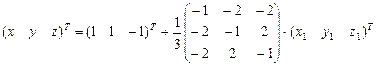где первое слагаемое определяет параллельный сдвиг, а второе поворот вокруг оси симметрии. Окончательно
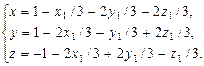
ЗАКЛЮЧЕНИЕ
Если вы читаете эту страницу, то будем считать, что знакомство с линейной алгеброй и с сопутствующими ей разделами математики состоялось. Конечно, для систематического применения на практике полученных знаний недостаточно. Существует много книг, способных расширить ваш кругозор. Однако особенностью развития современного научного общества является использование быстродействующих вычислительных средств, в основе которых лежит принцип параллельной обработки информации. Именно поэтому для углубленного изучения и применения методов и не только, линейной алгебры, в теории и практике, необходимо хорошее знание теории линейных операторов (преобразований) и алгоритмов (algorithm).
Одной из лучших книг для самообразования является фундаментальный труд: Кормен, Т.Х. Алгоритмы: построение и анализ / Т.Х. Кормен, Ч.И. Лейзерсон, Р.Л. Ривест, К. Штайн. – М.: Издательский дом «Вильямс», 2007. – 1296 с.
СПИСОК ЛИТЕРАТУРЫ
1. Александров, П.С. Курс аналитической геометрии и линейной алгебры / П.С. Александров. – СПб.; М.; Краснодар: Лань, 2009. – 512 с.
2. Ван дер Варден, Б.Л. Алгебра. Определения, теоремы, формулы / Б.Л. Ван дер Варден. – СПб.: Лань, 2004. – 624 с.
3. Воеводин, В.В. Линейная алгебра / В.В. Воеводин. – СПб.; М.; Краснодар: Лань, 2008. – 416 с.
4. Ильин, В.А. Аналитическая геометрия / В.А. Ильин, Э.Г. Позняк. – М.: Физматлит, 2008. – 280 с.
5. Кантор, И.Л. Гиперкомплексные числа / И.Л. Кантор, А.С. Солодовников. – М.: Наука, 1973. – 145 с.
6. Куратовский, К. Теория множеств / К. Куратовский,
А. Мостовский. – М.: Мир, 1970. – 416 с.
7. Курош, А.Г. Курс высшей алгебры / А.Г. Курош. – СПб.; М.; Краснодар: Лань, 2011. – 432 с.
8. Павский, В.А. Лекции по теории вероятностей и элементам математической статистики / В.А. Павский. – Кемерово: КемТИПП, 2005. – 184 с.
9. Постников, М.М. Теория Галуа / М.М. Постников.– М.: Факториал Пресс, 2003. – 304 с.
10. Френкель, А. Основания теории множеств / А. Френкель, И. Бар-Хиллел. – М.: Мир, 1966. – С. 556.
11. Халмош, П. Конечномерные векторные пространства / П. Халмош. – М., Ижевск: РХД, 2002. – 264 с.
12. Хайкин, С. Нейронные сети / С. Хайкин. – М.; СПб.; Киев: 2008. – 1003 с.
УЧЕБНОЕ ИЗДАНИЕ
Павский Валерий Аексеевич
ЛИНЕЙНАЯ АЛГЕБРА
Учебное пособие
Для студентов вузов
Редактор Т.В. Тулупова
Технический редактор Е.В. Кадочникова
Художественный редактор Е.П. Лопатин
ЛР № 020524 от 02.06.97
Подписано в печать 03.07.13. Формат 60×841/16
Бумага типографская. Гарнитура Times
Уч.-изд. л. 11,5. Тираж 150 экз.
Заказ № 9
Оригинал-макет изготовлен в лаборатории множительной техники
Кемеровского технологического института пищевой промышленности
650002, г. Кемерово, ул. Институтская, 7
ПЛД № 44-09 от 10.10.99
Отпечатано в лаборатории множительной техники
Кемеровского технологического института пищевой промышленности
650002, г. Кемерово, Институтская, 7