Рассмотри двухмерное евклидовое пространство ﻉ
с декартовой системой координат. Пусть точка 
ﻉ
и l Ìﻉ. Найдем расстояние от этой точки до прямой. Положим 
,и прямая l задается уравнением 
(рис. V.8).
Расстояние 
, вектор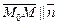 
, где 
– нормальный вектор прямой l, 
и 
– коллинеарны, поэтому их координаты пропорциональны, то есть 
, следовательно, 
, 
.
Рис. V.8
Отсюда 
или умножая эти уравнения
на A и B соответственно и складывая их, находим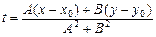 
, отсюда
или
.
Формула
(V.8)
определяет расстояние от точки 
до прямой .
Пример V.15. Найти уравнение прямой, проходящей через точку перпендикулярно прямой l: 
и найти расстояние от 
до прямой l.
Из рис. V.8 имеем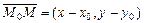 
, а нормальный вектор прямой l 
. Из условия перпендикулярности имеем
или
.
Так как 
, то
. (V.9)
Это и есть уравнение прямой, проходящей через точку , перпендикулярно прямой .
Пусть имеем уравнение прямой (V.9), проходящей через точку , перпендикулярна прямой l: . Найдем расстояние от точки до прямой l, используя формулу (V.8).
Для нахождения искомого расстояния достаточно найти уравнение прямой, проходящей через две точки и точку 
, лежащую на прямой в основании перпендикуляра. Пусть 
, тогда
. (V.10)
Так как 
, а вектор , то
. (V.11)
Поскольку точка лежит на прямой l, то имеем еще одно равенство 
или
Приведем систему к виду, удобному для применения метода Крамера
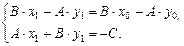
Ее решение имеет вид
,
. (V.12)
Подставляя (V.12) в (V.10), получаем исходное расстояние.
Пример V.16. В двухмерном пространстве задана точка 
и прямая 
. Найти расстояние от точки до прямой; записать уравнение прямой, проходящей через точку перпендикулярно заданной прямой и найти расстояние от точки до основания перпендикуляра к исходной прямой.
По формуле (V.8) имеем
.
Уравнение прямой, содержащей перпендикуляр, найдем как прямую, проходящую через две точки и , воспользовавшись формулой (V.11). Так как , то, с учетом того, что 
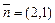, а 
, имеем
.
Для нахождения координат 
имеем систему с учетом того, что точка 
лежит на исходной прямой
Следовательно, 
, 
, отсюда 
.
Рассмотрим трехмерное евклидовое пространство ﻉ. Пусть точка ﻉ и плоскость PÌﻉ. Найдем расстояние от этой точки до плоскости P, заданной уравнением 
(рис. V.9).
Рис. V.9
Аналогично двухмерному пространству имеем и вектор 
, а 
, отсюда
. (V.13)
Уравнение прямой, содержащей перпендикуляр к плоскости P, запишем как уравнение прямой, проходящей через две точки и 
, лежащую в плоскости P:
. (V.14)
Для нахождения координат точки к двум любым равенствам формулы (V.14) добавим уравнение
. (V.15)
Решая систему трех уравнений (V.14), (V.15), найдем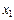 
, 
, 
– координаты точки . Тогда уравнение перпендикуляра запишется в виде
.
Для нахождения расстояния от точки до плоскости P вместо формулой (V.13) воспользуемся
.
Угол между прямой и плоскостью
Пусть заданы плоскость P и прямая l 
. Найдем угол между ними. Угол между прямой и плоскостью совпадает со смежным углом к углу образованным направляющим вектором 
прямой и нормальным вектором плоскости (рис. V.10). Так как 
, то
. (V.16)
Рис. V.10
Угол между плоскостями
Пусть даны две плоскости 
: 
и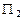 
: 
. Найдем угол между этими плоскостями, который совпадает с углом между их нормальными векторами 
и 
.
Учитывая, что
,
получим
. (V.17)
Пример V.17. Даны координаты вершин пирамиды 
, 
, 
, 
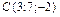. Найти: 1) длины ребер АВ и AC; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) объем пирамиды ABCD; 5) уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты пирамиды, опущенной на грань АВС. Сделать чертеж.
Решение.
1). Длина ребра AB совпадает с длиной вектора 
, поэтому определим координаты векторов и 
.
, 
.
Длина вектора равна корню квадратному из суммы квадратов его координат, то есть
, 
.
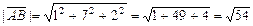2). Угол между ребрами AB и AC совпадает с углом между векторами и , который можно определить по формуле
, 
.
3). Грань ABC представляет собой треугольник, его площадь найдем через векторное произведение:
,
так как
.
4). Объем пирамиды вычислим по формуле:
.
Здесь 
.
5). Уравнение прямой, проходящей через точки А, В, имеет вид:
, то есть, 
.
6). Уравнение плоскости ABC определим из равенства
, 
или
.
7). Так как высота – это прямая перпендикулярная плоскости ABC, ее направляющим вектором будет вектор-нормаль 
плоскости ABC, тогда уравнение высоты имеет вид:
.
Выполним чертеж (рис. V.11).
Рис. V.11
VI. Линейные операторы
Линейный оператор
В линейной алгебре, помимо векторных пространств, фундаментальное значение имеют линейные операторы (или линейные преобразования) [1, 7, 11].
Как общее понятие, оператор – отображение одного множества на другое, каждое из которых наделено некоторой структурой (системой аксиом, отношением порядка, алгебраической операцией и т.д.). Аналогом оператора в математическом анализе является функция.
Современное определение линейного оператора A принадлежит Дж. Пеано для векторных пространств с основным полем R действительных чисел, с областью определения и областью значений в L.
Отметим, что при использовании современной вычислительной техники (кластеров, вычислительных систем, нейронных систем) эффективность параллельных программ существенно повышается, если представленные для решения задачи записаны в векторной (операторной) форме.
Поскольку линейный оператор рассматривается как отображение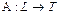 
, 
или как функция 
, то в дальнейшем, векторы будем обозначать малыми буквами x, y, …, возможно с индексами, 
.
Определение. Линейным оператором A на векторном пространстве L называется линейное преобразование одного вектора в другой из того же пространства, так что выполняются свойства линейности
,
, (VI.1)
что эквивалентно линейной комбинации,
, 
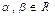. (VI.2)
Из (VI.1) следует, что среди линейных операторов существуют:
а) нулевой, 
, то есть такой, что 
, 
, где
0 – нулевой вектор;
б) единичный (тождественный) 
, то есть такой, что 
;
в) подобия P, то есть такой, что 
,
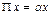отсюда следует, что при 
получаем нулевой оператор, а при 
тождественный.
Из (VI.2) следует, что 
, где 
, 
. Область значений оператора A является подпространством, в частности множество векторов 
, таких что 
– подпространство.
Множество 
называется ядром оператора A, а размерность ядра называется дефектом оператора A.
Пример VI.1. Пусть в векторном пространстве L задан базис. Оператор A ставит в соответствие каждому вектору x его координату с фиксированным номером. Доказать, что A – линейный оператор.
Доказательство. Пусть 
, 
, тогда, например, 
, 
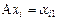, покажем, что
, 
.
В самом деле, имеем из (VI.2),
. ▼