Множество действительных чисел R линейно упорядочено, образует поле по отношению к арифметическим операциям, включает в себя множество рациональных чисел Q. Важным свойством действительных чисел является свойство непрерывности, понятие, основанное на признаке близости соседних элементов. Во множестве R получила развитие теория пределов, непрерывных функций, что привело к созданию дифференциального и интегрального исчисления. Множество R имеет кардинальное число 
~2æ0 – мощность континуума.
Из школьной математики известно, что десятичные дроби бывают конечные и бесконечные. Бесконечные дроби разделяют на периодические и непериодические. Любые рациональные числа, включая целые, представимы в виде периодической десятичной дроби. Существуют ли числа, представимые непериодическими десятичными дробями, то есть числа, не являющиеся рациональными? Это тем более важно, что в области рациональных чисел не определено решение уравнений, например,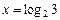 
или 
, 
. Такие числа существуют, и они не только представимы десятичной непериодической дробью, но и являются, по этой причине, решениями уравнений отмеченного класса. Эти числа назвали иррациональными (irrationalis – недоступные разуму, не существующие), и в совокупности с рациональными они образуют множество действительных чисел R, существенно расширяющих понятие числа.
Покажем, что на координатной (числовой) прямой можно поместить все действительные числа и других, более широкого множества чисел, там быть не может [3].
В самом деле, пусть имеем числовую прямую, то есть геометрическую прямую, на которой заданы начало, масштаб
и направление. Сечением прямой в любой ее точке (числе) p назовем ее представление в виде двух интервалов вида:
1) 
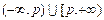; 2) 
, где 
. Воспользуемся одним из свойств, определяющих рациональное число: для любых 
, 
всегда содержится бесконечное число неравных рациональных чисел. Отсюда следует, что есть еще один вариант сечения числовой прямой: 3) 
, то есть существует нерациональное число, через которое проходит сечение. Таких чисел, очевидно, много больше, чем рациональных чисел. Объединяя их в одно множество, получим, что любое сечение числовой прямой проходит через действительное число, то есть имеем деление на два класса чисел, и других чисел нет. Именно поэтому числовую прямую называют множеством действительных (вещественных) чисел.
Построением теории действительных чисел занимались
Г. Кантор, Дедекинд (J.W.R. Dedekind, 1831-1916) и К. Вейерштрасс (K.T.W. Weierstras, 1815-1897). Рассмотренные здесь сечения называются сечениями Дедекинда.
Итак, множество действительных чисел R состоит из множества рациональных чисел Q и множества чисел, дополняющих рациональные числа до непрерывности, то есть иррациональных, обозначаемое как 
или 
.
В дальнейшем выяснилось, что действительные числа удобно разделить на два класса: алгебраические числа и все остальные, которые назвали трансцендентными.
Алгебраические – это числа, являющиеся корнями алгебраических уравнений n -ой степени вида 
, где 
, 
. Если 
, то корень уравнения, если он существует, называется целым алгебраическим числом (например, уравнение 
имеет корнем целое алгебраическое число 
, а уравнение 
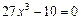имеет корнем просто алгебраическое число 
).
Ясно, что каждое рациональное число 
– алгебраическое, так как является решением уравнения 
.
Примерами трансцендентных чисел являются, например, число 
, число 
, число 
. Хотя трансцендентных чисел очень много, проверить на иррациональность заданное число очень трудно. Существуют числа, трансцендентность которых еще не выяснена.