Запишем выражение для дохода фирмы для случая рекламы услуг на примере услуг связи (все остальные случаи рассматриваются аналогично).
Доход, очевидно, будет состоять из двух частей.
- Одна из них связана с продажей товара (например, сотового телефона) или стоимостью подключения (разовый платеж), которая вычисляется по формуле (44). Отметим, что в некоторых случаях торговая наценка может быть отрицательной.
- Вторая часть дохода связана с внесением абонентской платы.
Пусть каждый вновь привлеченный фирмой абонент вносит ежемесячную абонентскую плату р*. Тогда доход от оплаты услуг запишется в виде:
I = p*NP,
(58)
где - N число платежей.
При вычислении числа платежей будем считать, что они осуществляются абонентами, пришедшими за время рекламного цикла (Т месяцев) в течение М месяцев после начала учета прихода абонентов.
Вначале предположим, что пришедшие абоненты не уходят. В этом случае число платежей вычисляется по формуле
Np= NFn(T,M).
(59)
Здесь NF = DLS + DBF - число пришедших абонентов,
функция n(Т,М) описывает число платежей за Т месяцев прихода (подключения) новых абонентов и за М месяцев сбора абонентской платы.
С. 90
Вычислим функцию n(Т,М). Принцип ее вычисления показан на рис. 29.
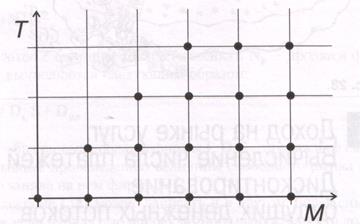
Рис. 29. Число платежей при Т = 4, М = 6.
Здесь изображена ситуация, в которой подключение новых абонентов продолжалось 4 месяца (Т=4), а время сбора абонентской платы составляло 6 месяцев (М=6) от начала подключения абонентов. В этом случае абонент,
- пришедший в первый месяц, вносит абонентскую плату 6 раз,
- пришедший во второй месяц - 5 раз,
- в третий - 4 раза,
- в четвертый - 3 раза.
Всего имеем 18 платежей (изображены точками). Суммируя эти точки для произвольных М и Т, получим следующую формулу для функции n(Т,М):
|
|
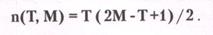
(60)
С. 91
На рис. 30 показана наглядная интерпретация формулы (60).
Рис. 30.
Теперь учтем уход (отключение) абонентов. Средний процент ухода абонентов за месяц обозначим 
. Нетрудно показать, что в этом случае формула (60) примет вид:
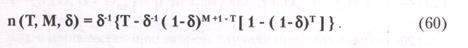
(60)
На рис. 31 приведена зависимость числа платежей от процента ухода абонентов в месяц. Кривые 1, 2 и 3 соответствуют одному, трем и шести месяцам прихода новых абонентов. При этом считалось, что сбор абонентской платы составлял 12 месяцев (М=12).
Если ухода абонентов нет, то число платежей в соответствии с (60) при этих условиях равно 12, 33 и 57 соответственно (см. точки кривых по оси ординат на рис. 31). При уходе абонентов удельное число платежей уменьшается, что и демонстрирует рис. 29.
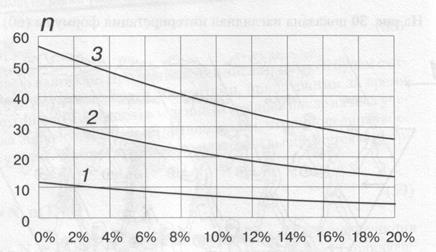
Рис. 31. Зависимость числа платежей от процента ухода абонентов.
Если рассматривать абонентские платежи, осуществляемые одним человеком, как денежный поток за большой промежуток времени, то можно ввести эквивалент торговой наценки. Известно, что стоимость будущих платежей отличается от современной стоимости платежа. Поэтому эквивалент торговой наценки в случае протяженных по времени платежей вычисляется введением стандартной процедуры ДИСКОНТИРОВАНИЯ БУДУЩИХ ДЕНЕЖНЫХ ПОТОКОВ.
Процедура дисконтирования приводит к эффективному уменьшению реальной стоимости будущей абонентской платы. Результат расчета приведен на рис. 32.
На этом рисунке показана зависимость суммарной эффективной абонентской платы (отнесенной к ее номинальному значению) от числа месяцев сбора абонентской платы М при разной месячной ставке дисконтирования
|
|
i = 0%,
i = 20% и
i = 40%.
При этом считалось, что
- число месяцев прихода новых абонентов Т = 1,
- и пришедшие абоненты не уходят - 
= 0%.
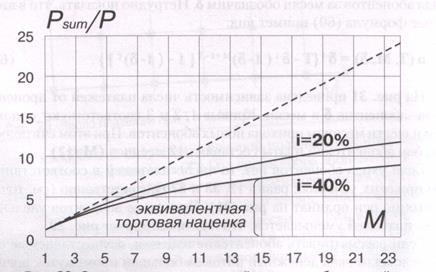
Рис. 32. Зависимость относительной величины абонентской платы от времени при разной ставке дисконтирования
С. 93 Из рисунка видно, что при нулевой ставке дисконтирования эффективная абонентская плата равна своему номинальному значению и суммарные платежи неограниченно возрастают со временем.
Однако при 20% и 40% месячной ставке дисконтирования суммарная эффективная абонентская плата с течением времени выходит на определенный предел роста. Таким образом, начиная с некоторого значения М (которое можно назвать временным горизонтом при заданной ставке дисконтирования) сумма абонентских платежей практически не меняется при увеличении времени.