СПЕКТР ОХВАТА НЕСКОЛЬКИХ СМИ G(F)

Нами была получена формула, по которой вычисляет­ся охват нескольких СМИ. Теперь, как и для одного СМИ, предста­вим этот полный охват G нескольких СМИ в виде разложения в спектр - то есть в виде суммы охватов g(f), соответствующих всем возможным числам контактов. Общая формула для L СМИ оказы­вается достаточно громоздкой. Поэтому мы проиллюстрируем вывод этого разложения на примере двух (L=2) независимых СМИ.

Пусть имеются два СМИ с охватами G1(m1) и G2(m2), где m1 и m2 - выходы в 1 и 2 СМИ. Охват двух СМИ в соответствии с формулой (17) будет следующим

(32)

Эту формулу наглядно иллюстрирует рис. 20, на котором охва­ты представлены в виде пересекающихся кругов.

- Пересеченная часть (область 2) представляет собой долю людей, имевших контакт как с первым, так и со вторым СМИ.

- Области 1 и 3 представляют собой доли людей, имевших контакт только с 1 и только со вторым СМИ соответственно.

- Полный охват равен сумме этих трех областей (объе­динение охватов двух СМИ).

Рис. 20. Схематическое представление охвата двух СМИ как суммы трех областей.

Определим охваты отдельных областей.

· Начнем с охвата совме­стного сектора 2.

Предположим, что контакты любого человека из целевой аудитории с этими двумя СМИ являются случайными. Ра­нее уже говорилось, что охват на языке теории вероятностей пред­ставляет собой вероятность того, что случайно выбранный из ауди­тории человек имел, по крайней мере, один контакт со СМИ.

Поэто­му G1(m1) и G2(m2) - вероятности контактов с первым и вторым СМИ. При случайных контактах со СМИ вероятность того, что случайно выбранный из аудитории человек имел контакт как с первым, так и со вторым СМИ, равна произведению вероятностей G1(m1) и G2(m2) (см. соответствующую теорему в [9]). Поэтому формулу (26) можно пе­реписать в виде суммы охватов областей 1, 3 и 2:

· Теперь представим полный охват двух СМИ G как сумму охватов с фиксированным числом контактов, используя разложение (18), (19) для первого и второго СМИ.

(34)

С. 72

Подставляя (34) в (33) и группируя от­дельные слагаемые так, чтобы каждая группа соответствовала фик­сированному числу контактов, получим следующее разложение для полного охвата:

Для большего числа СМИ формула для спектра охвата g (f) вы­водится аналогично. Однако из-за ее громоздкости мы ее здесь не при­водим.

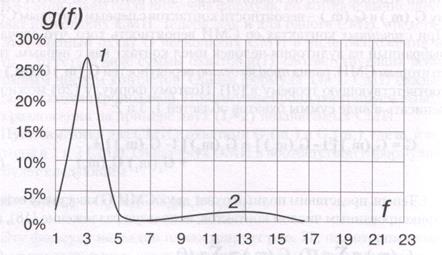
На рис. 21 показан спектр охвата g(f) двух СМИ (TV и радио), полученный по формуле (22). Параметры СМИ были следующи­ми:

1) для телепередачи - R=15%; m = 12;

2) для радиопередачи - R=5 %; m = 20.

С. 73

Из рисунка видно, что на кривой g(f) имеется 2 макси­мума. Эта кривая является суммой двух кривых, каждая из которых имеет один максимум и относится к одному СМИ.

Первый максимум охвата при частоте контакта f1 = 3 возникает благодаря выходам на TV.

Второй - на частоте f2 = 13 возникает в ре­зультате выходов на радио.

ВЫВОД:

Из этого рисунка видно, что относительно небольшое число выходов в рейтинговом СМИ позволяет охватить значительное число людей, но с небольшим числом контактов. В то же время достаточно большое число выходов в малорейтинговом СМИ обеспечивает большое число контактов, но конечно, меньший охват.

· Отметим, что для случая двух сильно рейтинговых СМИ

кривая g(f) может иметь и три максимума, которые соответствуют частотам

- f1,

- f2 и

- f1+ f2

где

f1= m1R1/G(m1),

f2 = m2R2/G(m2);

mj, Rj - выходы и рейтинги каждого СМИ.

В общем случае нескольких СМИ кривая g(f) может иметь 2` L -1 максимумов на разных частотах (L - число СМИ).

Однако, как пра­вило, число максимумов оказывается меньше за счет их слияния. При увеличении числа СМИ в результате такого слияния кривая g (f) ста­новится более гладкой и широкой.

ГРАФИК:

В качестве примера на рис. 22 приведено распределение охвата для трех СМИ (TV-передача, радио, пресса) с параметрами:

l) R=15%; m = 25;

2) R=6%; m = 20;

3) R=20%; m = 4.

С. 74

Для этого примера выходы были подобраны так, чтобы все три главных максимума были, по возможности, отделены друг от друга (всего максимумов для трех СМИ может оказаться 7).

Однако, как видно из сравнения рис. 21 и 22, при увеличении числа СМИ вклады каждого из них перекрываются (между макси­мумами нет участков кривой, где g(f) = 0). В результате общую кри­вую нельзя разделить на участки, каждый из которых отвечает только одному СМИ. Но каждый из трех четко выделенных максимумов на представленной кривой идентифицируются с одним из трех СМИ.