Постановка задачи.
Тебуется наути безусловный минимум функции f(x) одной переменной, т.е. такую точку  , что
, что 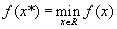 .
.
Стратегия поиска.
Метод относится к последовательным стратегиям и позволяет исключить из дальнейшего рассмотрения на каждой итерации ровно половину текущего интервала неопределенности. Задается начальный интервал неопределенности и требуемая точность.
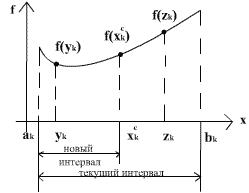
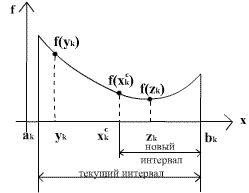
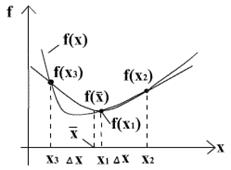
Алгоритм основан на анализе значений функции в трех точках, равномерно распределенных на текущем интервале (делящих его на четыре равные части). Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1. Задать начальный интервал неопределенности 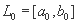 и требуемую точность
и требуемую точность  .
.
Шаг 2. Положить k=0.
Шаг 3. Вычислить среднюю точку  , длину интервала
, длину интервала 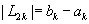 и значение функции в средней точке
и значение функции в средней точке  .
.
Шаг 4. Вычислить точки:  ,
,  , а также значения функции в этих точках:
, а также значения функции в этих точках: 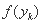 ,
, 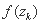
Шаг 5. Сравнить значения 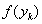 и
и 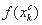 :
:
а) если 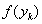 <
<  , исключить интервал
, исключить интервал 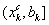 , положить
, положить 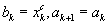 . Средней точкой нового интервала становится точка
. Средней точкой нового интервала становится точка  :
: 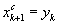 . Перейти к шагу 7.
. Перейти к шагу 7.
б) если 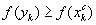 , перейти к шагу 6.
, перейти к шагу 6.
Шаг 6. Сравнить значения 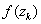 и
и  :
:
а) если 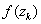 <
<  , исключить интервал
, исключить интервал 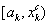 , положить
, положить 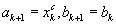 . Средней точкой нового интервала становится точка
. Средней точкой нового интервала становится точка 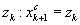 Перейти к шагу 7.
Перейти к шагу 7.
б) если 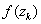

 , исключить интервалы:
, исключить интервалы:  , положить
, положить  . Средней точкой нового интервала остается точка
. Средней точкой нового интервала остается точка 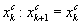 . Перейти к шагу 7.
. Перейти к шагу 7.

Шаг 7. 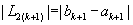 и проверить условие окончания:
и проверить условие окончания:
a) если  , процесс поиска заканчивается и
, процесс поиска заканчивается и 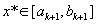 . В качестве приближения можно взять середину этого интервала
. В качестве приближения можно взять середину этого интервала  .
.
б) если 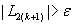 , то положить k=k+1 и перейти к шагу 4.
, то положить k=k+1 и перейти к шагу 4.
Сходимость.
Для метода дихотомии характеристика относительного уменьшения начального интервала неопределенности находится по формуле 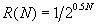 , где N - количество вычислений функции.
, где N - количество вычислений функции.
Ввиду медленной сходимости этот метод редко используется для нахождения значения корня, обычно его применяют для локализации корня с дальнейшим уточнением значения корня каким-либо другим методом.
Пример.
Задание. Определить методом дихотомии минимум функции 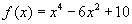 , заданной на отрезке
, заданной на отрезке 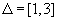 , при
, при 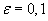 .
.
Решение.


Метод Золотого сечения.
Постановка задачи.
Тебуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку  , что
, что 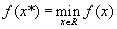 .
.
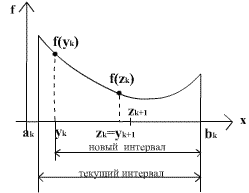
При построении конкретного метода одномерной оптимизации, работающего по принципу сокращения интервала неопределенности, следует определиться с правилом выбора на каждой итерации двух внутренних точек, при этом желательно, чтобы одна из них всегда использовалась в качестве внутренней для следующего интервала. В этом случае число вычислений функции сократится вдвое, и новая итерация потребует расчета только одного нового значения функции. В методе золотого сечения в качестве внутренних точек выбираются точки золотого сечения.
Определение. Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей.
Рассмотрим для простоты отрезок [0,1] единичной длины.
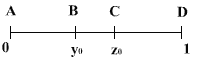
Ясно, что на отрезке имеется две таких точки  и
и 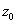 , они симметричны относительно концов. Точка
, они симметричны относительно концов. Точка  производит золотое сечение отрезка [A,C], а точка
производит золотое сечение отрезка [A,C], а точка 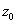 производит золотое сечение отрезка [BD]. Положим |AB|= x. Тогда |BD|=1-x. В соответствии с определением точки «золотого сечения» имеем:
производит золотое сечение отрезка [BD]. Положим |AB|= x. Тогда |BD|=1-x. В соответствии с определением точки «золотого сечения» имеем: 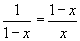 . Решив эту пропорцию, получим
. Решив эту пропорцию, получим  .
.
Стратегия поиска.
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм основан на анализе величин функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1. Задать начальный интервал неопределенности 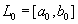 и требуемую точность
и требуемую точность  .
.
Шаг 2. Положить k=0.
Шаг 3. Вычислить точки  ,
, 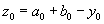 .
.
Шаг 4. вычислить значения: 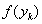 ,
, 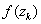
Шаг 5. Сравнить значения 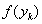 и
и 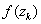 :
:
а) если 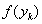
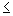
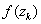 , исключить интервал
, исключить интервал 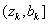 , положить
, положить
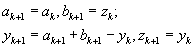 .
.
Перейти к шагу 6.

б) если 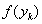 >
> 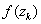 , то исключить интервал
, то исключить интервал 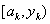 , положить
, положить
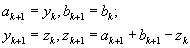 .
.
Перейти к шагу 6.
Шаг 6. Вычислить 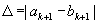
а) если 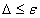 , то поиск завершен
, то поиск завершен 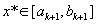 . В качестве приближения можно взять середину этого интервала
. В качестве приближения можно взять середину этого интервала  .
.
б) если  то положить k=k+1 и перейти к шагу 4.
то положить k=k+1 и перейти к шагу 4.
Сходимость.
Для метода золотого сечения характеристика относительного уменьшения начального интервала неопределенности находится по формуле  , где N - количество вычислений функции.
, где N - количество вычислений функции.
Пример.
Задание.
Определить методом Золотого сечения минимум функции  , заданной на отрезке
, заданной на отрезке  , при
, при  .
.
Решение.

Метод Фибоначчи.
Постановка задачи.
Тебуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку  , что
, что 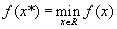 .
.
В методе Фибоначчи реализована стратегия, обеспечивающая максимальное гарантированное сокращение интервала неопределенности при заданном количестве вычислений функции. Эта стратегия опирается на числа Фибоначчи.
Определение. Числа Фибоначчи определяются следующим образом:
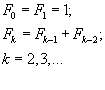 .
.
Последовательность чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,….
Стратегия поиска.
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и количество N вычислений функции. Алгоритм основан на анализе величин функции в двух точках. Точки вычисления функции находятся с использованием последовательности из N+1 чисел Фибоначчи. Как и в методе золотого сечения, на первой итерации требуется два вычисления функции, а на каждой последующей итерации, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1. Задать начальный интервал неопределенности 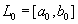 , ], допустимую длину конечного интервала l > 0 и константу различимости
, ], допустимую длину конечного интервала l > 0 и константу различимости  .
.
Шаг 2. Найти количество N вячислений функции как наименьшее целое число, при котором удовлетворяется условие 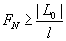 , и числа Фибоначчи
, и числа Фибоначчи  .
.
Шаг 3. Положить k=0.
Шаг 4. Вычислить значения:
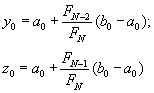 .
.
Шаг 5. Вычислить 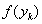 ,
, 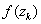 .
.
Шаг 6. Сравнить 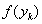 с
с 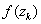
а) если 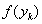
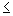
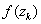 , положить
, положить
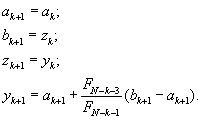
Перейти к шагу 7;
б) если 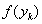 >
> 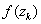 , положить
, положить
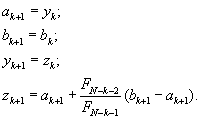 .
.
Шаг 7. Проверить условие окончания и в случае необходимости сделать заключительное N-е вычисление функции для получения решения:
а) если 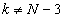 , положить k=k+1 и перейти к шагу 5;
, положить k=k+1 и перейти к шагу 5;
б) если k=N-3, то всегда 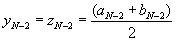 , т.е. отсутствует точка нового вычисления функции. В этом случае полагают:
, т.е. отсутствует точка нового вычисления функции. В этом случае полагают:  . В точках
. В точках 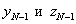 вычисляют значения функции и находят границы конечного интервала неопределенности:
вычисляют значения функции и находят границы конечного интервала неопределенности:
o Если  , положить
, положить 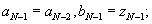
o Если 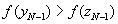 , положить
, положить 
Поиск завершен и 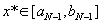 . В качестве приближения можно взять середину этого интервала
. В качестве приближения можно взять середину этого интервала 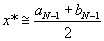 .
.
Сходимость.
Для метода Фибоначчи характеристика относительного уменьшения начального интервала неопределенности находится по формуле 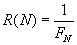 , где N - количество вычислений функции.
, где N - количество вычислений функции.
Пример.
Задание.
Определить методом Фибоначчи минимум функции  , заданной на отрезке
, заданной на отрезке  , при
, при 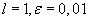 .
.
Решение.

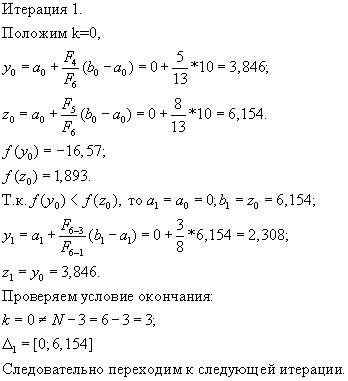


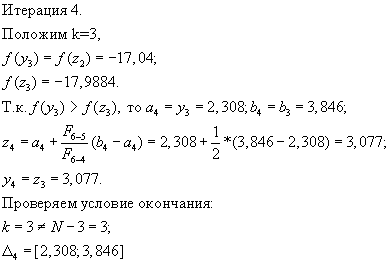

Метод Пауэлла.
Основная идея методов полиномиальной аппроксимации связана с возможностью аппроксимации гладкой функции полиномом и последующего использования аппроксимирующего полинома для оценивания координаты точки оптимума. Необходимыми условиями эффективной реализации такого подхода являются унимодальность и непрерывность исследуемой функции.
Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома.
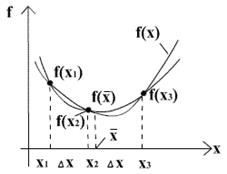
Простейшим вариантом полиномиальной аппроксимации является квадратичная аппроксимация, которая основана на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть, по крайней мере, квадратичной. Если же функция линейная, то ее оптимальное значение может достигаться только в одной из двух граничных точек интервала. Таким образом, при реализации метода оценивания с использованием квадратичной аппроксимации предполагается, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, а затем использовать построенный полином для оценивания координаты точки истинного минимума функции.
Пусть известны значения функции f(x) в трех разных точках 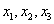 , равные соответственно
, равные соответственно  , тогда функция f(x) может быть аппроксимирована квадратичной функцией:
, тогда функция f(x) может быть аппроксимирована квадратичной функцией: 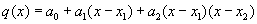 , где коэффициенты
, где коэффициенты 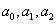 определяются из условия, что значения функции в этих точках равны значениям полинома q(x) в этих же точках.
определяются из условия, что значения функции в этих точках равны значениям полинома q(x) в этих же точках.
Имеем

Отсюда получаем
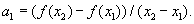
Аналогично получаем 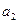 :
:
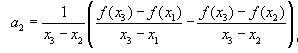
Квадратичная функция q(x) достигает минимума в точке 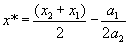 .
.
Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина 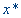 окажется приемлемой оценкой координаты точки истинного оптимума функции f(x).
окажется приемлемой оценкой координаты точки истинного оптимума функции f(x).
Стратегия поиска.
Метод Пауэлла относится к последовательным стратегиям. Задается начальная точка и с помощью пробного шага находится три точки так, чтобы они были как можно ближе к искомой точке минимума. В полученных точках вычисляются значения функции. Затем строится интерполяционный полином второй степени, проходящий через эти точки. В качестве приближения точки минимума берется точка минимума полинома. Поиск заканчивается, когда полученная точка отличается от лучшей из трех опорных точек не более чем на заданную величину.
Алгоритм.
Шаг 1. Задать начальную точку  , величину шага
, величину шага 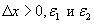 - малые положительные числа, характеризующие точность.
- малые положительные числа, характеризующие точность.
Шаг 2. 
Шаг 3. Вычислить 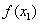 и
и 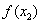 .
.
Шаг 4. Сравнить 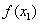 и
и 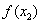 :
:
o Если 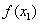 >
> 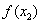 , то
, то  .
.
o Если 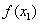 <
< 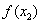 , то
, то  .
.
Шаг 5. Вычислить  и найти
и найти 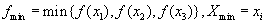 :
: 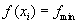 Шаг 6. По
Шаг 6. По 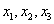 вычислить
вычислить  , используя формулу для оценивания с помощью квадратичной аппроксимации:
, используя формулу для оценивания с помощью квадратичной аппроксимации:
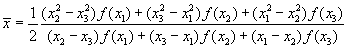 и значение функции
и значение функции  .
.
Если знаменатель в формуле для  на некоторой итерации обращается в нуль, то в этом случае результатом интерполяции является прямая, тогда следует положить
на некоторой итерации обращается в нуль, то в этом случае результатом интерполяции является прямая, тогда следует положить 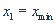 и перейти к шагу 2.
и перейти к шагу 2.
Шаг 7. Проверка окончания:

a) если оба условия выполнены, процедура закончена и 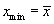 ;
;
б) если хотя одно из условий не выполнено и  , выбрать наилучшую точку (
, выбрать наилучшую точку ( или
или 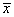 ) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 5.
) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 5.
в) если хотя одно из условий не выполнено и 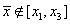 , то положить
, то положить 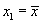 и перейти к шагу 2.
и перейти к шагу 2.
Пример.
Задание.
Определить методом Пауэлла минимум функции 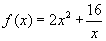 в интервале
в интервале 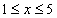 .
.
Решение.


Метод секущих.
Стратегия поиска.
Метод секущих ориентирован на нахождение корня уравнения f(x)=0 в интервале [a,b], в котором имеются две точки, в которых f(a), f(b) < 0. Между этими точками проводится секущая к кривой y= f(x). В качестве следующего приближения выбирается точка пересечения этой секущей с осью абсцисс. Процесс построения секущих и нахождения точек пересечения с осью продолжается до тех пор, пока разность между двумя последовательными приближения не станет меньше  .
.
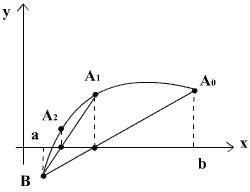
Геометрически этот способ эквивалентен замене кривой f(x) секущей 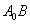 , проходящей через
, проходящей через 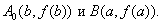
Точка пересечения  секущей
секущей 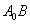 с осью Ox Ох может быть найдена из уравнения:
с осью Ox Ох может быть найдена из уравнения:

Полагая у = 0, имеем:
 .
.  ищем как пересечение секущей
ищем как пересечение секущей 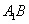 , где
, где 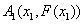 , с осью Ox:
, с осью Ox:
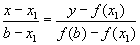 ,
,
Полагая опять y=0, имеем:
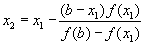
и т.д.
Каждое очередное приближение к стационарной точке  определяется по формуле:
определяется по формуле:
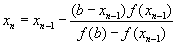
Процесс продолжается до тех пор, пока не выполнится условие окончания поиска:

Примерное количество итераций n, необходимое для вычисления корня с относительной точностью  ,определяется неравенством:
,определяется неравенством:
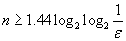
Алгоритм.
Шаг 1. На отрезке [a,b] задать начальное приближение  и точность вычисления
и точность вычисления  .
.
Шаг 2. Вычислить очередное приближение по формуле:
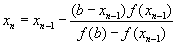 , где n=1,2,...
, где n=1,2,...
Шаг 3. Повторить процедуру 2 до тех пор, пока  , тогда
, тогда 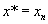 .
.
Пример.
Задание.
Найти минимум функции 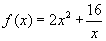 на интервале 1<X
на интервале 1<X  .
.
Решение.
