Все численные методы одномерной безусловной оптимизации условно можно сгруппировать следующим образом:
1. Методы исключения интервалов (линейный поиск):
1.1. Метод половинного деления;
1.2. Метод «золотого сечения»;
1.3. Метод Фибоначчи;
2. Метод полиномиальной аппроксимации:
2.1. Метод Пауэлла;
3. Методы с использованием производных:
3.1. Метод секущих;
3.2. Метод качательных.
Первые две группы методов используют только значения функции и не требуют вычисления ее производных и называются методами минимизации нулевого порядка.
Методы исключения интервалов накладывают единственное требование на исследуемую функцию: она должна быть унимодальной. Следовательно, указанные методы можно использовать для анализа как непрерывных, так и разрывных функций, а также в случаях, когда переменные принимают значения из дискретного множества. Логическая структура поиска с помощью методов исключения интервалов основана на простом сравнении значений функции в двух пробных точках. Кроме того, при таком сравнении в расчет принимается только отношение порядка на множестве значений функции и не учитывается величина разности между значениями функции.Большим достоинством этих методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы методов нулевого порядка, это возможность определения значений f(x) в заданных точках, а также, что исследуемая целевая функция в допустимой облас-ти, по крайней мере, обладает свойством унимодальности.
Определение 3. Функция f(x) называется унимодальной, если существует такая точка x*, что из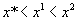 
следует 
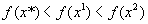, а из 
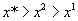следует 
.
Другими словами, слева от x* функция f(x) монотонно убывает, а справа - монотонно возрастает.
Отметим, что в данном определении не предполагается ни гладкость, ни непрерывность функции.
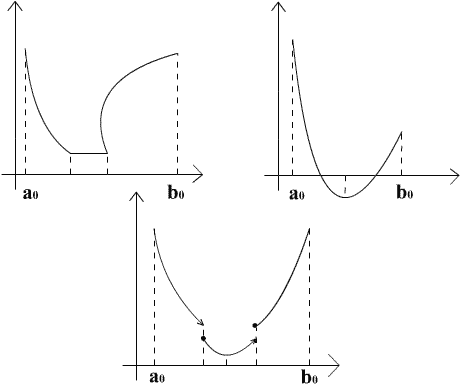
Это важное свойство унимодальных функций. Если мы знаем значения f в точках 
и 
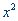отрезка [a,b], 
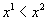, то мы можем определенно сказать на каком из отрезков 
лежит минимум x* функции f.
Действительно, возможны три различных результата:
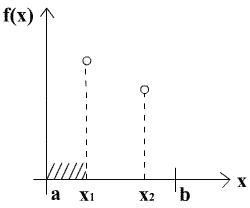
a)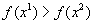 
. В этом случае интервал 
может быть отброшен.
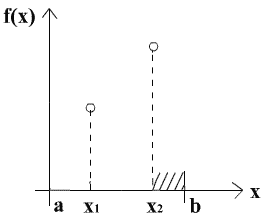
б) 
. В этом случае интервал 
может быть отброшен.
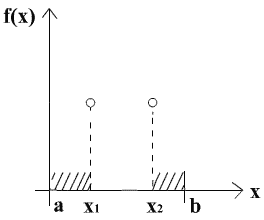
в) 
. В этом случае интервалы и могут быть отброшены.
Методы поиска на основе исключения интервалов указывают на отрезок, на котором гарантированно лежит точка x*. Этот отрезок называют отрезком неопределенности. Если в качестве приближенного значения x* взять центр этого отрезка, то погрешность метода есть половина длины отрезка неопределенности.
В отличии от методов исключения интервалов и полимиальной аппроксимации Методы с использованием производных позволяют построить гораздо более быстрые методы, основанные на решении уравнения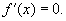 
Если целевая функция содержит члены, включающие x в третьей и более высоких степенях, то получение аналитического решения уравнения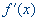 
затруднительно. В этих случаях целесообразно использовать численные методы нахождения корней нелинейных уравнений.
Итак, рассмотрим задачу нахождения единственного корня 
на отрезке [a,b] нелинейного уравнения f(x) = 0 в предположении непрерывности функции f(x).
Геометрически корень x* соответствует точке пересечения графика функции y= f(x) с осью Ох.
Определение 4.. Число x* - есть корень уравнения кратности k, если при x= x * вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно, т.е.:
Корень кратности k=1 называется простым.
Так на рисунке корни 
и 
– простые,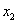 
- как минимум кратности 2, 
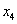как минимум кратности 3.
Если уравнения f(x) = 0 имеет на [a,b] несколько корней, то выполняется операция отделения (локализации) корней, т.е. нахождения достаточно малых окрестностей рассматриваемой области, в которых содержится одно значение корня данного уравнения. Для выявления отрезка, содержащего корень уравнения, следует построить график этой функции.
Для нахождения корней уравнения f(x) = 0 используются различные итерационные методы.
Суть итерационного метода состоит в следующем: генерируется последовательность приближений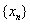 
,которая сходится к корню в том смысле, что 