Стратегия поиска.
Одним из самых эффективных и точных методов уточнения корней нелинейного уравнения является метод Ньютона.
Идея метода Ньютона заключается в том, что в окрестности имеющегося приближения 
задача f(x) =0 заменяется некоторой вспомогательной линейной задачей. Эта задача выбирается так, чтобы погрешность замены имела более высокий порядок малости, чем первый (порядок малости) в окрестности имеющегося приближения. За следующее приближение принимается решение этой вспомогательной задачи. Рассмотрим разложение функции f(x) в ряд Тейлора до членов 1-го порядка включительно в окрестности точки :
Тогда в качестве вспомогательной задачи берется линейная задача:
Ее решение 
принимается за следующее приближение 
к решению исходного уравнения, т.е. итерации ведутся по формуле:
.
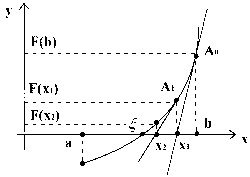
Таким образом, метод состоит в замене кривой y= f(x) на касательную к ней в процессе каждой итерации. Это видно из уравнения касательной, проведенной в точке 
из которого расчетная формула метода Ньютона получается, если положить y=0.
Достаточные условия сходимости определяются теоремой.
Теорема: Пусть f(х) определена и дважды дифференцируема на отрезке [а,b], причем
f(а), f(b)< 0, а производные 
и 
сохраняют знак на отрезке [а,b]. Тогда, исходя из начального приближения 
, удовлетворяющего неравенству 
, можно построить последовательность
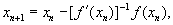, n=0,1,...
сходящуюся к единственному на отрезке [а,b] решению 
уравнения 
.
Для достижения заданной погрешности 
при использовании метода Ньютона потребуется порядка 
итераций.
Отметим, что метод Ньютона эффективен, если выбрано хорошее начальное приближение корня и график функции имеет большую крутизну в окрестности корня. В этом случае процесс быстро сходится, со скоростью геометрической прогрессии. Если же численное значение вблизи корня мало, т.е. график почти параллелен оси 0х, то выбор метода Ньютона вряд ли разумен. Отметим также, что если бы f(х) была линейной, то метод Ньютона нашел бы корень за одну итерацию
|
|
Алгоритм.
Шаг 1. На отрезке [a,b] задать начальное приближение 
и точность вычисления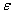 
Шаг 2. Вычислить очередное приближение по формуле:
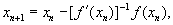где n=1,2,...
Шаг 3. Повторить процедуру 2 до тех пор, пока 
, тогда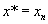 
.
Пример.
Задание.
Найти минимум функции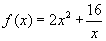 
положив 
, 
.
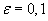Решение.
Методы многомерной оптимизации
Основные определения.
Рассмотрим следующую задачу
Определение 1.
Поверхностью уровня функции f(x) называется геометрическое место точек, такое что 
. В случае 2-х переменных поверхность уровня называется линией уровня.
Выделяют три основных типа рельефа поверхности: котловинный, овражный и неупорядоченный.
а) котловинный тип рельефа – линии уровня похожи на концентрические эллипсы. В малой окрестности невырожденного минимума рельеф функции котловинный.
б) овражный тип рельефа – линии уровня кусочно-гладкие. Если угол изло-ма направлен в сторону возрастания функции, то геометрическое место точек излома по всем линиям уровня называется истинным оврагом. Если угол излома направлен в сторону убывания функции, то геометрическое место точек излома по всем линиям уровня называется истинным гребнем.
На практике чаще линии уровня всюду гладкие, но на них имеются участки с большой кривизной.
|
|
Геометрическое место точек с набольшей крутизной называется разрешимым оврагом или гребнем.
в) неупорядоченный тип рельефа характеризуется наличием многих максимумов, минимумов и седловин. Примером может служить функция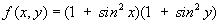 
имеющая минимумы в точках с координатами 
и максимумы в точках 
Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает, и отличаются друг от друга способом построения таких траекторий. При этом следует отметить, что метод, приспособленный к одному типу рельефа, может оказаться плохим при другом типе рельефа.
Определение 2.
Градиентом функции многих переменных f(x) называется вектор, составленный из первых частных производных функции по всем переменным:
т.е. градиент – это вектор-столбец размерности (n * 1), где n число перемен-ных функции.
Свойства градиента:
1. Градиент функции перпендикулярен касательной к линии уровня функ-ции f(x)
2. Направление градиента есть направление наиболее быстрого роста функции.
Вектор, противоположный градиенту 
, называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю.
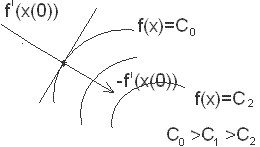
Определение 3.
Матрицей Гессе называется квадратная матрица размерности (n*n), составленная из вторых частных производных функции f(x) по всем переменным
