Стратегия поиска. Идея метода состоит в сравнении значений функции в (n+1)вершинах многогранника (симплекса) 
, i=1,…, n+1, k- номер итерации и перемещении в направлении оптимальной точки с помощью следующей итерационной процедуры. Точки многогранника 
на k+1 итерации совпадают с точками , за исключением худшей точки 
многогранника, т.е. той точки, в которой исходная функция принимает наибольшее значение. Точка заменяется на другую с помощью трех основных операций: отражения, растяжения, сжатия и редукции. В процессе выполнения данных операций многогранник изменяет свои размеры, что и обусловило название метода. Построение последовательности многогранников заканчивается, когда значения функции в вершинах многогранника отличается от значения функции в центре тяжести многогранника не более, чем на заданную величину.
Важный вопрос – построение начального симплекса. Задается некото-рая базовая точка 
, а координаты остальных n вершин симплекса получаются следующим образом:
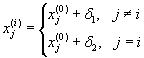где
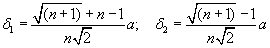, а a – масштабный множитель.
Например, если 
и остальные две вершины симплекса равны: 
Начальный симплекс можно построить иначе: 
, где 
- единичный вектор.
Например, если 
Алгоритм метода.
Начальный этап
Задать начальную точку и коэффициенты отражения 
, растяжения 
и сжатия 
. Сформировать начальный симплекс. Перейти к основному этапу.
Начальный этап
Шаг 1. Вычислить значение функции во всех точках многогранника и выбрать лучшую и худшую точки 
и 
. Вычислить центр тяжести многогранника за исключением худшей точки: 
Здесь h – номер худшей точки.(для функции 2-х переменных точка 
- середина отрезка, соединяющего точки за исключением худшей).
Шаг 2. Проверить условие окончания счета:
а) если
то поиск закончить 
;
б) иначе перейти к шагу 3.
Шаг 3. Выполнить операцию отражения худшей точки через центр тяжести:
Здесь 
– параметр отражения (рекомендуемое значение 
).
Шаг 4. Построение нового многогранника. Для этого вычисляется значение функции в точке 
, которое сравнивается со значением функции в Лучшей точке 
:
а) если, 
то выполняется операция растяжения:
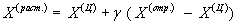
Здесь 
– параметр растяжения (рекомендуемое значение 
).
Если 
, то меняем точку 
на 
, если же 
, то меняем точку на
б) если 
, то выполняется операция сжатия: 
Здесь 
– параметр сжатия (рекомендуемое значение 
)
Если 
, то меняем худшую точку на 
, если же 
, то меняем точку на .
в) если 
, то выполняется операция редукции. В этом случае формируется новый многогранник, содержащий лучшую точку 
с уменьшенными вдвое сторонами: 
Перейти к шагу 1.
Пример.
Найти минимум функции 
Решение.
Т.к. n=2, то в качестве начального многогранника возьмем треугольник с вершинами 
. Положим 
Таким образом,
Проверим окончание счета. Так как 
то процесс продолжается.
Выполним операцию отражения худшей точки через центр тяжести.
Имеем: 
.
Так как 
выполним растяжение:
Так как 
,
то худшая вершина 
заменяется на вершину 
.
Итак новый многогранник содержит вершины: 
.
Переходим к шагу 1.
. Таким образом, 
Так как 
, то процесс продолжается. и т.д.
Методы первого порядка