Задачи поиска оптимума возникают при построении математических моделей. Когда для изучения какого-либо явления конструируется математическая модель, к оптимизации прибегают для того, чтобы определить ее структуру и параметры, которые обеспечивают наилучшее согласие с реальностью.
Пусть результат измерения случайной величины у зависит от 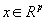 , причем
, причем 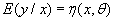 где у - результат измерения,
где у - результат измерения, 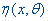 - функция, вид которой известен,
- функция, вид которой известен, 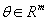 - неизвестные параметры функции. Оценка неизвестных параметров
- неизвестные параметры функции. Оценка неизвестных параметров  при определенных условиях может быть произведена, например, по методу наименьших квадратов посредством минимизации суммы квадратов
при определенных условиях может быть произведена, например, по методу наименьших квадратов посредством минимизации суммы квадратов
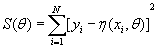
по 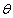 . Здесь N- количество наблюдений.
. Здесь N- количество наблюдений.
Для определения структуры модели, т.е. определение ее вида, создается множество альтернативных моделей, среди которых выбирается одна из моделей по некоторому критерию. В качестве критерия может выступать либо сумма квадратов  , либо оценка дисперсии модели, либо коэффициент детерминации и т.п.
, либо оценка дисперсии модели, либо коэффициент детерминации и т.п.
Задача Штейнера.
Классическая задача Штейнера формулируется так: требуется найти точку 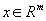 , сумма расстояний от которой до заданных точек
, сумма расстояний от которой до заданных точек 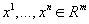 минимальна. Эта задача типично оптимизационная:
минимальна. Эта задача типично оптимизационная:
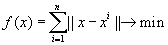
Приведенные задачи представляют собой задачи безусловной оптимизации — на искомое решение не налагается никаких дополнительных условий, кроме того, что оно должно доставлять минимум некоторой функции (другими словами, минимум функции ищется на всем пространстве — области определения функции).
3. Задача о рационе.
Формулировка задачи о рационе: Пусть имеется n различных пищевых продуктов, содержащих m различных питательных веществ. Обозначим через 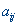 долю j-го питательного вещества в i-ом продукте, через
долю j-го питательного вещества в i-ом продукте, через  — суточную потребность организма в j-ом питательном веществе, через
— суточную потребность организма в j-ом питательном веществе, через  — стоимость единицы i-го продукта. Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных веществах. Если обозначить через
— стоимость единицы i-го продукта. Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных веществах. Если обозначить через 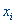 суточное потребление i-го продукта, то эта задача может быть формализована следующим образом. Нужно минимизировать функцию
суточное потребление i-го продукта, то эта задача может быть формализована следующим образом. Нужно минимизировать функцию 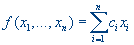 (стоимость рациона)
(стоимость рациона)
при условиях
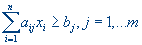 (рацион должен содержать не менее суточной потребности в каждом из питательных веществ).
(рацион должен содержать не менее суточной потребности в каждом из питательных веществ).
Очевидно, также следует требовать, чтобы 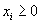 В векторных обозначениях задача о рационе может быть записана так: минимизировать функцию
В векторных обозначениях задача о рационе может быть записана так: минимизировать функцию
f(x)=(c,x), где 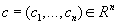 .
.
Эту задачу, как обычно, мы записываем в виде при ограничениях 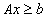 ,
, 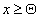 .В них первое неравенство связывает два вектора Ax и b из
.В них первое неравенство связывает два вектора Ax и b из 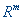 , а второе – два вектора x и
, а второе – два вектора x и  из
из 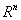 .
.
4. Транспортная задача.
Транспортная задача — классическая задача линейного программирования. К ней сводятся многие оптимизационные задачи. Формулируется она так. На m складах находится груз, который нужно развезти n потребителям. Пусть 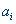 (i = 1,..., n) — количество груза на i-ом складе, а
(i = 1,..., n) — количество груза на i-ом складе, а  (j = 1,..., m) — потребность в грузе j-го потребителя,
(j = 1,..., m) — потребность в грузе j-го потребителя, 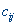 — стоимость перевозки единицы груза с i-го склада j-му потребителю. Требуется минимизировать стоимость перевозок. Если обозначить через
— стоимость перевозки единицы груза с i-го склада j-му потребителю. Требуется минимизировать стоимость перевозок. Если обозначить через  объем перевозок с i-го склада j-му потребителю, то транспортная задача формализуется так:
объем перевозок с i-го склада j-му потребителю, то транспортная задача формализуется так:
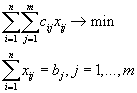 (все потребители должны быть удовлетворены),
(все потребители должны быть удовлетворены),
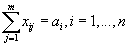 (весь груз должен быть доставлен потребителю),
(весь груз должен быть доставлен потребителю),
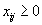 (нельзя перевозить груз от потребителя на склад).
(нельзя перевозить груз от потребителя на склад).
Это были примеры линейных задач условной оптимизации. Приведем один пример нелинейной задачи.
5. Задачи о распределении ресурсов.
Общий смысл задачи о распределении ресурсов — распределить ограниченный ресурс между потребителями оптимальным образом. Рассмотрим задачу о режиме работы энергосистемы. Пусть m электростанций питают одну нагрузку мощности p. Обозначим через  активную мощность, генерируемую j-ой электростанцией. Техническими условиями определяются возможный минимум
активную мощность, генерируемую j-ой электростанцией. Техническими условиями определяются возможный минимум 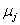 и максимум
и максимум 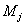 вырабатываемой j-ой электростанцией мощности. Допустим затраты на генерацию мощности x на j-ой электростанции равны
вырабатываемой j-ой электростанцией мощности. Допустим затраты на генерацию мощности x на j-ой электростанции равны 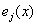 . Требуется сгенерировать требуемую мощность p при минимальных затратах.
. Требуется сгенерировать требуемую мощность p при минимальных затратах.
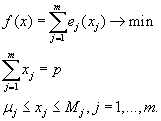
Безусловная оптимизация
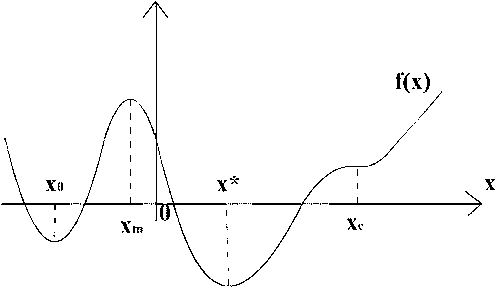
Задача безусловной оптимизации состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений. Несмотря на то что большинство практических задач оптимизации содержит ограничения, изучение методов безусловной оптимизации важно с нескольких точек зрения. Многие алгоритмы решения задачи с ограничениями предполагают сведение ее к последовательности задач безусловной оптимизации. Другой класс методов основан на поиске подходящего направления и последующей минимизации вдоль этого направления. Обоснование методов безусловной оптимизации может быть естественным образом распространено на обоснование процедур решения задач с ограничениями.
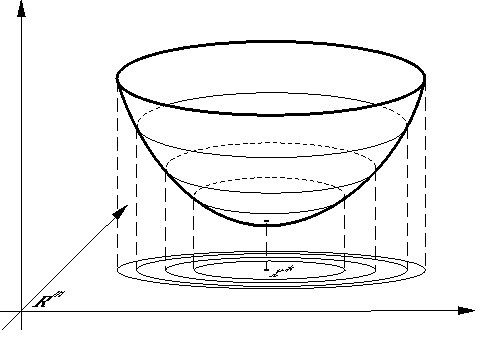
Условная оптимизация

Задача условной оптимизации заключается в поиске минимального или максимального значения скалярной функции f(x) n-мерного векторного аргументах. Решение задачи основывается на линейной или квадратичной аппроксимации целевой функции для определения приращений x1, …,xn на каждой итерации. Существуют также приближенные методы решения нелинейных задач. Это методы основанные на методе кусочно-линейной аппроксимации. Точность нахождения решений зависит от количества интервалов, на которых мы находим решение линейной задачи, максимально приближенной к нелинейной. Такой метод позволяет производить расчеты с помощью симплекс-метода. Обычно в линейных моделях коэффициенты целевой функции постоянны и не зависят от значения переменных. Однако существует ряд задач, где затраты зависят от объема нелинейно.
