Классификация задач оптимизации.

Кафедра Информатики и компьютерных технологий

Составитель: доц.: Г.Н. Журов

Математические методы в инженерии

Методы оптимизации систем автоматизированного проектирования

Конспект лекций для магистров

направления 151000 «Технологические машины и оборудование»

Санкт-Петербург

Содержание

Классификация задач оптимизации. 5

Оценка параметров и структуры математической модели. 6

Безусловная оптимизация. 8

Методы одномерной оптимизации. 10

Методы поиска экстремума функции одной переменной. 10

Основные понятия. 10

Классификация методов одномерной безусловной оптимизации. 11

Метод половинного деления (дихотомии) 15

Метод Золотого сечения. 18

Метод Фибоначчи. 21

Метод Пауэлла. 25

Метод секущих. 30

Метод Ньютона (метод касательных). 32

Методы многомерной оптимизации. 34

Основные определения. 34

Принципы построения численных методов. 38

Классы функций. 41

Классификация методов. 42

Методы нулевого порядка. 44

Метод конфигураций Хука-Дживса. 44

Метод деформируемого многогранника (метод Нелдера—Мида) 46

Методы первого порядка. 51

Метод градиентного спуска с постоянным шагом. 51

Метод наискорейшего спуска. 53

Метод Гаусса-Зейделя (наискорейшего покоординатного спуска). 56

Метод Флетчера-Ривса (Метод сопряженных градиентов). 60

Методы второго порядка. 64

Метод Ньютона. 64

Модификации метода Ньютона. Метод Ньютона-Рафсона. 68

Классификация задач оптимизации.

Методы оптимизации находят эффективное применение во всех направлениях инженерной и научной деятельности. При всем многообразии содержания конкретных оптимизационных задач они имеют общую форму. Все эти задачи можно классифицировать как задачи минимизации (максимизации) вещественнозначной функции f(х) n-мерного векторного аргумента компоненты которого удовлетворяют системе уравнений , набору неравенств , а также ограничены сверху и снизу, т. е. 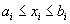. Функцию f(х) принято называть целевой функцией, уравнения — ограничениями в виде равенств, а неравенства — ограничениями в виде неравенств. При этом предполагается, что все фигурирующие в задаче функции являются вещественнозначными, а число ограничений конечно.

Итак, в самом общем виде задача оптимизации может быть сформулирована следующим образом:

f(x)->min (max), (1)

при ограничениях

, k=1,..., K, (2)

, j=1,..., J, (3)

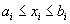, i=1,…, n (4).

В задаче (1)-(4), , 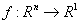- целевая функция, а множество точек , удовлетворяющих ограничениям (2)-(4) – это допустимое множество X.

Задача, в которой нет ограничений, т. е. J=K=0, и 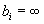, i=1,…, n называется оптимизационной задачей без ограничений или задачей безусловной оптимизации, в противном случае - задачей оптимизации с ограничениями или задачей условной оптимизации.

Задачи оптимизации классифицируются в соответствии с видом функций f, h, g и размерностью вектора X. Задачи без ограничений, в которых X представляет собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но вместе с тем весьма важный подкласс оптимизационных задач. Задачи условной оптимизации, в которых функции h, g являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи, которые содержат только линейные функции вектора непрерывных переменных X, называются задачами линейного программирования; в задачах целочисленного программирования компоненты вектора X должны принимать только целые значения. Задачи с нелинейной целевой функцией и линейными ограничениями иногда называют задачами нелинейного программирования с линейными ограничениями. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций. Если f(x) — квадратичная функция, то мы имеем дело с задачей квадратичного программирования; если f(x) есть отношение линейных функций, то соответствующая задача носит название задачи дробно-линейного программирования. Если функции f(x), , зависят также от случайных параметров w, где w является элементом пространства случайных параметров , тогда имеем задачу стохастического программирования. Деление оптимизационных задач на эти классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения.

Рассмотрим ряд примеров оптимизационных задач.