Стратегия поиска. Метод представляет собой комбинацию исследующего поиска с циклическим изменением переменных и ускоряющего поиска по образцу. Цель исследующего поиска – выявление локального поведения целевой функции и определение направления ее убывания. Эта информация используется при поиске по образцу вдоль направления убывания целевой функции.
Исследующий поиск начинается из некоторой начальной точки  , называемой старым базисом. В качестве множества направлений поиска выбирается множество координатных направлений. Задается величина шага, которая может быть различной для разных координатных направлений. Фиксируется первое координатное направление и делается шаг в сторону увеличения соответствующей переменной. Если значение исходной функции f(x) в пробной точке меньше значения функции в исходной точке, то шаг считается удачным. В противном случае из исходной точки делается шаг в противоположном направлении с последующей проверкой поведения функции. Если и в этом случае не происходит уменьшения функции, то происходит уменьшение шага и процедура повторяется. Исследующий поиск по данному направлению заканчивается, когда текущая величина шага становится меньше некоторой величины. После перебора всех координат исследующий поиск завершается, полученная точка называется новым базисом.
, называемой старым базисом. В качестве множества направлений поиска выбирается множество координатных направлений. Задается величина шага, которая может быть различной для разных координатных направлений. Фиксируется первое координатное направление и делается шаг в сторону увеличения соответствующей переменной. Если значение исходной функции f(x) в пробной точке меньше значения функции в исходной точке, то шаг считается удачным. В противном случае из исходной точки делается шаг в противоположном направлении с последующей проверкой поведения функции. Если и в этом случае не происходит уменьшения функции, то происходит уменьшение шага и процедура повторяется. Исследующий поиск по данному направлению заканчивается, когда текущая величина шага становится меньше некоторой величины. После перебора всех координат исследующий поиск завершается, полученная точка называется новым базисом.
Поиск по образцу заключается в движении по направлению от старого базиса к новому. Величина ускоряющего шага задается ускоряющим множи-телем  . Успех поиска по образцу определяется с помощью исследующего поиска из полученной точки. Если значение функции в наилучшей точке меньше, чем в точке предыдущего базиса, то поиск по образцу удачен, в противном случае происходит возврат в новый базис, где продолжается исследующий поиск с уменьшенным шагом.
. Успех поиска по образцу определяется с помощью исследующего поиска из полученной точки. Если значение функции в наилучшей точке меньше, чем в точке предыдущего базиса, то поиск по образцу удачен, в противном случае происходит возврат в новый базис, где продолжается исследующий поиск с уменьшенным шагом.
Обозначим через 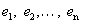 – координатные направления:
– координатные направления:

Отметим, что при поиске по направлению  меняется только переменная
меняется только переменная  , а остальные переменные остаются зафиксированными.
, а остальные переменные остаются зафиксированными.
Алгоритм метода.
Шаг 1. Задать начальную точку  , число
, число  - для остановки алгоритма, начальные значения приращений по координатным приращениям
- для остановки алгоритма, начальные значения приращений по координатным приращениям  , ускоряющий множитель
, ускоряющий множитель 
Шаг 2. Провести исследующий поиск по выбранному координатному направлению:

Шаг 3. Проверить условия:
а) если i < n, то положить i= i+1 и перейти к шагу 2. (продолжить исследующий поиск по оставшимся направлениям);
б) если i = n, проверить успешность исследующего поиска:
- если  , перейти к шагу 4.
, перейти к шагу 4.
- если  , перейти к шагу 5.
, перейти к шагу 5.
Шаг 4. Провести поиск по образцу.
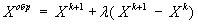
В точке  провести исследующий поиск, в результате которого получается точка
провести исследующий поиск, в результате которого получается точка 
Если  , то точка
, то точка  становится точкой нового базиса, а
становится точкой нового базиса, а  - точкой старого базиса. Перейти к шагу 5..
- точкой старого базиса. Перейти к шагу 5..
Если  , то поиск по образцу считается неудачным, точки
, то поиск по образцу считается неудачным, точки  ,
,  аннулируются, точка
аннулируются, точка  остается точкой нового базиса, а
остается точкой нового базиса, а  - точкой старого базиса. Перейти к шагу 2.
- точкой старого базиса. Перейти к шагу 2.
Шаг 5. Проверить условие окончания счета:
а) если все  , то поиск закончить
, то поиск закончить 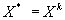 ;
;
б) для тех i, для которых  , уменьшить величину шага и перейти к шагу 2.
, уменьшить величину шага и перейти к шагу 2.
Пример.
Найти минимум функции 
Решение.
 Зададим начальную точку
Зададим начальную точку  ; число
; число  . Положим i=1, k=0.
. Положим i=1, k=0.
 , то шаг неудачен.
, то шаг неудачен.  , то шаг удачен.
, то шаг удачен.
 Поскольку i=1 <2=n, то положим i=2 и перейдем к шагу 2.
Поскольку i=1 <2=n, то положим i=2 и перейдем к шагу 2.

 , то шаг неудачен.
, то шаг неудачен.
 ,то шаг удачен
,то шаг удачен
 Поскольку i=2=n и
Поскольку i=2=n и  , то перейдем к шагу 4.
, то перейдем к шагу 4.
 Проведем поиск по образцу из точки
Проведем поиск по образцу из точки  Положим i=1, k= k+1=1.
Положим i=1, k= k+1=1.  и перейдем к шагу 2.
и перейдем к шагу 2.
 Выполняем исследующий поиск из точки
Выполняем исследующий поиск из точки  .
. 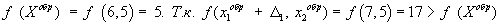 , то шаг неудачен. Т.к.
, то шаг неудачен. Т.к. 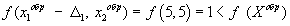 , то шаг удачен.
, то шаг удачен.
 Поскольку i=1 <2=n, то положим i= i+1=2 и перейдем к шагу 2.
Поскольку i=1 <2=n, то положим i= i+1=2 и перейдем к шагу 2.
 , то шаг неудачен.
, то шаг неудачен.  , то шаг неудачен.
, то шаг неудачен.

 , то поиск по образцу на шаге 40 прошел успешно.
, то поиск по образцу на шаге 40 прошел успешно.
Точка  становится новым базисом, а точка
становится новым базисом, а точка  становится старым базисом. Выполним поиск по образцу из нового базиса. Перейдем к шагу 4.
становится старым базисом. Выполним поиск по образцу из нового базиса. Перейдем к шагу 4.
 Положим i=1, k= k+1=2.
Положим i=1, k= k+1=2.  и перейдем к шагу 2.
и перейдем к шагу 2.
 , то шаг удачен.
, то шаг удачен.
 Поскольку i=1 <2=n, то положим i= i +1=2 и перейдем к шагу 2.
Поскольку i=1 <2=n, то положим i= i +1=2 и перейдем к шагу 2.
 , то шаг удачен.
, то шаг удачен.
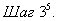 Т.к. i=2=n и f(4,5)=5 > f(5,5)=1, то поиск по образцу на
Т.к. i=2=n и f(4,5)=5 > f(5,5)=1, то поиск по образцу на  прошел неудачно. Переходим к шагу 5.
прошел неудачно. Переходим к шагу 5.
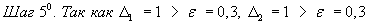 , то следует уменьшить шаг. Положим
, то следует уменьшить шаг. Положим  , за базис возьмем точку (5,5) и повторим цикл вычислений с новым базисом и новыми значениями шагов. Минимум достигается в точке
, за базис возьмем точку (5,5) и повторим цикл вычислений с новым базисом и новыми значениями шагов. Минимум достигается в точке 