Применение необходимых и достаточных условий безусловного экс-тремума функции многих переменных эффективно при решении ограничен-ного числа задач, в которых вытекающие из условий соотношения имеют аналитическое решение. В большинстве практических ситуациях они не мо-гут быть использованы по следующим причинам:
1. Целевая функция f(x) может не иметь непрерывных производных до второго порядка включительно.
2. Использование необходимых условий сводит решение задачи оптими-зации к решению системы п нелинейных алгебраических уравнений, что представляет собой самостоятельную задачу, трудоемкость реше-ния которой сравнима с трудоемкостью численного решения исходной задачи.
3. Функция, вообще, может быть не задана аналитически.
Наиболее распространенные и эффективные методы приближенного решения задачи безусловной оптимизации 
укладываются в следующую грубую схему. Начиная с некоторого 
, строится последовательность 
такая, что 
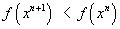
Такие последовательности называются релаксационными, а методы по-строения релаксационных последовательностей — итерационными метода-ми или методами спуска.
Определение 1.
Последовательность 
называется минимизирующей, если 
т.е. последовательность сходится к нижней грани f(x).
Определение 2.
Последовательность называется сходящейся к точке минимума, если
.
Отметим, что не всякая минимизирующая последовательность является сходящейся.
Пример 1.
Классифицировать последовательность 
для функции 
Решение.
Минимум этой функции достигается в точке 
.Последовательность 
для функции является минимизирующей, т.к. 
, однако она не сходится к точке минимума 
, т.к.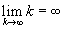 
Пример 2.
Классифицировать последовательность , заданную правилом 
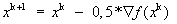для функции 
Решение.
Минимум этой функции достигается в точке 
, 
Таким образом, последовательность является и минимизирующей, и сходящейся.
Работоспособность метода еще не гарантирована доказательством схо-димости соответствующей последовательности. Нужна определенная ско-рость сходимости.
Рассмотрим последовательность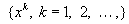 
сходящуюся к точке минимума 
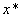. Будем предполагать, что все элементы последовательности различны и не совпадают с .
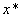Определение 3.
Последовательность называется сходящейся с порядком r, если r – максимальное число, для которого 
При r =1 говорят о линейной скорости сходимости или о сходимости со скоростью геометрической прогрессии, что может быть представлено в виде неравенства для достаточно больших k
,
где 
а при 
говорят о сверхлинейной скорости сходимости.
При r=2 говорят о квадратичной скорости сходимости 
Пример 1.
Определить порядок сходимости последовательности 
, где 
Решение.
Каждый следующий член этой последовательности равен квадрату предыдущего, а ее предел равен нулю. В соответствии с определением имеем
поэтому сходимость квадратическая.
Пример 2.
Определить порядок сходимости последовательности 
, где
Решение.
Каждый следующий член этой последовательности равен квадратным корнем предыдущего, а ее предел при любом a > 0 равен единице.
В соответствии с определением имеем
, поэтому сходимость линейная.
Пример 3.
Определить порядок сходимости последовательности 
, где k=0,1,2,….
Решение.
Последовательность 
сходится к 
, поэтому сходимость линейная.
Пример 4.
Определить порядок сходимости последовательности 
, где k=1,2,….
Решение.
Последовательность 
сходится к
Т.к. r=1 и c=0, то сходимость сверхлинейная.
Классы функций.
Особенно легко вопросы существования и единственности решаются для выпуклых функций. Эти функции являются очень важным объектом в теории оптимизационных задач. Введем ряд определений.
Определение 1.
Функция f(x), 
называется выпуклой, если при всех
Если неравенство строгое, то f называется строго выпуклой.
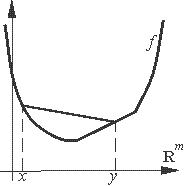
Геометрически выпуклость означает, что график функции на интервале (x, y), соединяющем любые точки x и y, лежит не выше прямой, соединяющей точки (x, f(x)) и (y, f(y)).
Определение 2.
Функция f(x),определенная на 
называется 
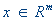называется сильно выпуклой с константой l > 0, если при всех
Геометрически это понятие можно интерпретировать так.
Пусть точки отрезка [x, y], соединяющего точки x и y, параметризованы параметром 
. Правая часть неравенства определяет на этом отрезке полином 
второго порядка (от 
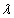).График сильно выпуклой функции над отрезком [x, y] должен лежать ниже параболы — графика этого полинома.
Для дифференцируемой функции f(x), 
выпуклость эквивалентна неравенству
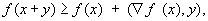
или
строгая выпуклость – неравенству
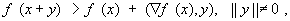
или
сильная выпуклость – неравенству
или
или
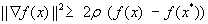
Для дифференцируемой сильно выпуклой функции f(x) точка минимума 
существует, единственна и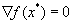 
Классификация методов.
Детерминированные алгоритмы безусловной минимизации делят на классы в зависимости от вида используемой информации для формирования направления перехода. Если на каждой итерации используются лишь значения минимизируемых функций, то метод называется методом нулевого порядка. Если, кроме того, требуется вычисление первых производных минимизируемой функции, то имеют место методы первого порядка, при необходимости дополнительного вычисления вторых производных - методы второго порядка.