Стратегия поиска. Рассмотренные выше градиентные методы отыскивают точку минимума функции в общем случае лишь за бесконечное число итераций. Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции.
Определение. Два n-мерных вектора х и у называют сопряженными по отношению к матрице H (или H-сопряженными), если скалярное произведение (x, Ну) = 0. Здесь Н - симметрическая положительно определенная матрица размером пхп.
Стратегия метода Флетчера-Ривса состоит в построении последовательности точек 
, k=0, 1, 2,... таких, что 
, k=0, 1, 2,...
Точки последовательности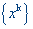 
вычисляются по правилу:
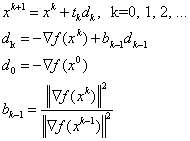
Величина шага выбирается из условия минимума функции f(х) по t в направлении движения, т. е. в результате решения задачи одномерной минимизации:
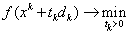
Отметим, что при данном выборе 
в случае квадратичной функции f(x)= (х, Нх) + (b, х) + а направления 
будут H-сопряженными, т.е. 
При этом в точках последовательности градиенты функции f(x) взаимно перпендикулярны, т.е.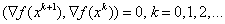 
При минимизации неквадратичных функций метод Флетчера-Ривса не является конечным. Для неквадратичных функций используется следующая модификация метод Флетчера-Ривса (метод Полака-Рибьера), когда величина 
вычисляется следующим образом:
Здесь I- множество индексов: I = {0, n, 2n, Зn,...}, т. е. метод Полака-Рибьера предусматривает использование итерации наискорейшего градиентного спуска через каждые n шагов с заменой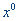 
на 
.
Построение последовательности заканчивается в точке, для которой 
.
Геометрический смысл метода сопряженных градиентов состоит в следующем. Из заданной начальной точки 
осуществляется спуск в направлении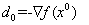 
. В точке 
определяется вектор-градиент 
. Поскольку 
является точкой минимума функции в направлении 
, то ортогонален вектору . Затем отыскивается вектор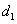 
, H-сопряженный к . Далее отыскивается минимум функции вдоль направления 
и т. д.
Алгоритм метода
Начальный этап Сходимость метода.
Теорема 3. Если квадратичная функция f(x) = (х, Нх) + (b, х) + а с неотрицательно определенной матрицей Н достигает своего минимального значения на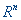 
, то метод Флетчера-Ривса обеспечивает отыскание точки минимума не более чем за n шагов.
Теорема 4.Пусть функция f(x) дифференцируема и ограничена снизу на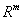 
, а ее градиент удовлетворяет условию Липшица
Тогда при произвольной начальной точке 
для метода Полака-Рибьера имеем
Отметим, что теорема 4 гарантирует сходимость последовательности к стационарной точке 
, где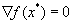 
. Поэтому найденная точка нуждается в дополнительном исследовании для ее классификации. Метод Полака-Рибьера гарантирует сходимость последовательности к точке минимума только для сильно выпуклых функций.
Оценка скорости сходимости получена только для сильно выпуклых функций, в этом случае последовательность сходится к точке минимума функции f(x)со скоростью:
Пример.
Решение.
Итерация 0.
Итерация 1.
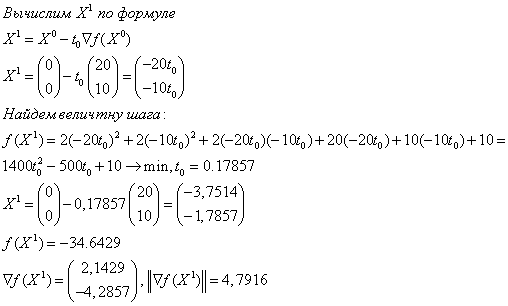
Задать , 
.
Найти градиент функции в произвольной точке
Положить k=0.
Основной этап
Шаг 1. Вычислить 
Шаг 2. Проверить выполнение критерия останова 
а) если критерий выполнен, расчет окончен, 
б) если критерий не выполнен, то перейти к шагу 3, если k=0, иначе к шагу 4.
Шаг 3. Определить
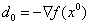
Шаг 4. Определить
или в случае неквадратичной функции
Шаг 5. Определить
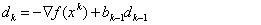
Шаг 6. Вычислить величину шага 
из условия
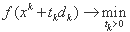
Шаг 7. Вычислить
Шаг 8. Положить k= k +1 и перейти к шагу 1.
Итерация 2.
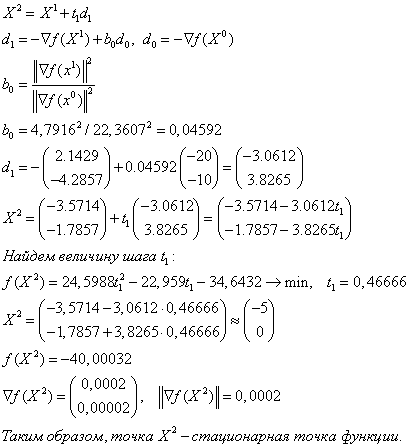
Анализ точки. Найдем матрицу Гессе функции
Так как матрица Гессе является положительно определенной, то функция f(X) строго выпукла и, следовательно, в стационарной точке достигает глобальный минимум.
Методы второго порядка
Метод Ньютона.
Стратегия поиска. Методы первого порядка используют линейную аппроксимацию целевой функции. Методы второго порядка, к которым относится метод Ньютона, возникли из квадратичной аппроксимации целевой функции.
Стратегия метода Ньютона состоит в построении последовательности точек 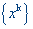, k=0, 1,... таких, что , k=0, 1,...
Точки последовательности 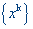вычисляются по правилу:
где 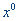– задается пользователем, а направление спуска 
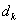вычисляется по формуле:
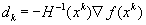
Такой выбор направления спуска гарантирует выполнение требования при условии, что матрица Гессе 
положительно определена. Чтобы обеспечить выполнение требования даже в тех случаях, когда для каких либо значений матрица Гессе не окажется положительно определенной, рекомендуется для соот-ветствующих значений k вычислить точку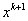 
по методу градиентного спуска 
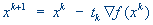с выбором величины шага из условия
К методу Ньютона можно придти из следующих соображений.
Необходимым условием экстремума функции многих переменных f(x) в точке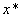 
является равенство нулю ее градиента в этой точке:
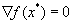
Функция f(х) в окрестности точки 
может быть разложена в ряд Тейлора с точностью до членов второго порядка:
Направление 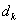определяется из необходимого условия экстремума первого порядка:
.
Имеем
При выполнении условия о положительной определенности матрицы получим:
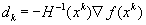
Таким образом, решение задачи методом Ньютона предполагает построение последовательности минимумов аппроксимирующих квадратичных функций 
.
В случае двух переменных данный метод имеет следующую геометрическую интерпретацию.
Построение последовательности заканчивается в точке, для которой
Если функция f(x) является квадратичной, то, независимо от начального приближения 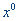и степени овражности, с помощью метода Ньютона ее минимум находится за один шаг. Действительно, в этом случае аппроксимирующая функция 
совпадает с f(x) и метод Ньютона при положительной определенности матрицы Гессе отыщет минимум за один шаг.
Алгоритм метода
Начальный этап
Задать , .
Найти градиент функции в произвольной точке
и матрицу Гессе H(x)
Положить k=0.
Основной этап
Шаг 1. Вычислить 
Шаг 2. Проверить выполнение критерия останова
а) если критерий выполнен, расчет окончен,
б) если критерий не выполнен, то перейти к шагу 3.
Шаг 3. Вычислить матрицу Гессе
Шаг 4. Найти обратную матрицу 
Шаг 5. Проверить положительную определенность матрицы
Шаг 6. Найти
Шаг 7. Положить k= k +1 и перейти к шагу 1.
Сходимость метода.
Теорема 5. Пусть функция f(x) дважды непрерывно дифференцируемая сильно выпуклая функция с константой l > 0 на 
, и удовлетворяет условию
а начальная точка такова, что
Тогда последовательность сходится к точке минимума с квадратичной скоростью 
Пример.
Решение.
Начальный этап
Положим 
Градиент функции есть:
Матрица Гессе
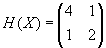
Положим k=0
Основной этап
Анализ точки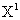 
. Функция является строго выпуклой функцией, так как ее матрица вторых производных
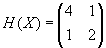
по критерию Сильвестра является положительно определенной. Действительно 
. Точка 
есть точка глобального минимума функции f(X).