В рекламной деятельности стоит задача: необходимо распространить N единиц рекламной продукции какого-либо одного средства рекламы по S районам, в которых проживают потенциальные потребители, различающиеся своим потребительским поведением. Из проведенных маркетинговых исследований известно, что если направить x 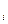 рекламной продукции в район I, то действенность (D) или эффективность рекламы составит D
рекламной продукции в район I, то действенность (D) или эффективность рекламы составит D 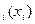 .Цель рекламодателя состоит в нахождении такого плана распределения N единиц рекламы по M=1,2,…,m районам, чтобы получить максимальную действенность рекламы.Действенность рекламы может выражаться в объемах продаж, увеличении числа посетителей рекламируемого магазина, увеличении числа повторных покупок или в проценте информированных о товаре через рекламу. В такой постановке задача ограничивается одним средством рекламы, например, распространением печатной рекламы по спальным районам, рекламы по кабельном каналу, щитовая реклама на улицах и т.д.
.Цель рекламодателя состоит в нахождении такого плана распределения N единиц рекламы по M=1,2,…,m районам, чтобы получить максимальную действенность рекламы.Действенность рекламы может выражаться в объемах продаж, увеличении числа посетителей рекламируемого магазина, увеличении числа повторных покупок или в проценте информированных о товаре через рекламу. В такой постановке задача ограничивается одним средством рекламы, например, распространением печатной рекламы по спальным районам, рекламы по кабельном каналу, щитовая реклама на улицах и т.д.
В такой постановке задача классического динамического программирования примет вид:
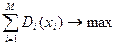 при ограничениях
при ограничениях 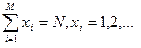
Примем d 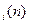 -действенность рекламы при оптимальном распределении n единиц из N по районам 1,2,…,i,x
-действенность рекламы при оптимальном распределении n единиц из N по районам 1,2,…,i,x 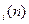 -количество рекламы, направленной на район i и создающей действенность d
-количество рекламы, направленной на район i и создающей действенность d 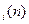 Тогда рекуррентное соотношение динамического программирования запишется в виде:
Тогда рекуррентное соотношение динамического программирования запишется в виде:
d 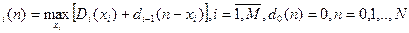
Максимум функции d 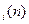 берется только по неотрицательным целочисленным значениям x
берется только по неотрицательным целочисленным значениям x 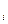 , удовлетворяющим условию x
, удовлетворяющим условию x 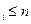 .
.
При известных значениях функции действенности рекламы D 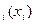 и N вычисления при решении задачи начинают с определения значений d
и N вычисления при решении задачи начинают с определения значений d 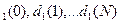 при i=1.Затем вычисляются значения d
при i=1.Затем вычисляются значения d 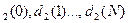 и так последовательно до значения d
и так последовательно до значения d 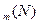 .Оптимальное распределение находится путем осуществляемое в обратном порядке выбора значений x
.Оптимальное распределение находится путем осуществляемое в обратном порядке выбора значений x 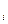 , дающих в совокупности d
, дающих в совокупности d 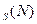 .
.
Рассмотрим модель общего вида в распределении рекламных усилий при нелинейном ограничении r 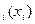 - i-ое средство рекламы (носитель рекламы, медиаканал и т.д.), состоящее из x
- i-ое средство рекламы (носитель рекламы, медиаканал и т.д.), состоящее из x 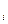 единиц рекламной продукции. Она по аналогии с вышерассмотренной запишется в виде:
единиц рекламной продукции. Она по аналогии с вышерассмотренной запишется в виде:
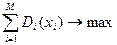 при
при 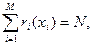 где x
где x 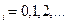 при любом i.
при любом i.
Из постановки задачи следует, что r 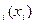 –неубывающая функция, удовлетворяющая условию r
–неубывающая функция, удовлетворяющая условию r 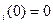 Для упрощения решения примем, что r
Для упрощения решения примем, что r 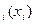 =x
=x 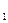 вследствие чего допустимое решение существует при любом значении N. Тогда рекуррентное соотношение динамического программирования примет вид:
вследствие чего допустимое решение существует при любом значении N. Тогда рекуррентное соотношение динамического программирования примет вид:
d 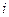 (n)=
(n)= 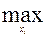
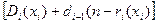 ,i=
,i= 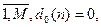 при i=0,n=0,1,…,N,r
при i=0,n=0,1,…,N,r 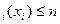
В оптимизационной задаче отыскивается значение d 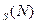 путем последовательного вычисления значений каждой функции d
путем последовательного вычисления значений каждой функции d 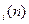 при n =0,1,…,N Начиная с i=1 до i=S.
при n =0,1,…,N Начиная с i=1 до i=S.
Рассмотрим задачу распределения усилий с двумя ограничениями. Рекламодатель планирует проведение рекламной кампании в одном из районов по определенному медиаканалу. В районе имеется S рекламоносителей. Для каждого i рекламоносителя известна действенность рекламы D 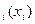 , как чистый доход с вычетом расходов на рекламу с выделенной суммой x
, как чистый доход с вычетом расходов на рекламу с выделенной суммой x 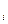 денег рекламного бюджета на оплату медиаканалу. Величина рекламного бюджета составляет N денежных единиц. Рекламодатель установил, что количество показов рекламного сообщения в течение дня не должно превышать числа M. Медиаканал i согласен осуществить показ K
денег рекламного бюджета на оплату медиаканалу. Величина рекламного бюджета составляет N денежных единиц. Рекламодатель установил, что количество показов рекламного сообщения в течение дня не должно превышать числа M. Медиаканал i согласен осуществить показ K 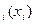 рекламы за сумму x
рекламы за сумму x 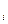 денег. Оптимизационная модель задачи запишется в виде
денег. Оптимизационная модель задачи запишется в виде
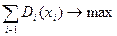 при ограничениях
при ограничениях
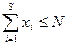 (общая сумма рекламного бюджета) x
(общая сумма рекламного бюджета) x 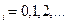 при любом i
при любом i
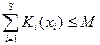 (число показов рекламы за день)
(число показов рекламы за день)
Соответствующее задаче рекуррентное соотношение будет иметь вид
d 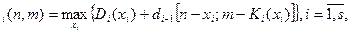
где n=0,1,…,N,m=0,1,…,M, x 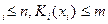
Функция d 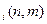 представляет собой доход от оптимального распределения рекламного бюджета по медиаканалам в зависимости от частоты показов рекламы в день. Задача решается аналогично ранее рассмотренной.
представляет собой доход от оптимального распределения рекламного бюджета по медиаканалам в зависимости от частоты показов рекламы в день. Задача решается аналогично ранее рассмотренной.
Аналогичная постановка задачи с двумя ограничениями состоит в следующем. Рекламодатель рассматривает распределение рекламного бюджета по s средствам рекламы или медиаканалам. Для осуществления варианта I 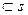 требуется выделить сумму в K
требуется выделить сумму в K 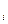 денежных единиц из рекламного бюджета. Величина рекламного бюджета составляет М, и она строго фиксирована Действенность рекламы от вложений по i-м варианту составляет D
денежных единиц из рекламного бюджета. Величина рекламного бюджета составляет М, и она строго фиксирована Действенность рекламы от вложений по i-м варианту составляет D 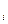 единиц. Рекламодатель стремится максимизировать действенность рекламы по s медиаканалам. Рекламодатель принимает решение, что количество медиаканалов не должно превышать величины N. Каждый вариант решения уникален и нужно решить, принимать его или отвергнуть в данной рекламной кампании.
единиц. Рекламодатель стремится максимизировать действенность рекламы по s медиаканалам. Рекламодатель принимает решение, что количество медиаканалов не должно превышать величины N. Каждый вариант решения уникален и нужно решить, принимать его или отвергнуть в данной рекламной кампании.
Примем, что переменная x 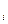 , сопоставляемая i–у варианту, может принимать только значения: x
, сопоставляемая i–у варианту, может принимать только значения: x 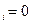 (вариант отвергнуть) или x
(вариант отвергнуть) или x 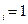 (вариант принять).Перечисленные условия запишутся в виде следующей модели.
(вариант принять).Перечисленные условия запишутся в виде следующей модели.
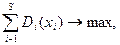
При ограничениях 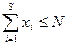 (число медиаканалов), x
(число медиаканалов), x 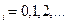 при любом i
при любом i
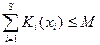 (объем рекламного бюджета), x
(объем рекламного бюджета), x 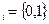 при любом i
при любом i
В этой задаче d 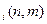 есть доход рекламодателя от оптимального распределения m единиц рекламного бюджета по n медиаканалам, выбранным из варианта1,2,…,
есть доход рекламодателя от оптимального распределения m единиц рекламного бюджета по n медиаканалам, выбранным из варианта1,2,…,
Рассмотрим другой класс задач в распределении рекламных усилий. Рекламодатель планирует поделить рекламный бюджет между s медиаканалами. Для каждого медиаканала в планировании рекламного бюджета имеется деление бюджета на три составляющие.Отчисления первой группы соответствуют исследованиям рекламы, т.е. на i–й медиаканал на его рекламные исследования выделяется v 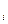 средств бюджета с ожидаемой действенностью рекламы от этого этапа P
средств бюджета с ожидаемой действенностью рекламы от этого этапа P 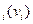 денежных единиц. Отчисления второй группы представляют затраты на апробацию рекламы на фокус-группе по i-му медиаканалу. На второй этап выделяется w
денежных единиц. Отчисления второй группы представляют затраты на апробацию рекламы на фокус-группе по i-му медиаканалу. На второй этап выделяется w 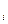 средств бюджета, что может принести в будущем доход рекламодателю в размере Q
средств бюджета, что может принести в будущем доход рекламодателю в размере Q 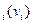 .К третьей группе относят затраты, связанные с показом рекламы по медиаканалу. Затраты третьей группы x
.К третьей группе относят затраты, связанные с показом рекламы по медиаканалу. Затраты третьей группы x 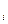 должны принести D
должны принести D 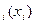 дохода от рекламы по i-му медиаканалу.
дохода от рекламы по i-му медиаканалу.
Общая сумма маркетинговых отчислений на рекламу (рекламный бюджет) составляет N.Однако, директор по маркетингу может установить верхний предел L 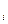 отчислений рекламного бюджета на i-й медиаканал. Задача менеджера по рекламе состоит в распределении рекламного бюджета таким образом, чтобы обеспечивать максимизацию общего дохода рекламодателя при наложенных ограничениях.
отчислений рекламного бюджета на i-й медиаканал. Задача менеджера по рекламе состоит в распределении рекламного бюджета таким образом, чтобы обеспечивать максимизацию общего дохода рекламодателя при наложенных ограничениях.
Математическая модель задачи описывается следующими соотношениями:
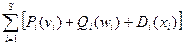
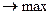 при ограничениях
при ограничениях
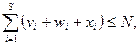
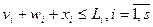
Рекуррентное отношение для данной задачи запишется в виде,
Где максимизация должна удовлетворить условию, тогда эту задачу также можно решить методом перебора.
Таким образом, используя динамические модели распределения рекламных усилий, можно повысить рентабельность рекламной деятельности, сократить время на обдумывания множества вариантов решений, улучшить технологию принятия решений, принять оптимальные решения.
Пример 15
Необходимо принять решение для финансирования двух видов рекламы: X 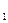 -реклама в газете1 и X
-реклама в газете1 и X 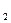 –реклама в газете 2. Рекламные газеты и рекламные блоки характеризуются двумя показателями – запоминаемости и эмоциональности. Известны следующие данные: один рекламный блок в газете 1 соответствует фактору запоминаемости в1 балл и 1 балл эмоциональности по 5-ти бальной шкале. Реклама в газете 2 соответствует 2 баллам запоминаемости и 4 баллам эмоциональности. По рыночным ценам один блок рекламы в газете 1 стоит 6 у.е., цена в газете 2 стоит 21 у.е. Эти данные можно записать в виде таблицы:
–реклама в газете 2. Рекламные газеты и рекламные блоки характеризуются двумя показателями – запоминаемости и эмоциональности. Известны следующие данные: один рекламный блок в газете 1 соответствует фактору запоминаемости в1 балл и 1 балл эмоциональности по 5-ти бальной шкале. Реклама в газете 2 соответствует 2 баллам запоминаемости и 4 баллам эмоциональности. По рыночным ценам один блок рекламы в газете 1 стоит 6 у.е., цена в газете 2 стоит 21 у.е. Эти данные можно записать в виде таблицы:
Таблица 1.18
| Наименование атрибута | Единица атрибута рекламы | Потребность | |
| Газета 1 | Газета2 | ||
| Стоимость блока рекламы, у.е. | p 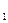 =6 =6
| p 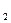 =21 =21
| |
| Запоминаемость, балл | a 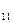 =1 =1
| a 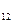 =2 =2
| b 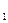 =3 =3
|
| Эмоциональность, балл | a 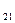 =1 =1
| a 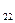 =4 =4
| b 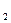 =4 =4
|
По данным приведенной таблицы экономико-математическая задача линейного программирования формулируется следующим образом. Найти значения покупок рекламы по величине рекламных блоков в газетах 1 и2 при условии минимума функции Z=6X 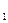 +21X
+21X 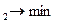 и при ограничениях:
и при ограничениях:
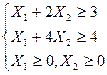
Ограничивающие соотношения суть неравенство, выражающее требование, чтобы реклама воздействовала в соответствии с принятой нормой. Таким образом, в задаче требуется минимизировать функцию Z. Например, можно определить минимум Z при условии выполнения одного ограничения X 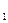 +2X
+2X 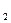 =3 Подставим в уравнение Z= 6X
=3 Подставим в уравнение Z= 6X 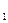 +21X
+21X 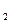 значение X
значение X 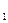 =3-2X
=3-2X 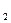 из этой же системы уравнений:
из этой же системы уравнений:
Z=6X 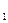 +21X
+21X 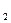 =18+9X
=18+9X 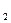
и минимум выражения Z получится при X 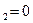 , а значит X
, а значит X 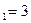 . Следовательно, минимальный рекламный бюджет рекламодателя составит 18 у.е., если покупать 3 блока рекламы в газете 1 или устроенную площадь или рекламное место в газете в 3 раза выгоднее, а в газету 2 рекламу вовсе не подавать.
. Следовательно, минимальный рекламный бюджет рекламодателя составит 18 у.е., если покупать 3 блока рекламы в газете 1 или устроенную площадь или рекламное место в газете в 3 раза выгоднее, а в газету 2 рекламу вовсе не подавать.
При таком решении достигается (в соответствии с используемым ограничениями) требуемая запоминаемость рекламы, но не удовлетворяется потребность в эмоциональности её восприятия.
С другой стороны два ограничивающих условия сами по себе также дают решение: из системы уравнений X 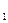 +2X
+2X 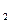 =3 и X
=3 и X 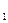 +4X
+4X 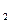 =4 мы получаем X
=4 мы получаем X 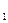 =2 X
=2 X 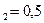 При этом решении удовлетворяются оба требования (в отношении запоминаемости и эмоциональности), но совершенно не принимается во внимание стоимость рекламы.
При этом решении удовлетворяются оба требования (в отношении запоминаемости и эмоциональности), но совершенно не принимается во внимание стоимость рекламы.
Если мы покупаем 2 рекламных блока или 2 площади в газете по 1и 0,5 блока в газете 2, удовлетворяется потребность в запоминаемости и эмоциональности рекламы, причем, стоимость рекламы будет минимальная, а именно 22,5 у.е.В решении этой задачи потребность в запоминаемости и эмоциональности рекламы удовлетворяются полностью.
Двойственна рассмотренной задаче задача на нахождение максимума целевой функции. Пусть из рекламных блоков газеты 1и2 необходимо составить характеристику запоминаемости и эмоциональности рекламы: Y 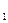 Y
Y 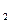 -наша оценка в у.е. полезности каждого из этих показателей. Общая (условная) оценка рекламного воздействия равна Y=3Y
-наша оценка в у.е. полезности каждого из этих показателей. Общая (условная) оценка рекламного воздействия равна Y=3Y 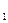 +4Y
+4Y 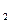 ; мы будем стремиться максимизировать Y.При этом стоимость 1 рекламного блока не может превышать его рыночной цены в газете 1- 6 у.е. и в газете 2-21 у.е.
; мы будем стремиться максимизировать Y.При этом стоимость 1 рекламного блока не может превышать его рыночной цены в газете 1- 6 у.е. и в газете 2-21 у.е.
Оценка полезности рекламного блока в газете 1 не может превышать 6 у.е., т.е. Y 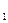 +Y
+Y 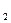
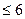 Аналогично для газеты 2 оценка воздействия рекламы равна Следовательно, двойственную задачу можно сформулировать таким образом: найти такие значения рекламного воздействия газетной рекламы, чтобы
Аналогично для газеты 2 оценка воздействия рекламы равна Следовательно, двойственную задачу можно сформулировать таким образом: найти такие значения рекламного воздействия газетной рекламы, чтобы
Y=3Y 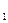 +4Y
+4Y 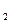
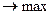 при условии
при условии
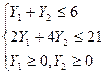
Связь между двумя задачами проста и легко распространяется на задачи линейного программирования. Обе двойственные задачи имеют одно и то же решение – в том смысле, что функции Z в первой задаче равен максимуму функции Y во второй задаче.
Решение задачи (1) следующее: X 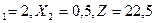 (минимальная стоимость рекламы в газете).Решение задачи (2): Y
(минимальная стоимость рекламы в газете).Решение задачи (2): Y 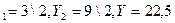 (максимальная оценка рекламного бюджета в газетах)
(максимальная оценка рекламного бюджета в газетах)
Далее рассмотрим игру с двумя участниками, платежная матрица которой –квадратная пятого порядка, построенная по данным задач 1 и 2.Где один участник-рекламодатель с желанием минимизации рекламных затрат, другой- рекламное агентство с желанием получить от рекламодателя как можно больший заказ на рекламу. Такая платежная матрица имеет вид:
A 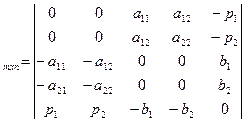
Нули объясняются тем, что игра справедлива(цена игры равна нулю). Поскольку матрица кососимметрична, оптимальной для обоих игроков является одна и та же смешанная стратегия Z=(Z1,Z2,Z3,Z4,Z5) Оптимальные стратегии Sm=(Z1,Z2,Z3,Z4,Z5) игры с платежной матрицей - A 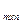 могут быть найдены путем решения симметричной пары двойственных задач линейного программирования. Тогда с учетом стратегий по подаче рекламы в газеты, система уравнений по матрице A
могут быть найдены путем решения симметричной пары двойственных задач линейного программирования. Тогда с учетом стратегий по подаче рекламы в газеты, система уравнений по матрице A  примет вид:
примет вид:
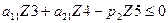
a 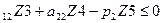
-a 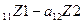 + b
+ b 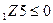
-a 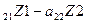 +b
+b 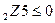
p 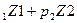 -b
-b 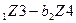 ≤ 0
≤ 0
Решение системы уравнений при данных из таблицы исходных значений параметров дает решение Z1=2, Z2=1\2,Z3=3\2,Z4=9\2 Значит, в решении системы должно соблюдаться соотношение стратегий:
Sm=(Z1:Z2:Z3:Z4:Z5)=(2:1\2:3\2:9\2:1)
Смысл значения Sm в следующем: для получения требуемой отдачи от рекламных вложений в газетах на единицу стратегии Z5 приходится две единицы стратегии Z1 (например, удвоенная публикация по площади в газете 1); 1\2 единицы Z2 (например, половина площади в газете 2);1,5 единицы Z3 (например, публикация в газете 1 только до уровня информационной насыщенности); 2,5 единицы Z4 (например, публикация в газете 2 до уровня только эмоциональной насыщенности)
Соотношение стратегий для решения стоящей проблемы через рекламные ассигнования должны быть в следующих объемах:
Q1=200 ед., Q2=50 ед., Q3=150 ед., Q4=450 ед., Q5=100ед.
Чтобы получить абсолютные значения Z, необходимо принять во внимание, что для абсолютных значений должно выполняться условие Z1+Z2=Z3+Z4=Z5=1 Нетрудно установить, что мы получили абсолютные величины Z, умножая на 2\19 элементы приведенного соотношения для оптимальных стратегий Sm. Следовательно, решением игры явится смешанная стратегия Sm=(4\19, 1\19,3\19,9\19,2\19), со всеми ранее выявленными соотношениями по рекламному ассигнованию и выбору места.
Таким образом, рассмотренная задача представляет собой стратегии рекламодателя –рекламного агентства (игра) или советы как поступиться с рекламным бюджетом предприятия для реализации (выигрыша) поставленной цели.
Пример 16
Оценка выбора рекламных стратегий.
На рекламном рынке происходит игра между рекламодателем (РД) и рекламным агентством (РА),которую можно формализовать матрицей рекламных платежей А 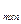 :
:
B 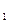 B
B 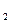 …. B
…. B 
………………………
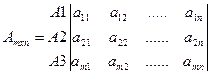
Где a  –выигрыш, а точнее, рекламные затраты, планируемые РА в ситуациях, когда РА выбрала рекламную стратегию А
–выигрыш, а точнее, рекламные затраты, планируемые РА в ситуациях, когда РА выбрала рекламную стратегию А  В общем случае у РА= (A1,A2,…,Am) Под рекламной стратегией может быть представлен выбираемый тип, вид рекламы, какие-то рекламные услуги, эффективность рекламной кампании, величина рекламного бюджета общие стратегии и т.п.
В общем случае у РА= (A1,A2,…,Am) Под рекламной стратегией может быть представлен выбираемый тип, вид рекламы, какие-то рекламные услуги, эффективность рекламной кампании, величина рекламного бюджета общие стратегии и т.п.
Стратегии РД= (B1,B2,…,Bn) -это признаки желательности (узнаваемость торговой марки, благоприятный образ, увеличение сбыта и т.д.) или общие стратегии рекламы в зависимости от жизненного цикла товара, ситуации на рынке и т.д., которые РД пытается получить от вложения своих средств в рекламу, представляемую в стратегиях Ai
Предположим, что значения a 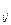 известны для каждой пары стратегий (Ai,Bj) Таким образом, матрица рекламных платежей характеризует состояния стратегий РД и РА, где a
известны для каждой пары стратегий (Ai,Bj) Таким образом, матрица рекламных платежей характеризует состояния стратегий РД и РА, где a 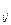 определяет выигрыш РА (получение заказы на рекламу) и выигрыша РД (увеличение издержек по рекламе) при применении стратегий (Ai,Bj).
определяет выигрыш РА (получение заказы на рекламу) и выигрыша РД (увеличение издержек по рекламе) при применении стратегий (Ai,Bj).
Цель РА- максимизировать заказы, цель РД- минимизировать рекламные затраты. В этом заключается смысл игры субъектов рекламного рынка
Пусть матрица А не содержит седловой точки, т.е. игра решается в смешанных стратегиях: S*1=(p 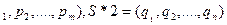 , где p
, где p 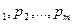 -вероятности использования РА стратегий A1,A2,…,A
-вероятности использования РА стратегий A1,A2,…,A 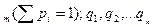 - вероятность использования РД рекламных стратегий B1,B2,…Bn(
- вероятность использования РД рекламных стратегий B1,B2,…Bn(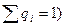 .
.
Таким образом, задача решения игры на рекламном рынке сводится к задаче линейного программирования. оптимальные стратегии S*1 S*2 с матрицей рекламных платежей A 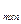 могут быть найдены путем решения симметричной пары двойственных задач линейного программирования:
могут быть найдены путем решения симметричной пары двойственных задач линейного программирования:

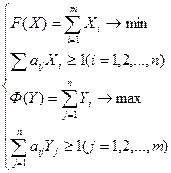
Решая их, находим значения X  Y
Y  цену
цену  игры и оптимальные стратегии S*1 S*2, где
игры и оптимальные стратегии S*1 S*2, где 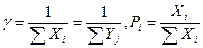 (i=1,2,…,m) q
(i=1,2,…,m) q 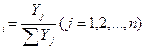
Рассмотрим следующий конкретный пример. Найти решение игры между РД и РА,исходя из значений рекламных платежей в тыс.руб. или у.е.
А= 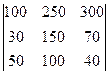
Постановка математической модели пары двойственных задач линейного программирования для матрицы А будет выглядеть так:
Найти минимум функции F(X)= X1+X2+X3 при ограничениях:
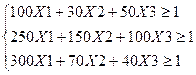
X 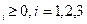
Решая систему уравнений (1) находим корни:X1= 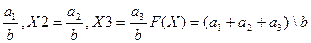 Из
Из 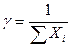 находим
находим 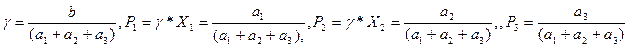 ,где a
,где a 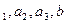 - числа из корней решения уравнения. Таким образом, оптимальная стратегия РА будет S*1=(
- числа из корней решения уравнения. Таким образом, оптимальная стратегия РА будет S*1=(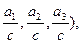 ,где с = a
,где с = a 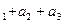
Задача нахождения оптимальной стратегии РД формулируется следующим образом:
Найти максимум функции F(Y)=Y 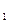 +Y
+Y 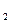 +Y
+Y 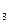 при ограничениях
при ограничениях
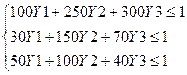
Y 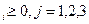
Так как Y 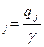 ,то сиcтему уравнений можно переписать так:
,то сиcтему уравнений можно переписать так:
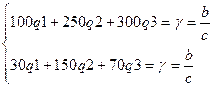
q 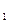 +q
+q 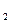 +q
+q 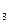 =1
=1