Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего значения, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.
Дисперсия случайной величины – мера разброса данной случайной величины, то есть её отклонения от математического ожидания.
Дисперсия простая:
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где 
– дисперсия; 
– i-й элемент выборки; 
– объём выборки; 
– среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Дисперсия взвешенная:
Более удобно вычислять дисперсию по формуле:
Данная формула получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для этого расчета нужны будут:
} n
xi –распределение ряда;
fi – абсолютные частоты, значение ряда;
wi – относительная частота, аналог вероятности или рассчитанная вместо fi;
n – количество объектов;
Произведем вычисления среднего квадрата отклонения:
Dx = 
= ∑ 
* 
∑wi = 1 или 100%
∑xwi = х среднее
∑ 
= х средний квадрат
Суммирование подразумевается по всем возможными «i». Дисперсия вычисляется в квадратных единицах. Средний квадрат и квадрат среднего это разные величины.
Очень редко случайная величина отклоняется от своего среднего значения больше чем на 3 сигма. Правило трёх сигм (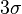
) – практически все значения нормально распределённой случайной величины лежат в интервале 
. Более строго - приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки).
Применение среднеквадратического отклонения:
- для суждения о колеблемости вариационных рядов и сравнительной оценки типичности (представительности) средних арифметических величин;
- для реконструкции вариационного ряда, т.е. восстановления его частотной характеристики на основе правила "трех сигм";
- для выявления "выскакивающих" вариант (при сопоставлении реального и реконструированного вариационных рядов);
- для расчета средней ошибки средней арифметической величины.
Коэффициент вариации (С) – это процентное отношение среднеквадратического отклонения к среднеарифметической величине:
С = σ / M x 100%.
Коэффициент вариации – это относительная мера колеблемости вариационного ряда.
Применение коэффициента вариации:
- сильное разнообразие ряда свидетельствует о малой представительности (типичности) соответствующей средней величины и, следовательно, о нецелесообразности ее использования в практических целях;
- для сравнительной оценки разнообразия (колеблемости) разноименных вариационных рядов и выявления более и менее стабильных признаков, что имеет значение в дифференциальной диагностике.