Распределение признака в совокупности изучают с помощью показателей асимметрии и эксцесса.
Используются основные формулы для оценки показателя асимметрии: коэффициенты асимметрии Пирсона, коэффициенты асимметрии Линдберга, коэффициент асимметрии на основе центрального момента третьего порядка.
О наличии асимметрии в распределении можно судить по таким показателям распределения как средняя арифметическая, мода и медиана. Разница между ними показывает наличие асимметрии ряда распределения. Формулы расчета коэффициента асимметрии Пирсона, использующие значения моды, дают приближенный результат:
,
где Мо – мода;
Для оценки распределения используют более точный метод центральных моментов, предложенный русским математиком П. Л. Чебышевым, которые рассчитываются аналогично пройденной уже ранее дисперсии, но поправляются на степень, в которую возводятся разницы 
.
Центральный момент первого порядка будет равен нулю. Разницы возводятся в первую степень , а согласно свойству средних их сумма будет равна нулю.
Второй центральный момент является дисперсией, так как рассчитанные разницы возводятся в квадрат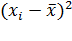 
.
Третий момент представляет собой еще одно умножение на заданную величину и поэтому имеет первоначальные положительные и отрицательные знаки, так как рассчитанные разницы возводятся в куб 
. Таким образом, третий момент и его знак зависит от преобладания положительных отклонений в кубе над отрицательными отклонениями либо наоборот. Центральный момент третьего порядка используется при оценке асимметрии.
Четвертый момент используется для оценки эксцесса 
. При его расчете разницы возводятся в четвертую степень. Эксцесс характеризует крутизну графика функции в сравнении с нормальным распределением при той же силе вариации.
Асимметрия – это показатель симметричности / скошенности кривой распределения, а эксцесс определяет ее островершинность.
где, 
– коэффициент асимметрии, 
–момент 3 порядка.
При нормальном и любом другом строго симметричном распределении сумма положительных отклонений в кубе строго равна сумме отрицательных отклонений в кубе.
Эксцесс. Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине.
где, 
– эксцесс, 
– момент 4 порядка.
Если у распределения 2 вершины (бимодальное распределение), то тогда эксцесс стремится к отрицательной величине. Нормальное распределение имеет величины асимметрии эксцесса равные нулю (см. рис.5.1).
Рис.5.1. Нормальное распределение, асимметрия и эксцесс
Распределение считается достоверно нормальным, если абсолютная величина показателей асимметрии и эксцесса меньше их ошибок репрезентативности в 3 и более раз.