Пример 3.1. Есть данные о статистике признака в трех группах.
| Xi1 | f(i)1 | Xi2 | f(i)2 | Xi3 | f(i)3 |
Найти эмпирический коэффициент детерминации.
Для расчета коэффициента детерминации 
необходимы межгрупповая, внутригрупповая и общая дисперсии.
Зная дисперсию общую и одну из двух других ее составляющих дисперсий (межгрупповая и внутригрупповая) можно найти коэффициент детерминации, значение которого не превышает единицу.
Произведем такую последовательность действий:
1) Для нахождения среднего значения рассчитываем столбцы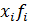 
для каждой группы. Для этого как уже указывали, в предыдущих примерах в электронной таблице Excel выбираем функцию ПРОИЗВЕД в категории "Математические" и указываем соответствующие ячейки;
2) Находим средние значения 
, 
в группах по известной также ранее формуле средней арифметической взвешенной:
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=" и после с помощью функции СУММ в категории "Математические" указываем столбец 
(числитель), ставим знак деления и после с помощью аналогичной функции выделяем столбец 
(знаменатель) данной группы. Аналогично находим ;
3) Рассчитываем столбец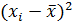 
для каждой группы данных, чтобы в последующем найти дисперсии в исследуемых группах.
В электронной таблице Excel выбираем функцию СТЕПЕНЬ в категории "Математические", после в первую графу указываем ячейки со значениями 
"минус" 
данной группы, а во второй графе "2";
4) Находим дисперсии по каждой группе по формуле:
Для этого в электронной таблице Excelв пустой ячейке ставим знак "=", после выбираем функцию СУММПРОИЗВ в категории "Математические" и указываем столбцы 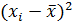и (числитель), а после ставим знак деления и с помощью функции СУММ в скобках после этого знака указываем столбец 
. Аналогично находим дисперсии других групп 
и 
;
5) Рассчитываем 
общую среднюю всей совокупности по формуле, используя средние значения каждой группы входящей в эту совокупность:
В электронной таблице Excelв пустой ячейке ставим знак "=", после, используя функцию СУММПРОИЗВ, в первом массиве указываем все ячейки со средними значениями, а во второй – суммы столбцов по каждой группе (числитель), ставим знак деления, после, используя функцию СУММ, указываем все суммы столбцов 
;
6) Находим межгрупповую дисперсию по формуле:
Для этого в электронной таблице Excel рассчитываются значения 
по операциям, описанным в третьем действии, после в пустой ячейке ставим знак "=" и, используя функцию СУММПРОИЗВ, указываем в первом массиве значения , а во втором массиве – значения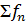 
(числитель). Далее ставим знак деления и, используя функцию СУММ, указываем все значения 
7) Определяем внутригрупповую дисперсию по формуле:
В электронной таблице Excelв пустой ячейке ставим знак "=", после, используя функцию СУММПРОИЗВ, указываем в первом массиве значения дисперсий по группам, а во втором – суммы значений 
(числитель), после ставим знак деления и, с помощью функции СУММ, указываем все значения 
;
8) Находим общую дисперсию по формуле:
9) Определяем эмпирический коэффициент детерминации по формуле:
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после указываем ячейку со значением межгрупповой дисперсией, ставим знак деления и указываем ячейку со значением общей дисперсии.
На основе проведённых расчетов получены следующие результаты (см. рис. 3.1).
Рис.3.1. Результаты расчета эмпирического коэффициента детерминации
Вопросы и задачи к теме
Вопросы для изучения
1. Межгрупповая и внутригрупповая дисперсии.
2. Общая дисперсия.
3. Частная групповая дисперсия.
4. Коэффициент детерминации.
5. Эмпирическое корреляционное соотношение.
6. Сложение дисперсий для доли признака.