Задача 7.1. Заданы пары значений бинарного признака.
| ДА | НЕТ | |
| ДА | ||
| НЕТ |
Найти значение коэффициента Фехнера
Задача 7.2. Заданы пары значений бинарного признака.
| ДА | НЕТ | |
| ДА | ||
| НЕТ |
Найти значение коэффициента Фехнера и фи квадрат.
ТЕМА 8. ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПРИЗНАКАМИ. КОРРЕЛЯЦИОННАЯ СВЯЗЬ
Основные теоретические сведения темы
Существует 2 вида связи между отдельными признаками: функциональная и стохастическая (статистическая), частным случаем которой является корреляционная.
Корреляционная связь – связь, проявляющаяся не в каждом отдельном случае, а в массе случаев в средних величинах в форме тенденции.
Статистическое исследование корреляционной связи ставит своей конечной целью получение модели зависимости для ее практического использования.
Изучение корреляционных связей сводится в основном к решению следующих задач:
1) выявление наличия (отсутствия) корреляционной связи между изучаемыми признаками;
2) измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов (эта часть исследования именуется корреляционным анализом);
3) определение уравнения регрессии – математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных – факторных признаков (эта часть исследования именуется регрессионным анализом).
Статистическое исследование корреляционной связи ставит своей конечной целью получение модели зависимости для ее практического использования.
Важно понимать, что корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях.
Для нахождения коэффициента линейной корреляции можно воспользоваться формулой
- коэффициент линейной корреляции;
– значения одноименных столбцов;
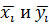– средние арифметические значения одноименных столбцов.
Также можно воспользоваться сокращенным видом
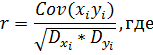
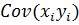– ковариация значений;
– дисперсии одноименных значений.
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rt,t-1 < 0.3: слабая;
0.3 < rt,t-1 < 0.5: умеренная;
0.5 < rt,t-1 < 0.7: заметная;
0.7 < rt,t-1 < 0.9: высокая;
0.9 < rt,t-1 < 1: весьма высокая;
В нашем примере связь между рядами - высокая и прямая.
При положительной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному увеличению (или уменьшению) другой переменной т.е. взаимосвязи типа увеличение-увеличение (уменьшение-уменьшение).
При отрицательной корреляции увеличение (или уменьшение) значения одной переменной ведет к закономерному уменьшению (или увеличению) другой переменной т.е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).
Способы представления корреляционной связи
–график (диаграмма рассеяния);
–коэффициент корреляции.