Пример 11.1. Даны показатели товарооборота по месяцам
| Месяцы | Июнь | Июль | Август | Сентябрь | Октябрь |
| Объем продаж млн рублей | 3,7 | 6,7 | 8,1 | 9,9 | |
| Темп роста (цепной) | 1,351351 | 1,34 | 1,208955 | 1,222222 | |
| Темп роста (базисный) | 1,2 | 1,57 | 1,68 | 1,8 |
Найти среднемесячный темп роста объема продаж торговой организации.
Рассчитаем темп роста:
*100%-100%= 
*100%-100%=49,38%
где 
– темп прироста цепной.
Рис.11.1. Результаты расчета темпа роста
Пример 11.2. Имеются следующие данные
| Год | 2010-2015 | |
| Введение в эксплуатацию площади уi | 70,5 | 415,7 |
Определить среднегодовой темп роста в млн. руб. за 2010-2015гг. (т. е за 6 лет), потреблено за период на 415,7 млн. руб.
Используем формулу средней параболической:
В нашем примере y0 = 70,5, а 
= 415,7 т. е отношение
= 
= 5,896
В случае отсутствия подручных средств техники для получения результата можно воспользоваться статистическими таблицами в приложении. В графе n = 6 находим значение, наиболее близкое к полученному отношению (5,896). Это число 5,914, которому соответствует 
= 1,115. Это и есть среднегодовой коэффициент роста за 6 лет (с 2010-2015 г.). Итак, среднегодовой темп роста за указанный период составлял 111,5%, а среднегодовой темп прироста был равен 111,5% - 100% = 11,5 %.
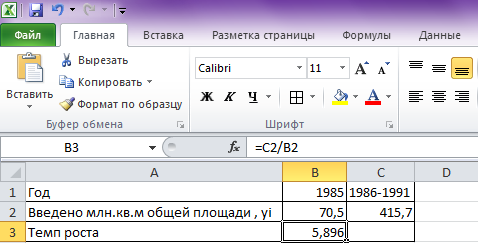
Рис.11.2. Результаты расчета темпа роста.
Для того чтобы сделать это в электронной таблице Excel необходимо выполнить следующие действия:
1. Ввести в ячейки необходимые числа.
2. Ввести формулу в ячейку такую же, как указанно на рисунке выше.
Далее можно воспользоваться статистическими таблицами в приложении.
Пример 11.3. Задан вариационный ряд.
| X | ||||||||||||
| Y |
Найти январский индекс сезонности относительно регрессии: 
Для нахождения январского индекса сезонности необходимо найти теоретическое значение Y
Произведём такую последовательность действий:
1) Рассчитаем столбец 
для нахождения ковариации путём умножения значений. Для этого в электронной таблице Excel выбираем функцию ПРОИЗВЕД в категории "Математические" и выделяем соответствующие ячейки;
2) Рассчитаем столбцы 
для нахождения дисперсии путём возведения значений в квадрат. Для того чтобы сделать это в электронной таблице Excel выбираем функцию СТЕПЕНЬ в категории "Математические", указав ячейку со значением, которое надо возвести в степень, в графе "Степень" пишем "2";
3) Находим средние значения столбцов 
по формуле средней арифметической. Таким образом, получим средние значения 
4) Рассчитываем ковариацию по сокращенной формуле:
В Excelдля нахождения ковариации можно использовать функцию КОВАР в категории "Статистические", обозначив нужные столбцы;
5) Находим дисперсии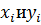 
по сокращенной формуле:
В Excel используем функцию ДИСПР в категории "Статистические", обозначив нужные ячейки;
6) Рассчитаем коэффициент 
по сокращенной формуле:
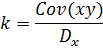
В электронной таблице Excel в пустой ячейке ставим знак "=", после указываем ячейку со значением ковариации, ставим знак деления и указываем ячейку со значением дисперсии;
7) Найдём коэффициент 
по формуле:
ВExcel для быстрого нахождения этих коэффициентов можно воспользоваться функцией ЛИНЕЙН в категории "Статистические", указывая на необходимые данные и вводить как массив, используя клавиши CTRL + SHIFT + ENTER, выделив 2 ячейки по горизонтали;
8) Рассчитываем теоретические значения для нахождения остатков по формуле:
– теоретические значения; 
– значения из столбца Х; 
– коэффициенты линейной регрессии.
В электронной таблице Excel в пустой ячейке ставим знак "=", после, используя функцию ПРОИЗВЕД, указываем ячейки со значениями 
, ставим знак "плюс", а потом указываем ячейку со значением ;
9) Найдём январский индекс сезонности по формуле:
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после указываем ячейку с первым фактическим значением Y, ставим знак деления, а после указываем ячейку с теоретическим значением Y.
На основе проведённых расчетов получены следующие результаты (см. рис.11.3)
Рис.11.3. Результаты расчета январского индекса сезонности
Пример 11.3. Задан вариационный ряд.
| X | ||||||||||||
| Y |
Определить автокорреляцию значения 
с его предыдущим значением 
.
Для нахождения коэффициента автокорреляции можно воспользоваться формулой
Также можно воспользоваться, как указывалось ранее сокращенным видом формулы корреляции с небольшими поправками
– ковариация значений;
– дисперсии одноименных значений.
Произведём такую последовательность действий:
1) Для нахождения коэффициента автокорреляции сделаем два столбика 
, где в первый вписываем все значения, начиная со второго, а во второй – все значения кроме последнего.
2) Рассчитаем столбец 
для нахождения ковариации путём умножения значений.
Для этого в электронной таблице Excel выбираем функцию ПРОИЗВЕД в категории "Математические" и выделяем соответствующие ячейки;
3) Рассчитаем столбцы 
для нахождения дисперсии путём возведения значений в квадрат.
Для того чтобы сделать это в электронной таблице Excel выбираем функцию СТЕПЕНЬ в категории "Математические", указав ячейку со значением, которое надо возвести в степень, в графе "Степень" пишем "2";
4) Находим средние значения столбцов 
для нахождения ковариации и дисперсий по формуле средней арифметической:
– среднее значение; 
– значения из столбца ; 
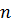– количество значений.
Для этого в электронной таблице Excel выбираем формулу СРЗНАЧ в категории "Статистические" и выделяем необходимые ячейки. Аналогично получаем средние значения значений 
;
5) Рассчитываем ковариацию по сокращенной формуле:
В электронной таблице Excel в пустой ячейке ставим знак "=", после чего указываем ячейку со значением 
, ставим "минус" и, с помощью функции ПРОИЗВЕД, умножаем ячейки со значениями 
, указывая их в скобках;
6) Находим дисперсии 
по сокращенной формуле:
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после чего указываем ячейку со значением 
, после ставим знак "минус" и указываем ячейку со значением возведённым в квадрат аналогично действиям, описанным в третьем действии. Аналогично находим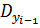 
или можно использовать функцию ДИСПР в категории "Статистические", обозначив нужные ячейки;
7) Находим коэффициент автокорреляции по формуле:
В электронной таблице Excel в пустой ячейке ставим знак "=" и, используя знак деления, формулы КОРЕНЬ и ПРОИЗВЕД, а, также, соответствующие ячейки, печатаем эту формулу (пример: =B23/КОРЕНЬ(ПРОИЗВЕД(B24;B25)), где В23 – ячейка со значением ковариации; В24 и В25 – ячейки со значениями дисперсий).
На основе проведённых расчетов получены следующие результаты (см. рис.11.4)
Рис.11.4. Результаты расчета коэффициента автокорреляции
Пример 11.4. Задан вариационный ряд.
| X | ||||||||||||
| Y |
Сделать измерение сезонных колебаний
С целью усвоения пройденного материала выполняем действия, описанные в задании ранее, но в последнем 9 действии находим индекс для каждого месяца.
Произведём уже знакомую последовательность действий:
1) Рассчитаем столбец для нахождения ковариации путём умножения значений. Для этого в электронной таблице Excel выбираем функцию ПРОИЗВЕД в категории "Математические" и выделяем соответствующие ячейки;
2) Рассчитаем столбцы для нахождения дисперсии путём возведения значений в квадрат;
3) Находим средние значения столбцов 
по формуле средней арифметической. Таким образом, получим средние значения 
4) Рассчитываем ковариацию по сокращенной формуле:
ВExcelдля нахождения ковариации можно использовать функцию КОВАР в категории "Статистические", обозначив нужные столбцы;
5) Находим дисперсии 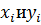по сокращенной формуле:
ВExcel используем функцию ДИСПР в категории "Статистические", обозначив нужные ячейки;
6) Рассчитаем коэффициент по сокращенной формуле:
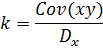
7) Найдём коэффициент по формуле:
8) Рассчитываем теоретические значения по формуле:
9) Найдём индексы сезонности:
На основе проведённых расчетов получены следующие результаты (см. рис.11.5)
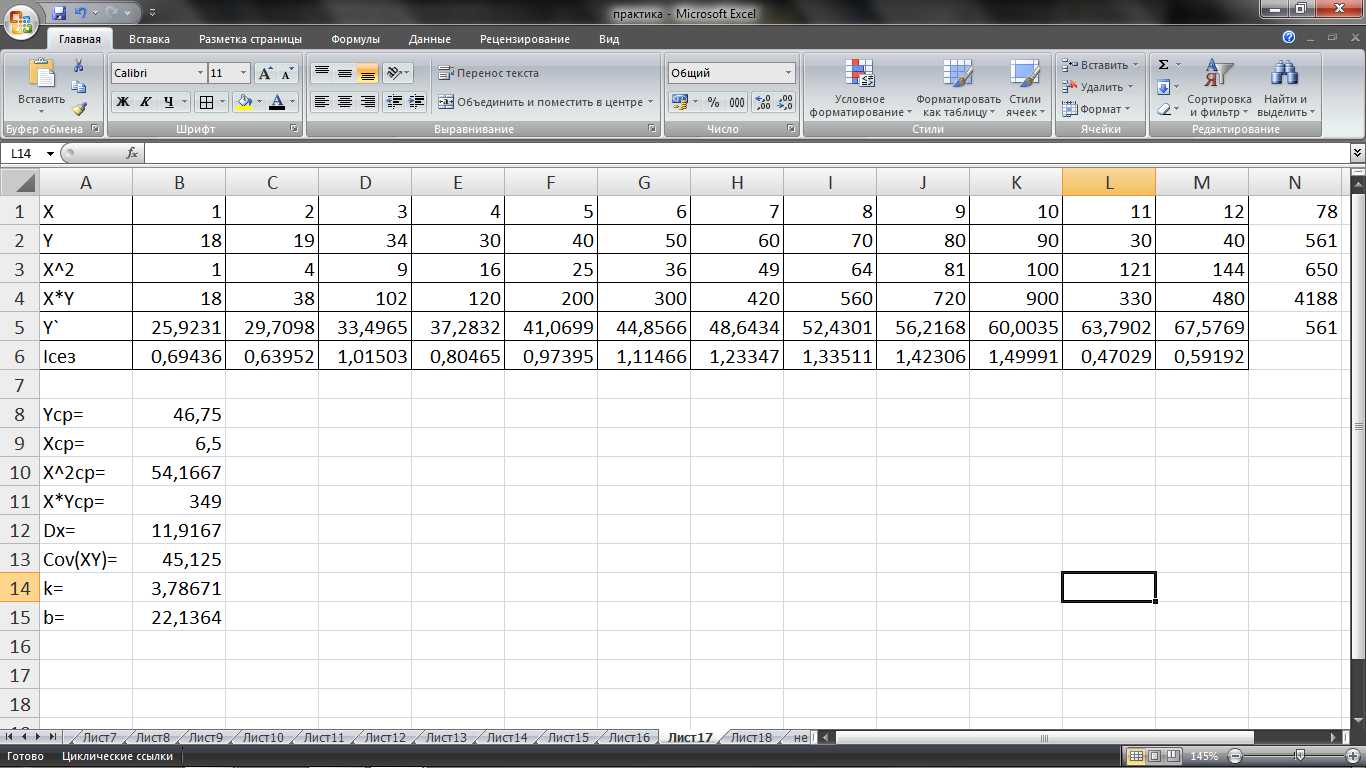
Рис.11.5. Результаты расчетов сезонных колебаний
Пример 11.6. Задан вариационный ряд.
| X | ||||||||||||
| Y |
Найти коэффициент автокорреляции, автокорреляцию в остатках, критерий Дарбина–Уотсона.
Произведём уже знакомую последовательность действий:
1) Для нахождения коэффициента автокорреляции сделаем два столбика 
, где в первый вписываем все значения, начиная со второго, а во второй – все значения кроме последнего.
2) Рассчитаем столбец для нахождения ковариации путём умножения значений;
3) Рассчитаем столбцы 
для нахождения дисперсии путём возведения значений в квадрат;
4) Находим средние значения столбцов 
для нахождения ковариации и дисперсий по формуле средней арифметической:
5) Рассчитываем ковариацию по сокращенной формуле:
6) Находим дисперсии по сокращенной формуле:
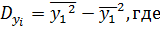
7) Находим коэффициент автокорреляции по формуле:
На основе проведённых расчетов получены следующие результаты (см. рис.11.6).
Рис.11.6. Результаты расчета коэффициента автокорреляции
После нахождения коэффициента найдём критерий Дарбина-Уотсона следующей последовательностью действий:
8) Находим 
, рассматривая первоначальные данные, для нахождения коэффициентов линейной регрессии вида 
;
9) Рассчитаем коэффициент по формуле:
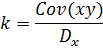
10) Найдём коэффициент по формуле:
11) Рассчитываем теоретические значения для нахождения остатков по формуле:
12) Рассчитываем остатки по формуле:
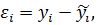
– остатки; – фактические значения; 
– ожидаемые значения.
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после указываем на ячейку со значением , ставим знак "минус", а после указываем на соответствующую ячейку со значением ;
13) Рассчитываем столбец 
путём отнимания от текущего значения остатка предыдущее значение.
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после указываем ячейку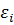 
(кроме первой т.к. предыдущего значения она не имеет), ставим знак "минус", а после указываем предыдущую ячейку значения ;
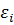14) Рассчитываем столбцы 
и 
для нахождения критерия Дарбина-Уотсона.
15) Находим критерий Дарбина-Уотсона по формуле:
В электронной таблице Excel в пустой ячейке ставим знак "=", после, используя функцию СУММ в категории "Статистические", указываем столбец , ставим знак деления, а после, используя функцию СУММ, указываем столбец .
Для более быстрого нахождения значени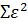й 
и 
можно воспользоваться функцией СУММКВ в категории "Статистические", указав в скобках значения столбцов 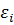и соответственно.
На основе проведённых расчетов получены следующие результаты (см. рис.11.7).
Рис.11.7. Результаты расчетов критерия Дарбина-Уотсона
16) Рассчитываем аналогично выполненным в 1-7 действии операциям, только беря за основу данных столбец 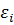. Посредством чего находим коэффициент автокорреляции в остатках.
На основе проведённых расчетов получены следующие результаты (см. рис. 11.8).
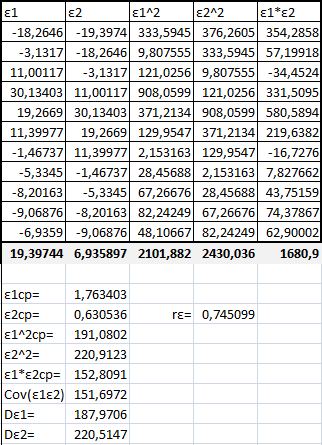
Рис.11.8. Результаты расчета коэффициента автокорреляции в остатках.
Вопросы и задачи к теме
Вопросы для изучения
1. Измерение колеблемости.
2. Выявление сезонных колебаний. Измерение сезонных колебаний.
3. Среднее квадратичное отклонение индексов сезонности и их коэффициент вариации.
4. Расчёт индексов сезонности за ряд лет. Прогнозирование с учётом индекса сезонности.
5. Коэффициент автокорреляции. Автокорреляция в остатках.
6. Критерий Дарбина–Уотсона.
7. Уравнение авторегрессии и нахождение его коэффициентов.