Пример 10.1. Задан вариационный ряд.
| X | ||||||||||||
| Y |
Найти коэффициенты уравнения линейной регрессии: 
Для нахождения значений коэффициентов уравнения линейной регрессии нам необходимо вычислить ковариацию, дисперсию независимого значения и средние значения. Зная средние значения, дисперсию и ковариацию можно найти коэффициенты уравнения
Произведём такую последовательность действий, при которой значительная часть процедуры уже известна из предыдущего задания:
1) Рассчитаем столбец 
для нахождения ковариации путём умножения значений. Для этого в электронной таблице Excel выбираем функцию ПРОИЗВЕД в категории "Математические" и выделяем соответствующие ячейки;
2) Рассчитаем столбцы 
для нахождения дисперсии путём возведения значений в квадрат. Для того чтобы сделать это в электронной таблице Excel выбираем функцию СТЕПЕНЬ в категории "Математические", указав ячейку со значением, которое надо возвести в степень, в графе "Степень" пишем "2";
3) Находим средние значения столбцов 
по формуле средней арифметической. Таким образом, получим средние значения 
4) Рассчитываем ковариацию по сокращенной формуле:
В Excel для нахождения ковариации можно использовать функцию КОВАР в категории "Статистические", обозначив нужные столбцы;
5) Находим дисперсии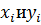 
по сокращенной формуле:
В Excel используем функцию ДИСПР в категории "Статистические", обозначив нужные ячейки;
6) Можно дальше найти коэффициент линейной корреляции, по сокращенной формуле подставляя полученные значения и произвести более длинный расчет значения 
, но как ране указано будет использоваться также сокращенная формула его расчета:
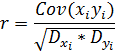
Рассчитаем коэффициент по сокращенной формуле:
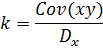
В электронной таблице Excel в пустой ячейке ставим знак "=", после указываем ячейку со значением ковариации, ставим знак деления и указываем ячейку со значением дисперсии;
7) Найдём коэффициент 
по формуле:
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после указываем ячейку со значением 
, ставим знак "минус" и, используя функцию ПРОИЗВЕД, указываем ячейки со значениями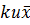 
в скобках.
На основе проведённых расчетов получены следующие результаты (см. рис.10.1).
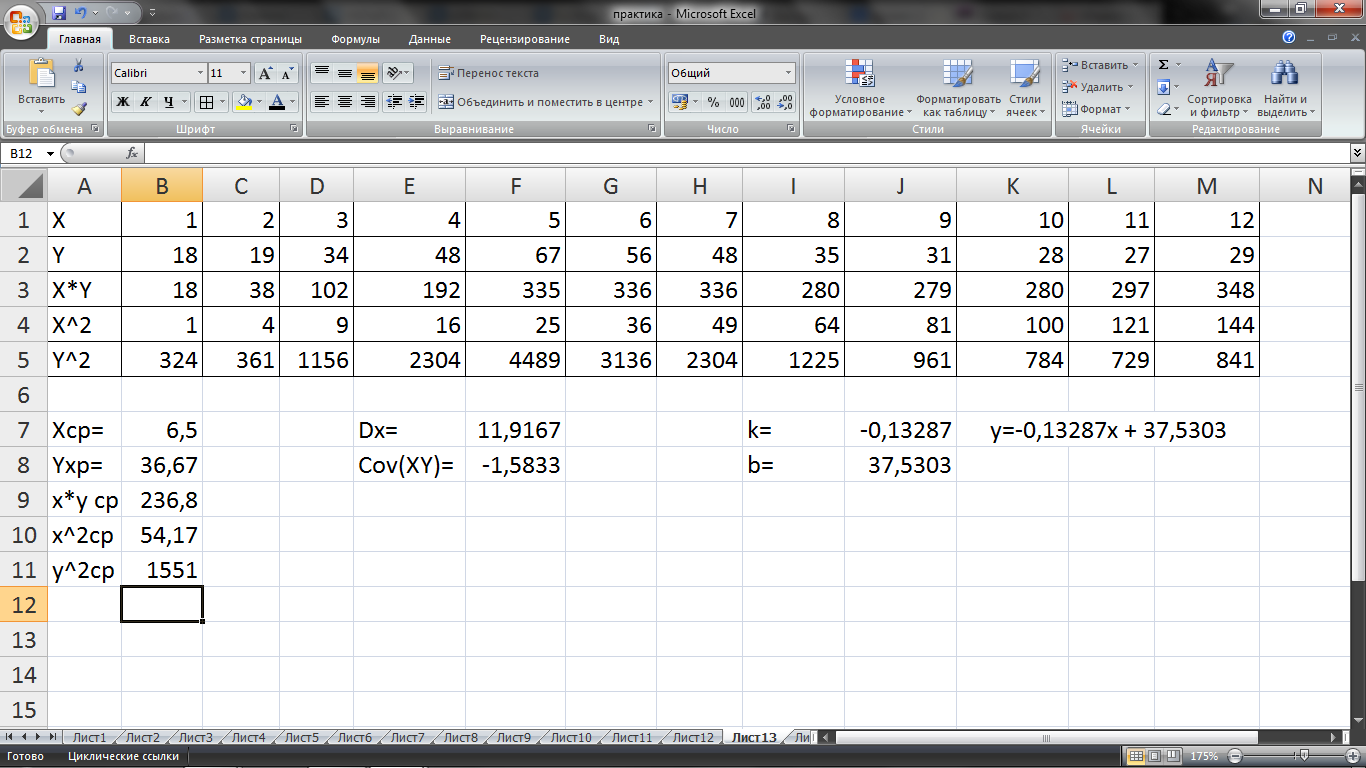
Рис.10.1. Результаты расчета коэффициентов линейной регрессии
Также в Excel для быстрого нахождения этих коэффициентов можно воспользоваться функцией ЛИНЕЙН в категории "Статистические", указывая на необходимые данные и вводить как массив, используя клавиши CTRL + SHIFT + ENTER, выделив 2 ячейки по горизонтали;
Вопросы и задачи к теме
Вопросы для изучения
1. Эмпирическая линия регрессии. Эмпирическое корреляционное соотношение.
2. Линейный коэффициент корреляции.
3. Проверка коэффициента корреляции на значимость (существенность).
4. Парная линейная регрессия, расчёт её параметров.
5. Остаточная дисперсия. Остаточное среднее квадратичное уравнение.
6. Сопряжённые уравнения.