Пример 8.1. Даны значения величин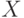 
и 
.
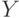| X | ||||||||||
| Y |
Найти коэффициент линейной корреляции.
Произведём такую последовательность действий:
1) Рассчитаем столбец 
для нахождения ковариации путём умножения значений. Для этого в электронной таблице Excel выбираем функцию ПРОИЗВЕД в категории "Математические" и выделяем соответствующие ячейки;
2) Рассчитаем столбцы 
для нахождения дисперсии путём возведения значений в квадрат. Для того чтобы сделать это в электронной таблице Excel выбираем функцию СТЕПЕНЬ в категории "Математические", указав ячейку со значением, которое надо возвести в степень, в графе "Степень" пишем "2";
3) Находим средние значения столбцов 
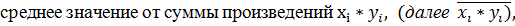по формуле средней арифметической:
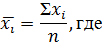
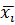– среднее значение; 
– значения из столбца ; 
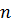– количество значений.
В электронной таблице Excel вопрос формулы вида средней решается программой самостоятельно, а Мы только выбираем формулу СРЗНАЧ в категории "Статистические" и выделяем необходимые ячейки. Таким образом, получаем средние значения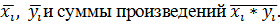 
4) Рассчитываем ковариацию по сокращенной формуле:
В электронной таблице Excelв пустой ячейке ставим знак "=", после чего указываем ячейку со значением среднего произведения 
и ставим "минус" произведение средних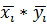 
. Произведение средних получаем с помощью функции ПРОИЗВЕД, умножая ячейки со значениями 
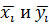,указывая их в скобках.
Также в Excel для более быстрого и эффективного нахождения ковариации можно использовать функцию КОВАР в категории "Статистические", обозначив нужные столбцы;
5) Находим дисперсии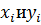 
по сокращенной формуле:
|
|
– квадрат среднего.
Для этого в электронной таблице Excel в пустой ячейке ставим знак "=", после чего указываем ячейку со значением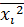 
, после ставим знак "минус" и указываем ячейку со значением, 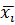возведённым в квадрат. Аналогично находим 
.
Также в Excel как уже отмечалось, что для более быстрого и эффективного нахождения дисперсии можно использовать функцию ДИСПР в категории "Статистические", обозначив нужные ячейки;
6) Находим коэффициент линейной корреляции, по сокращенной формуле подставляя полученные значения:
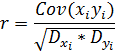
В электронной таблице Excel в пустой ячейке ставим знак "=" и, используя знак деления, формулы КОРЕНЬ и ПРОИЗВЕД, получаем значение коэффициента.
Пример:=B19/КОРЕНЬ(ПРОИЗВЕД(B16;B17)), где В19 – ячейка со значением ковариации; В16 и В17 – ячейки со значениями дисперсий).
Результаты представлены на рисунке 8.1.
Пример 8.2. Заданы пары значений Х и Y.
| X | ||||||||||
| Y |
Найти коэффициент линейной корреляции.
Используем коэффициент линейной корреляции, рассчитываемый по сокращенной формуле подставляя значения которые находятся как в предыдущей задаче:
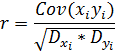
Для более быстрого нахождения коэффициента в Excel можно использовать функции PEARSON или КОРРЕЛ в категории "Статистические", указав необходимые столбцы.
На основе проведённых расчетов получены следующие результаты (см. рис. 8.1).
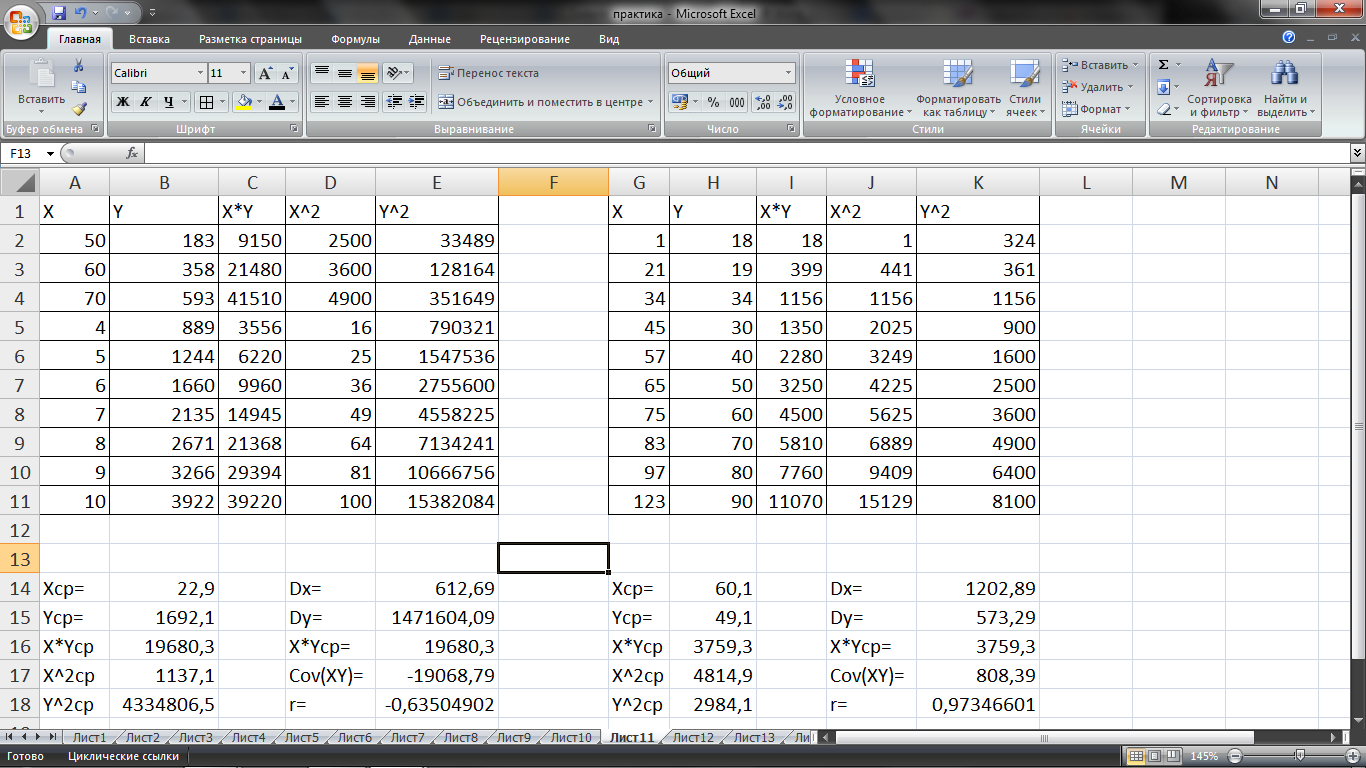
Рис.8.1.Результаты расчета коэффициента линейной корреляции
Вопросы и задачи к теме
Вопросы для изучения
|
|
1. Корреляционный анализ.
2. Регрессионный анализ.
3. Методы выявления корреляционной связи. Коэффициент Фехнера.
4. Метод группировок. Корреляционная таблица.
5. Эмпирическое корреляционное соотношение.
6. Линейный коэффициент корреляции.
7. Проверка коэффициента корреляции на значимость (существенность).