Пример 14.1. В 120 туристических агентствах предполагается провести методом механического отбора обследование среднемесячного количества реализованных путевок. Определить численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 5 путевок. Дисперсия пробного обследования составляет 250.
По формуле определяем численность выборки при механическом отборе:

Необходимый объем выборки определяется:

Таким образом, чтобы с данной точностью определить среднемесячное количество реализованных путевок, необходимо отобрать 9,23 туристических агентств (см. рис. 14.1).

Рис. 14.1. Результаты расчета численности выборки
Пример 14.2. Планируется проведение выборочного обследования на предприятии, где работает 230 бригад рабочих. Необходимо определить удельный вес рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 245.Определить с вероятностью 0,683 необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Находим необходимое количество бригад на основе формулы объема серийной бесповторной выборки:
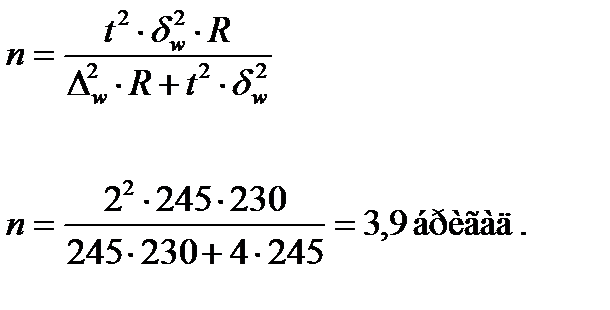
Чтобы сделать это в электронной таблице Excel, необходимо выполнить следующие действия: ввести в ячейки необходимые числа, ввести формулу в ячейку такую же, как указанно на рисунке выше.
Таким образом, чтобы с заданной точностью определить удельный вес рабочих, имеющих профессиональные заболевания, необходимо из 230 бригад обследовать 3,9 бригад (см. рис. 14.2).
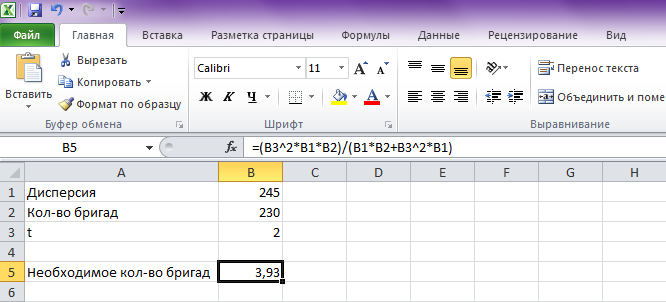
Рис. 14.2. Результаты расчета выборки
Пример 14.3. При проверке веса импортируемого груза на таможне методом случайной повторной выборки отобрано 210 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. Необходимо определить c вероятностью 0,9973 пределы, в которых находится средний вес изделий в генеральной совокупности.
Рассчитаем предельную ошибку выборки. Так, при Р =0,9973, t =3 (см. рис. 14.3).


Рис. 14.3. Расчет выборки
Для того чтобы сделать это в электронной таблице Excel необходимо выполнить следующие действия: ввести в ячейки необходимые числа; ввести формулу в ячейку такую же, как указанно на рисунке выше.
(В ячейке D1 указан корень из 210, для удобства расчетов) Определим пределы генеральной средней:
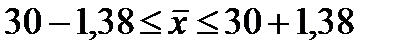 или
или 
Следовательно, с вероятностью 0,9973 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 28,62 до 31,38 г.
Пример 14.4. Методом случайной повторной выборки в отделении связи планируется определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Необходимо определить численность выборки, если результаты выборки необходимо дать с точностью до 1% и с вероятностью 0,95.
Известны размер предельной ошибки - Dw = 0,01, принята вероятность – Р = 0,95, t=1,96;
Необходимая численность выборки при случайном повторном отборе будем находить по формуле:

Значение w не дано по условию, поэтому следует ориентироваться на дисперсию, которой соответствует значение w = 0,5.
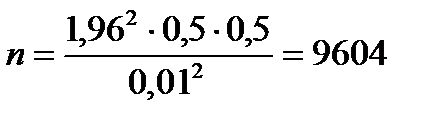
Представим расчет формулы в электронной таблице (см. рис. 14.4).

Рис. 14.4. Результаты расчета выборки
Таким образом, чтобы с данной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной повторной выборки отобрать 9604 письма.
Пример 14.5. В 100 туристических агентствах предполагается провести методом механического отбора обследование среднемесячного количества реализованных путевок. Определить численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок. Дисперсия пробного обследования составляет 225.
Так как отбор механический, численность выборки определяется по формуле:

Рассчитаем необходимый объем выборки:

Представим расчет формулы в электронной таблице (см. рис. 14.5).

Рис. 14.5. Результаты расчета численности выборки.
Таким образом, чтобы с данной точностью определить среднемесячное количество реализованных путевок, необходимо отобрать 20 туристических агентств.
Пример 14.6. Планируется проведение выборочного обследования на предприятии, где работает 200 бригад рабочих. Необходимо определить удельный вес рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225.Определить с вероятностью 0,683 необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
 Рассчитаем необходимое количество бригад на основе формулы объема серийной бесповторной выборки:
Рассчитаем необходимое количество бригад на основе формулы объема серийной бесповторной выборки:
Представим расчет формулы в электронной таблице (см. рис. 14.6).
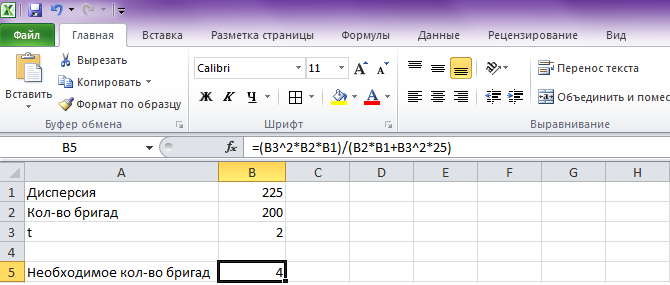
Рис. 14.6. Результаты расчета выборки
Таким образом, чтобы с заданной точностью определить удельный вес рабочих, имеющих профессиональные заболевания, необходимо из 200 бригад обследовать 4 бригады.
Пример 14.7. При механическом способе отбора из партии готовых изделий в 20 000 единиц было обследовано 800 единиц. В числе обследованных изделий 640 были отнесены к высшему сорту. Определить какой процент изделий высшего сорта во всей партии с вероятностью 0,9973 возможный.
В случае механического отбора предельная ошибка определяется по следующей формуле:

Границы генеральной доли изделий высшего сорта:


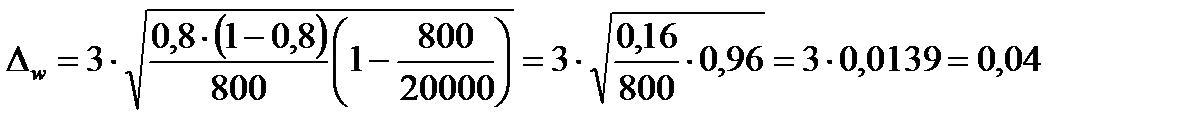

Следовательно, генеральная доля находится в пределах:

В Excel для удобства делим уравнение под корнем на две части. Первая часть состоит из w. Далее в ячейку E1 вписываем числитель первой части B5*(1-B5), а знаменатель оставляем не тронутым. Во второй части уравнения вписываем в ячейку E2, 1-(B2/B1). Далее мы получаем числа под корнем (смотрите формулу в решении выше). После чего делим ячейку E1 на 800 (ячейка B2) и умножаем все на ячейку E2. Далее извлекаем корень из полученного числа (как показанно на рисунке). После этого полученное число умножаем на t (3) и получаем ответ (E4*B4). Представим расчет формул в электронной таблице (см. рис. 14.7).

Рис. 14.7. Расчет процента изделий высшего сорта
Таким образом, с вероятностью 0,9973 можно утверждать, что во всей партии от 76 до 84 % – продукция высшего сорта.
Пример 14.8. При обследовании 100 образцов изделий, отобранных из партии в случайном порядке, оказалось 20 нестандартных. Определить с вероятностью 0,954 пределы, в которых находится доля нестандартной продукции в партии.
Чтобы определить границы генеральной доли, необходимо определить выборочную долю и ошибку выборочной доли.
Рассчитаем долю нестандартной продукции в выборочной совокупности:

Предельная ошибка выборочной доли с вероятностью 0,954 составит:

Доля нестандартной продукции в генеральной совокупности определяется по формуле:

Представим расчет формул в электронной таблице (см. рис. 14.8).

Рис. 14.8. Расчеты доли нестандартной продукции.
Таким образом, с вероятностью 0,954 можно утверждать, что доля нестандартной продукции в партии товара находится в пределах от 12 до 28%.
Пример 14.9. В городе 500 тыс. жителей. Методом случайного бесповторного отбора была обследована десятая часть жителей. В результате было установлено, что в городе 15% жителей старше 60 лет. Определить с вероятностью 0,683 пределы, в которых находится доля жителей в городе в возрасте старше 60 лет.
Доверительные интервалы для доли в генеральной совокупности определяются:

По условию задачи, выборочная доля w = 15% (или w = 0,15).
С вероятностью 0,683 определим предельную ошибку выборки для доли альтернативного признака:
 Определяем доверительные интервалы
Определяем доверительные интервалы
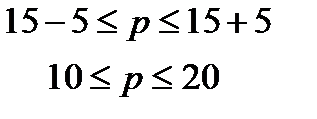
Таким образом, с вероятностью 0,683 можно утверждать, что доля жителей в возрасте старше 60 лет в городе А находятся в пределах 10% £ р £ 20%.
Представим результаты в электронной таблице (рис. 14.9).

Рис. 14.9. Расчет доли жителей старше 60 лет
Вопросы и задачи к теме
Вопросы для изучения
1. Генеральная совокупность и выборка из нее.
2. Основные способы организации выборки.
3. Статистическая совокупность.
4. Основные характеристики параметров генеральной и выборочной совокупности.
5. Ошибки выборки.
6. Распространение выборочных результатов на генеральную совокупность.
7. Необходимый объем выборки.