Инвестиционный портфель – это совокупность различных комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска. Портфель может быть технически составлен для любых видов финансовых инструментов и активов: акций, облигаций, фьючерсов, индексов, недвижимости и т.д.
В основе модели Марковица лежат два ключевых показателя любого финансового инструмента: доходность и риск. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.
Модель позволяет снизить систематические риски за счет группировки активов с отрицательной корреляцией доходностей.
Пусть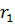 
– средняя доходность за определенный отрезок времени (предыдущий). Как рекомендуют классики, нужно смотреть в прошлое на лет 7-10, т.е. 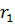– усреднение доходности ценных бумаг за период ... 
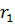. Доходность измеряется в процентах, а что касается дисперсии, то она измеряется в квадратных процентах и обозначается 
… 
. Вместо дисперсии можно использовать среднеквадратическое отклонение 
… 
.
Так же необходимо знать ковариацию каждой бумаги с остальными 
, для всех i 
j; i, j =1…n, или можно использовать коэффициент корреляции 
= 
= 
; ковариация в этом случае будет выглядеть таким образом: = 
.
Итак, нужно создать набор долей в наших инвестициях. 
– доля вложения в бумагу №1, а 
… 
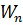доля вложений в бумагу №n. Сумма этих
долей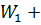 
… 
= 1, либо
Например, наша задача получить доходность от инвестиции в среднем размере Rn; а значит, равна она Rn = 
+…+ 
; либо
Цель – создать минимальный риск, для этого 
= 
= 
+ 
+ + 
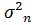* min, либо
= 
+…+ 
+ 
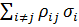
min.
В математике это носит название поиск условного экстремума.
Допустим, есть доходность 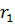=10% и 
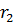=20%, желаемая прибыль 15%.
У нас есть система уравнений 
Подставляем 
– это система линейных алгебраических уравнений.
Используя метод вычислений, когда из первого уравнения вычитают второе уравнение 10 раз, получим такой ответ:
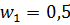
Ответ: при и 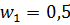доход составит 15%.
Мы можем получить и 12% дохода.
Ответ: при и доход составит 12%.
Когда мы берем только 
, а 
= 0, значит 0*10+1*20 = 20.
Получить дохода больше 20% тоже можно.
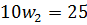
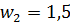
- получило отрицательное значение, что может быть в действительности. Это называют – иметь «открытую позицию».
Метод Марковица заключается в том, что нужно найти экстремум (в нашем случае минимум) имеющих n переменных и нужно найти е минимум ƒ(
… 
) min.
Когда речь идет о min безусловном, то min находится следующим образом: вычисляются частные производные по ( … )
Это необходимые условия гладкой функции (для min и для max). Но в нашем примере не безусловный экстремум, а с определенными условиям:
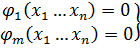m<n
Эта задача в формулировке Лагранжа, решается так:
L ( … , 
, 
… 
) = ƒ( … ) + 
min
1. Необходимо посчитать частные производные от этой функции и производные по λ.
+ 
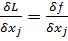; j=1…n,
= 
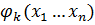; k=1;m.
Если все частные производные прировнять к 0, получим систему уравнений, имеющих n+m переменных. Решением будет являться min нашей функции Лагранжа и одновременно условным min ƒ( … ).
В «роли» переменных выступают: 
и в роли ƒ( … ) выступает дисперсия портфеля: = = 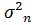+ + + * min
Итак ƒ(
= 
+ 
- стремится к min при следующих условиях:
Функция Лагранжа для задачи Марковица:
L = (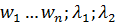
) = 
+ 
+ 
+ 
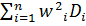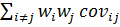min
Считаем производные
+ 
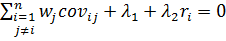; i = 1…n.
0;
.
Итак, получается система уравнений.
Методов решения этой системы уравнения много, продемонстрируем решение этого уравнения с помощью матрицы.
* 
= 
Матричная форма записи системы линейных алгебраических уравнений.
Пример умножения матрицы
; 
* 
Единичные матрицы (Е) – Это диагональная матрица (по диагонали всегда 1). Если умножить матрицу А на единичную матрицу Е, то в ответе будет матрица А.
Обратные матрицы Аˉ¹. Если Аˉ¹ *А=Е.
Решение уравнения
x = 4; y = 3
Проверяем
