Задача 9. Задано распределение:
| Fi | |||||||
| Хi |
Найти его коэффициенты асимметрии и эксцесс через нормированные моменты 3 и 4 порядка. Построить график распределения.
Варианты к задаче 6, 8 и 9
| Fi | ||||||||
| Хi | ||||||||
ТЕМА 6. ПОКАЗАТЕЛИ КОНЦЕНТРАЦИИ И ДИФФЕРЕНЦИАЦИИ
Задача 10. Дано распределение объектов по имущественному признаку.
| ОТ | |||||
| ДО | |||||
| Частота |
Найти значение первого и девятого дециля.
Варианты к задаче 10
| от | ||||||
| до | ||||||
Задача 11. Денежные доходы населения составляют:
| Социальная группа населения | Доли населения | Денежные доходы в тыс. дол. в год. |
| 1. | 0,18 | |
| 2. | 0,18 | |
| 3. | 0,24 | |
| 4. | 0,30 | |
| 5. | 0,10 |
Построить Кривую Лоренца, найти коэффициенты Лоренца и Джини.
Варианты к задаче 11
| Варианты | Денежные доходы в тыс. дол. в год. | ||||
ТЕМА 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОДЕЙСТВИЙ. СЛУЧАЙ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
Задача 12. Заданы пары значений бинарного признака.
| ДА | НЕТ | |
| ДА | ||
| НЕТ |
Найти значения коэффициента Фехнера и фи квадрат 
Варианты к задаче 12
| Вари ант | ||||||||||
| Количество обследований | ||||||||||
| Вариант | ||||||||||
| Количество обследований |
ТЕМА 8. ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПРИЗНАКАМИ. КОРРЕЛЯЦИОННАЯ СВЯЗЬ
Задача 13. Даны значения величин 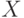 и
и 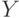 .
.
| X | ||||||||||
| Y |
Найти коэффициент линейной корреляции.
Задача 14. Даны значения величин 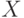 и
и 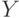 .
.
| X | ||||||||||
| Y |
Найти коэффициент линейной корреляции.
ТЕМА 9. РАНГОВЫЕ КОЭФФИЦИЕНТЫКОРРЕЛЯЦИИ
Задача 15. Даны значения величин 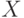 и
и 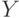 .
.
| X | ||||||||||
| Y |
Найти коэффициенты корреляции К. Спирмэна и М. Кендэла
ТЕМА 10. УРАВНЕНИЕ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Задача 16. Даны значения величин 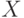 и
и 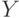 .
.
| X | ||||||||||
| Y |
Найти коэффициенты уравнения линейной регрессии:
ТЕМА 11. АНАЛИЗ РЯДОВ ДИНАМИКИ.
АВТОКОРРЕЛЯЦИЯ В РЯДАХ ДИНАМИКИ
Задача 17. Даны значения величин 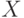 и
и 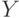 .
.
| X | ||||||||||
| Y |
Найти коэффициент автокорреляции, автокорреляцию в остатках, критерий Дарбина–Уотсона.
Задача 18. На основе данных задачи 16. Найти коэффициент корреляции Y с ее предыдущим значением Х = Х-1; найти коэффициенты уравнения регрессии Y с ее предыдущим значением Х = Х-1; найти остаточную дисперсию регрессии Y с предыдущим значением Х = Х-1; найти остаточное среднее квадратичное отклонение регрессии Y с ее предыдущим значением Х = Х-1; определить автокорреляцию.
Задача 19. На основе данных задачи 16. Найти коэффициент корреляции Y с ее предыдущим значением Х = Х-2; найти коэффициенты уравнения регрессии Y с ее предыдущим значением Х = Х-2; найти остаточную дисперсию регрессии Y с предыдущим значением Х = Х-2; найти остаточное среднее квадратичное отклонение регрессии Y с ее предыдущим значением Х = Х-2; определить автокорреляцию.
Варианты к задачам 13-19
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y | |||||||||||
| X | |||||||||||
| Y |
ТЕМА 12. ДЕМОГРАФИЧЕСКАЯ СТАТИСТИКА
Задача 20. Известно распределение населения по возрастам, вероятности смерти (Рм) и обзаведения ребенком (Pb).
| Px | Pb | Численность (тыс.) | ||
| 0,05 | ||||
| 0,08 | ||||
| 0,1 | ||||
| 0,1 | 1,5 | |||
| 0,25 | 1,5 | |||
| 0,35 | ||||
| 0,40 | ||||
| 0,55 | ||||
| 0,75 | ||||
| -------- |
Найти численность населения в возрасте старше 50 лет через 30 лет. Оценить изменение за каждые 10 лет демографическую нагрузку.
ТЕМА 13. СТАТИСТИЧЕСКИЕ ИНДЕКСЫ
Задача 21. Товарооборот в базисном и отчетном периодах. Найти индексы Ласпейреса, Пааше и Фишера.
| qo | po | q1 | p1 | |
| A | ||||
| B | ||||
| C |